Algebraic Aspects of Topological Quantum Computing Eric Rowell

Algebraic Aspects of Topological Quantum Computing Eric Rowell Indiana University

Collaborators Z. Wang (IU and MS Research*) M. Larsen (IU) R. Stong (Rice) * “Project Q” with M. Freedman, A. Kitaev, K. Walker and C. Nayak

What is a Quantum Computer? Any system for computation based on quantum mechanical phenomena Create Manipulate Measure Quantum Systems

Classical vs. Quantum • Bits {0, 1} 1 • Qubits: V=C 2 1 (superposition) 0 • Logical Operations on {0, 1}n • Unitary Operations on V X n • Deterministic: output unique • Probabilistic: output varies (Uncertainty principle) a 0

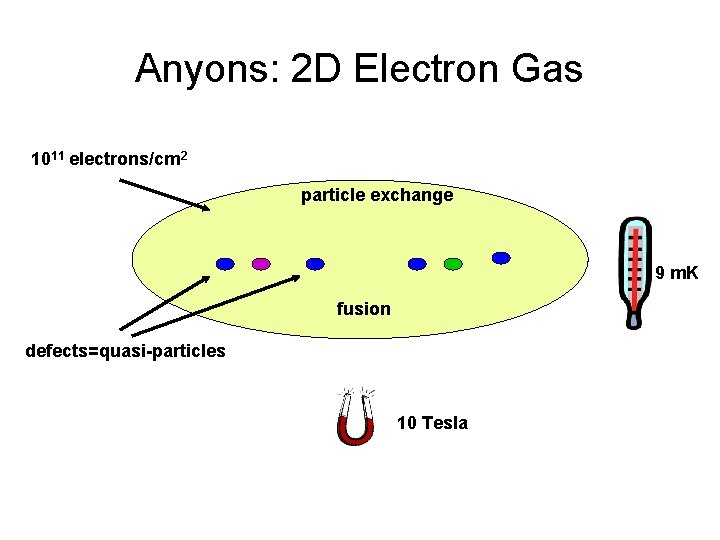
Anyons: 2 D Electron Gas 1011 electrons/cm 2 particle exchange 9 m. K fusion defects=quasi-particles 10 Tesla

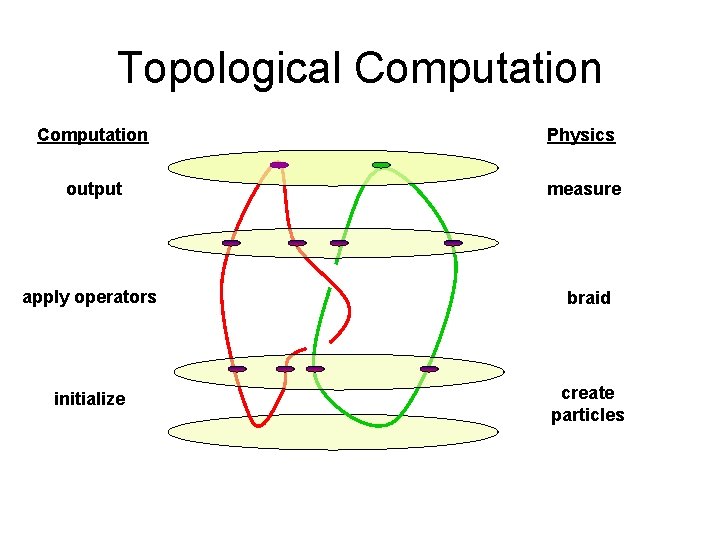
Topological Computation Physics output measure apply operators braid initialize create particles

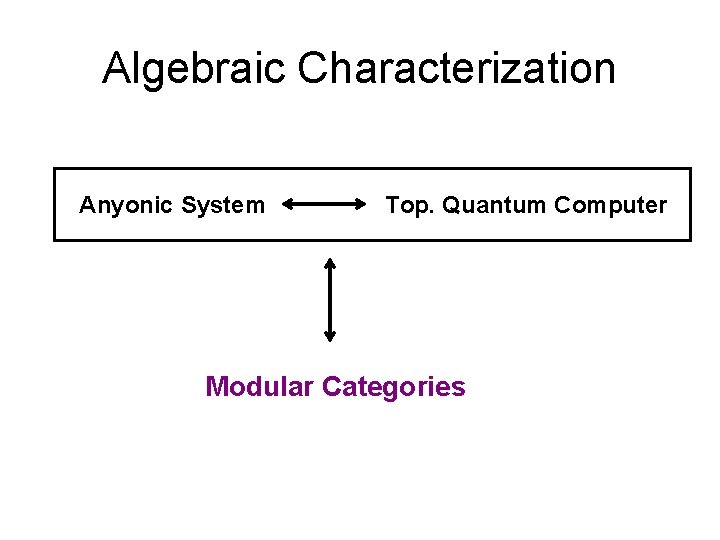
Algebraic Characterization Anyonic System Top. Quantum Computer Modular Categories

Toy Model: Rep(G) • Irreps: {V 1=C, V 2, …, Vk} • Sum V + W, product V X W, duals W* • Semisimple: every W= + mi. Vi • Rep: Sn End. G(V X n)

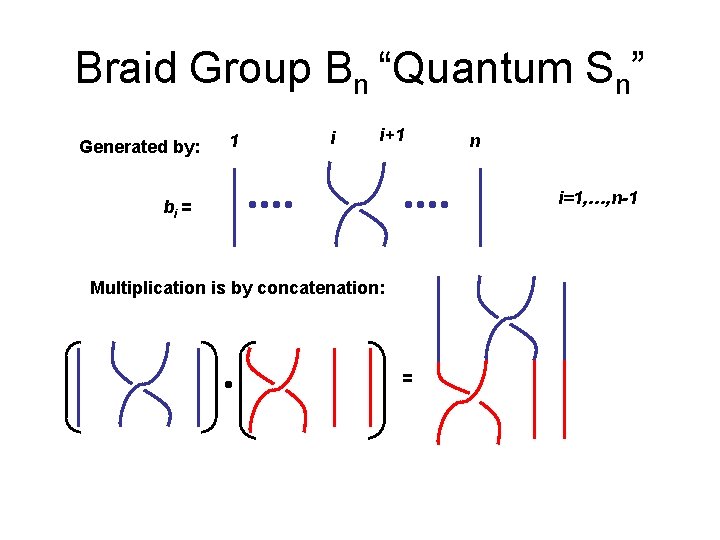
Braid Group Bn “Quantum Sn” Generated by: 1 i i+1 n i=1, …, n-1 bi = Multiplication is by concatenation: =

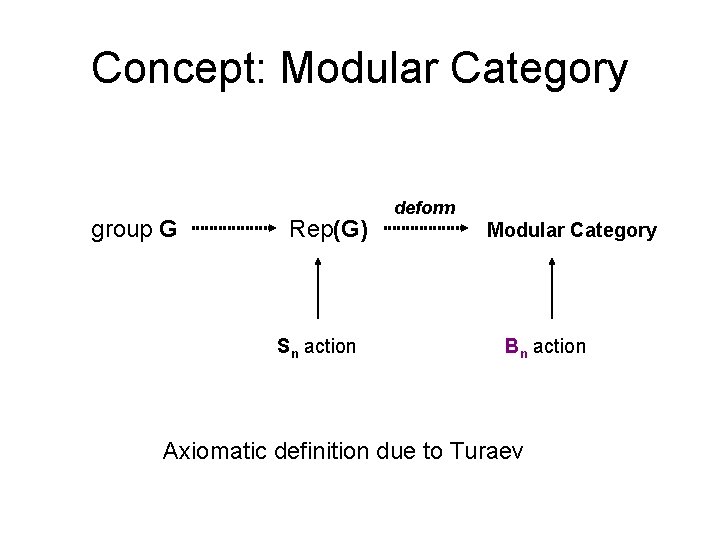
Concept: Modular Category group G Rep(G) Sn action deform Modular Category Bn action Axiomatic definition due to Turaev

Modular Category • Simple objects {X 0=C, X 1, …XM-1} + Rep(G) properties • Rep. Bn End(X X n) (braid group action) • Non-degeneracy: S-matrix invertible

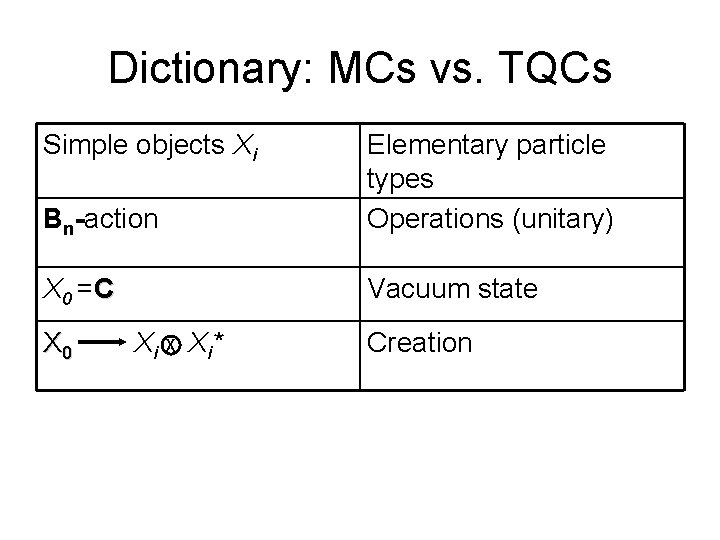
Dictionary: MCs vs. TQCs Simple objects Xi Bn-action Elementary particle types Operations (unitary) X 0 =C Vacuum state X 0 X i X X i* Creation

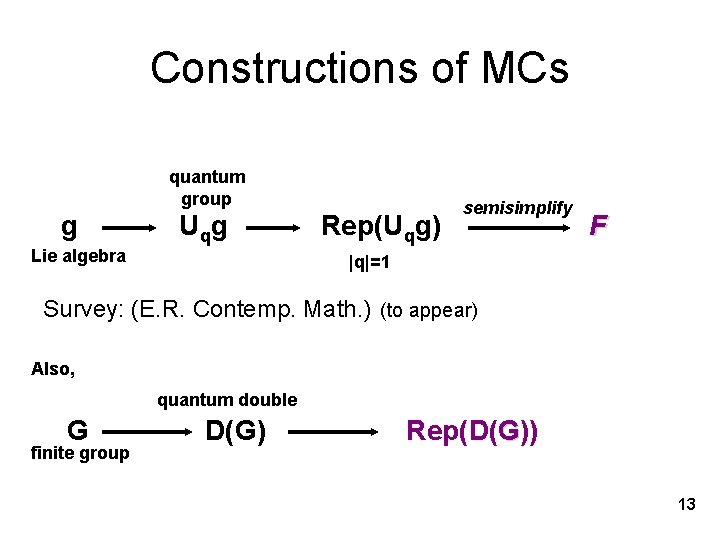
Constructions of MCs quantum group g U qg Lie algebra Rep(Uqg) semisimplify F |q|=1 Survey: (E. R. Contemp. Math. ) (to appear) Also, quantum double G finite group D(G) Rep(D(G)) 13

Physical Feasibility Realizable TQC Bn action Unitary Uqg Unitarity results: (Wenzl 98), (Xu 98) & (E. R. 05)

Computational Power Physically realizable {Ui} universal if all {Ui} = { all unitaries } TQC universal F(Bn) dense in Pk. SU(k) Results: in (Freedman, Larsen, Wang 02) and (Larsen, E. R. , Wang 05) Physical Hurdle: Realizable as Anyonic Systems?

Classify MCs 1 -1 Recall: distinct particle types Simple objects in MC Conjecture (Z. Wang 03): The set { MCs of rank M } is finite. Classified for: M=1, 2 (V. Ostrik), 3 and 4 (E. R. , Stong, Wang) True for finite groups! (Landau 1903)

Groethendieck Semiring • Assume X=X*. For a MC D: Xi X Xj = + Nijk Xk • Semiring Gr(D): =(Ob(D), + , X ) • Encoded in matrices (Ni)jk : = Nijk

Modular Group • Non-dengeneracy S symmetric • Compatibility T diagonal • 1 1 0 1 T, 0 -1 1 0 S give a unitary projective rep. of SL(2, Z)

Our Approach • Study Gr(D) and reps. of SL(2, Z) • Ocneanu Rigidity: Finite-to-one MCs {Ni} • Verlinde Formula: {Ni} determined by S-matrix

Some Number Theory • Let pi(x) = det(Ni - x. I) and K = Split({pi}, Q). • Study Gal(K/Q): always abelian! • Nijk integers, Sij algebraic, constraints polynomials.

Sketch of Proof (M<5) 1. Show: 1 Gal(K/Q) SM 2. Use Gal(K/Q) + constraints to determine (S, {Ni}) 3. For each S find T rep. of SL(2, Z) 4. Find realizations.

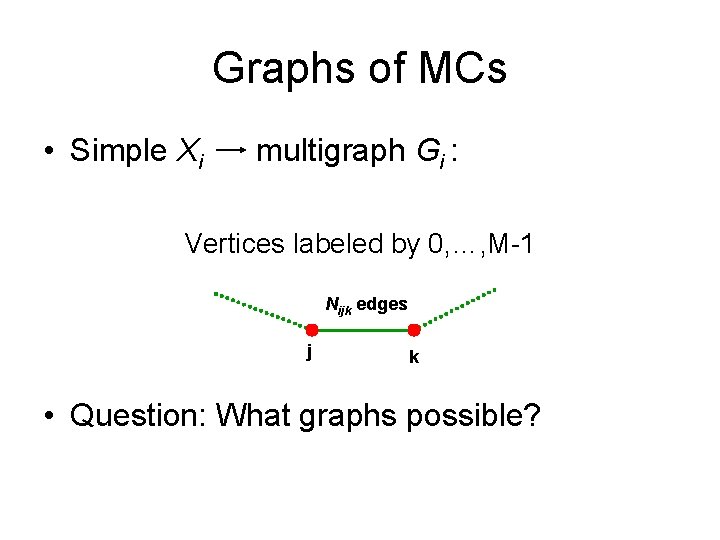
Graphs of MCs • Simple Xi multigraph Gi : Vertices labeled by 0, …, M-1 Nijk edges j k • Question: What graphs possible?

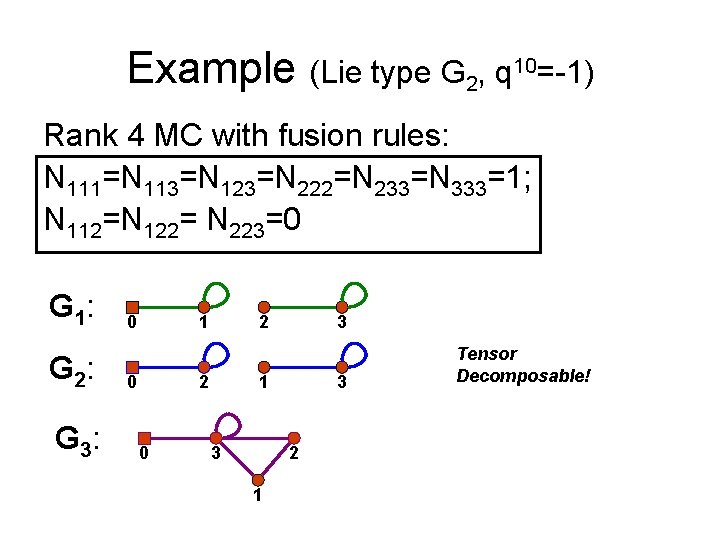
Example (Lie type G 2, q 10=-1) Rank 4 MC with fusion rules: N 111=N 113=N 123=N 222=N 233=N 333=1; N 112=N 122= N 223=0 G 1: G 2: G 3: 0 1 0 2 2 0 3 1 3 3 2 1 Tensor Decomposable!

Classification by Graphs Theorem: (E. R. , Stong, Wang) Indecomposable, self-dual MCs of rank<5 are classified by:

Future Directions • Classification of all MCs • Prove Wang’s conjecture • Images of Bn reps… • Connections to: link/manifold invariants, Hopf algebras, operator algebras…

Thanks!