Algebraic Algorithms Definition Combinatorial methods Tries to construct

Algebraic Algorithms

Definition Combinatorial methods: Tries to construct the object explicitly piece-by-piece. Algebraic methods: Implicitly sieves for the object by evaluating a sum.

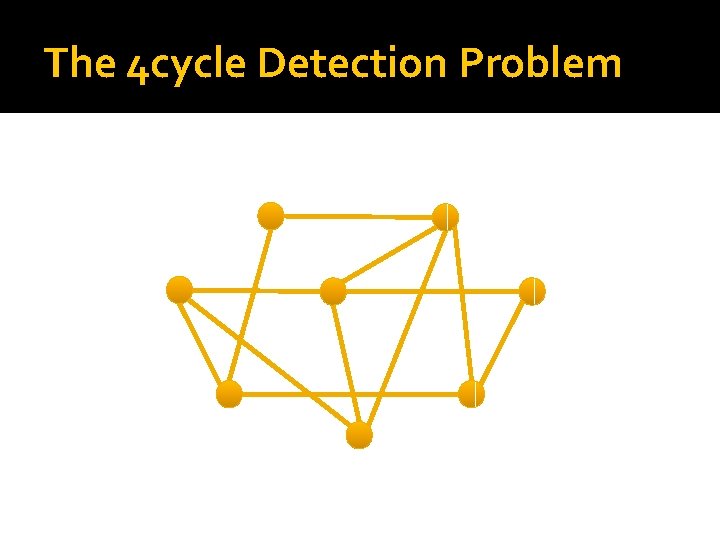
The 4 cycle Detection Problem

4 cycle detection 1. 2. 3. 4. 5. 6. 7. 8. Init a boolean nxn table T(: , : )=false. For each vertex v For each pair of neighbors u, w of v If T(u, w) then return true and stop T(u, w)=true End Return false

The Triangle Detection Problem

Square Matrix Multiplication �What is the computational complexity in terms of number of scalar operations (*, +) of computing the product of two nxn-matrices A and B? �From definition Cij=Sk Aik. Bkj we get O(n 3) time. �There is a (highly theoretical) O(n 2. 373) time algorithm!

Strassen’s algorithm

Strassen’s algorithm T(n)=cn 2+7 T(n/2)=cn 2+7 c(n/2)2+72 T(n/4)= cn 2+7 c(n/2)2+72 c(n/4)2+73 T(n/8)=…= cn 2(1+7/4+(7/4)2+…+(7/4)log 2(n))+7 log 2(n)= O(nlog 2(7))=O(n 2. 81).

Verifying Matrix Products �Given three nxn matrices A, B, and C you want to verify that AB=C. �Can you do this faster than recomputing the matrix product?

Verifying Matrix Products �Idea: Project the difference matrix on a randomly chosen 0/1 -vector r. �If (AB-C)r=A(Br)-Cr=0, we conclude that AB=C, otherwise we deem them different. �No false negatives. �False positives with probability <=1/2. Note that this is an O(n 2) time algorithm!

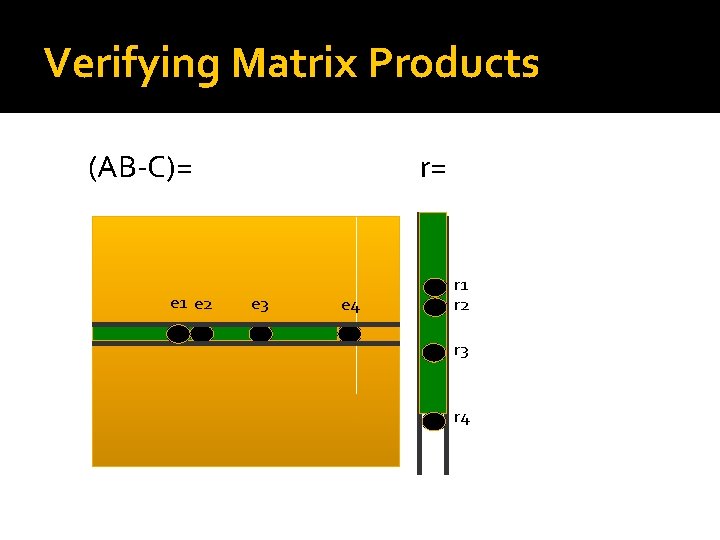
Verifying Matrix Products (AB-C)= e 1 e 2 r= e 3 e 4 r 1 r 2 r 3 r 4

Polynomial Identity Testing �Given ”black box” multivariate polynomial P, is P identically zero or not? �Think of polynomial P as given by arithmetic circuit: + x + + + x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14

The Schwartz Zippel Lemma �Schwartz-Zippel Lemma: Let P(x 1, x 2, …, xn) be a multivariate non-zero polynomial of total degree d over a finite field F. For uniformly and independently sampled values r 1, r 2, …, rn in F:

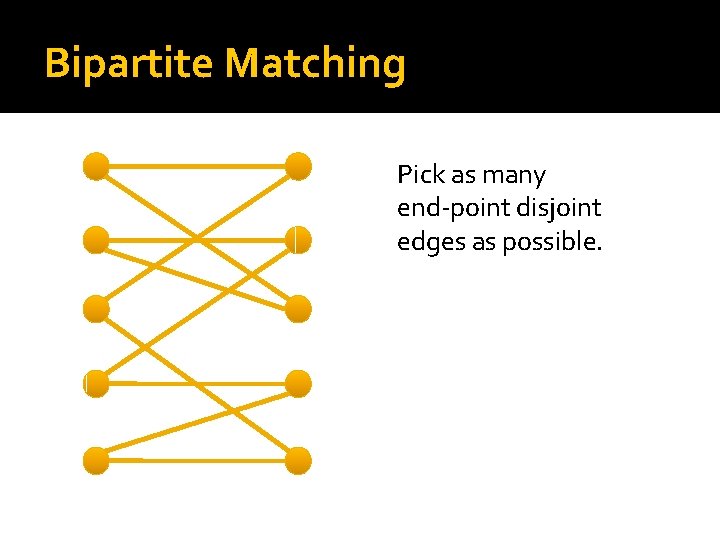
Bipartite Matching Pick as many end-point disjoint edges as possible.

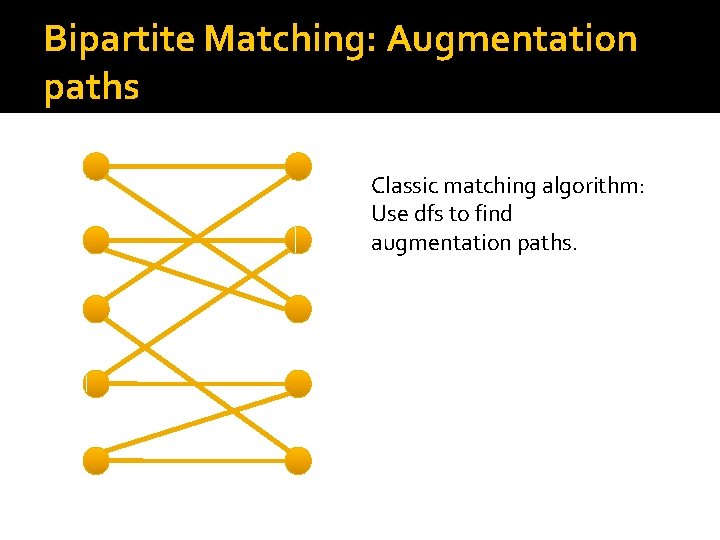
Bipartite Matching: Augmentation paths Classic matching algorithm: Use dfs to find augmentation paths.

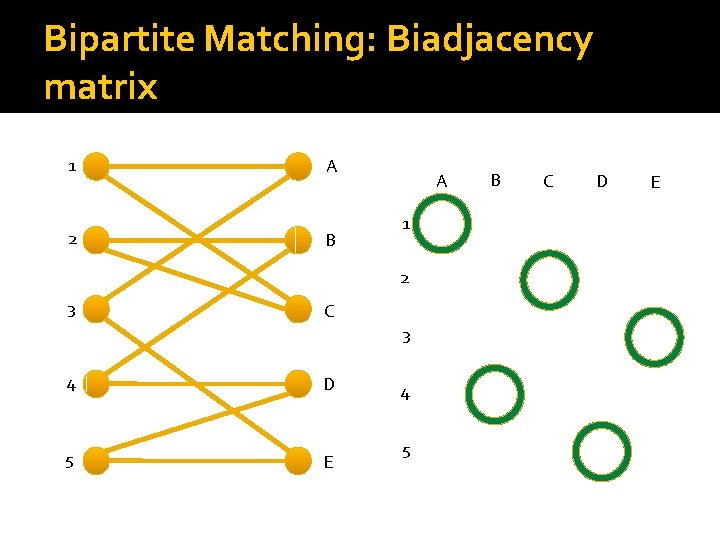
Bipartite Matching: Biadjacency matrix 1 2 A B A 1 2 3 C 3 4 5 D E 4 5 B C D E

Determinants A 1 In fields of characteristic two: 2 3 4 5 B C D E

Fields of characteristic two F 4 + 0 1 A B * 0 1 A B 0 0 0 1 1 0 B A 1 0 1 A B A A B 0 1 A 0 A B 1 B B A 1 0 B 1 A

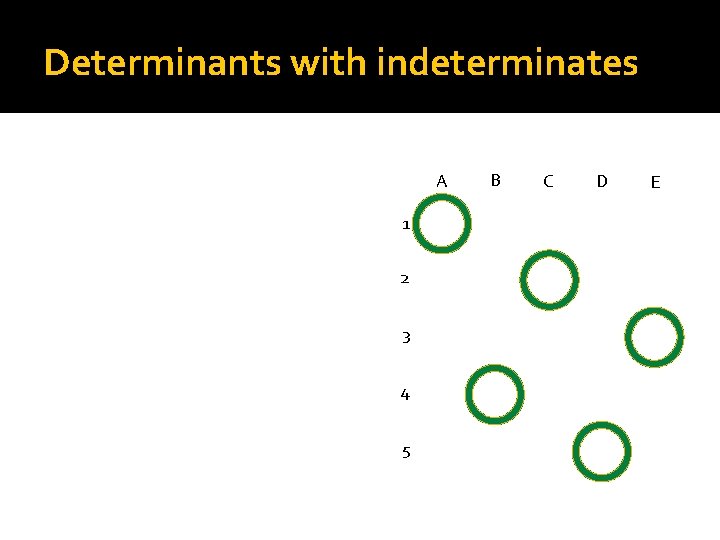
Determinants with indeterminates A 1 2 3 4 5 B C D E

Algorithm 1. Replace indeterminates by random values xij=rij. 2. Compute the determinant. 3. If it is non-zero return Yes otherwise No. A 1 2 3 4 5 B C D E

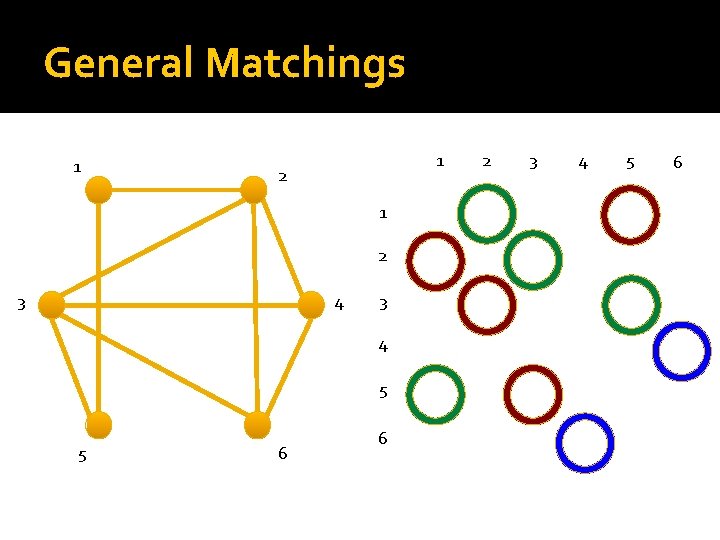
General Matchings 1 1 2 3 4 5 5 6 6 2 3 4 5 6