Algebra Where letters are numbers and numbers are

Algebra Where letters are numbers and numbers are letters!
Algebra Concepts Geometric Sequencing FOIL Method Expressions as Statements Evaluating and Simplifying Expressions One Step Linear Equations Two Step Linear Equations Inequalities Slopes, Intercepts and Graphing Functions Quadratic Equations Monomials

Geometric Sequencing • You can use differences to find the patterns of some sequences • Patterns may be shown using shapes or numbers

Geometric Sequencing Examples What is the next term in the sequence 5, 15, 3, 53, 81…. The pattern is adding 6 more to the previous number added The next term would be…. 115, 155 Refer to packet for 2 nd example

Geometric Sequencing Examples • What are the next 2 terms of the sequence 3, 5, 8, 12…. • The pattern is adding one more than previous number added • The next two terms are 17 and 23

Assignments • Complete the 1 st worksheet, I will come around and help • Tomorrow you are to complete the other 2 • On the 3 rd worksheet #’s 8 -14 are extra credit, they are a little more difficult

Expressions as Statements • You can write a word equation to represent relationships before writing an algebraic equation. – For example: If the larger number is increased by the smaller, the result is 84 – 3 x + 20 + x = 84

Expressions as Statements Examples 9 less than the product of 6 and 8 9 - (6 x 8) Twice a number, increased by 10 2 x + 10 If a number is decreased by 9 and the difference is multiplied by 3, the result is the same as twice the number decreased by 10 3(x- 9) = 2 x – 10

Expressions as Statements Examples • Find the number (from previous example) 3(x – 9) = 2 x – 10 3 x – 27 + 10= 2 x – 10 + 10 3 x – 17 = 2 x 3 x – 17 – 3 x= 2 x – 3 x -17 = -1 x -1 -1 17 = x

Assignments • Complete the 2 worksheets that follow the examples page in the packet • 1 st worksheet match the expression with its statement • 2 nd worksheet write an expression to go with the equation

FOIL Method • Foil stands for First: Multiply the first term in each set of parentheses Outer: Multiply the outer term in each set of parentheses Inner: Multiply the inner term in each set of parentheses Last: Multiply the last term in each set of parentheses

FOIL Method Example • (3 + 7 x) (6 + 2 x) • First: 3 x 6 = 18 • Outer: 3 x 2 x = 6 x • Inner: 7 x x 6 = 42 x • Last: 7 x x 2 x = 14 x² • After completing with FOIL Method • 18 + 6 x + 42 x + 14 x² Or 18 + 48 x + 14 x²

Assignments • Complete the 3 practice problems on the FOIL Method sheet in your packet

Evaluating & Simplifying Equations • A variable is used as a placeholder in an algebraic expression. Examples are x, y, a, and so on • A term is a number, a variable, or the product of numbers and variables. For example – 2, x, and 5 y • A coefficient is the numerical factor in a term, for example the – 2 in – 2 z

Evaluating & Simplifying Expressions • Like terms are terms that have the same variable. For example 3 z and 7 z • The simplest form of an algebraic expression is the form of the expression after all like terms have been combined 3 x + 7 x= 10 x would be the simplest form
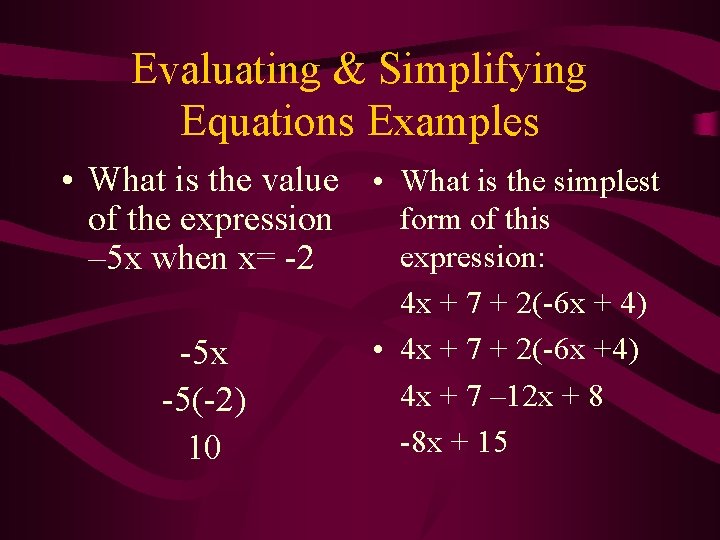
Evaluating & Simplifying Equations Examples • What is the value • What is the simplest form of this of the expression: – 5 x when x= -2 -5 x -5(-2) 10 4 x + 7 + 2(-6 x + 4) • 4 x + 7 + 2(-6 x +4) 4 x + 7 – 12 x + 8 -8 x + 15

Evaluating & Simplifying Equations Worksheet Examples From Worksheet #1 1. 3 a – d = 3(4) – (-3) 12 + 3 = 15 2. 2 c + 5 b = 2(5) + 5(-2) 10 – 10= 0 3. 6(c + d)= 6 ( 5 + (-3)) 6(5 -3)= 6(2)=12

Evaluating & Simplifying Equations Worksheet Examples Worksheet #2 1. 11 c + 5 d – 6 c + 2 c 7 c +5 d 5. 8(-4 b + 2 d) – 12 d + 2 b 3. 7(2 n-3 r)-8 r 14 n-21 r-8 r 14 n-29 r 7. 12 f – 6 g – 12 g – 7 f 5 f – 18 g -32 b + 16 d – 12 d +2 b -30 b +4 d

Assignments • Complete the practice on the back of the worksheet with the examples on it • When you finish with that complete # 4, 8, 12, and 18 on worksheet #1, and # 2, 4, 6, & 8 on the 2 nd worksheet

One Step Linear Equations • An equation is a number sentence with two expressions that are equal. • An equation with a variable is an open sentence. • When you solve an equation you find the value of the variable that makes the open sentence (original equation) true.

One Step Linear Equations • To solve an equation means to get the variable alone on one side of the equals sign. • Use inverse operations to “take an equation apart” – Addition and subtraction are inverse operations – Multiplication and division are inverse operations

One Step Linear Equations Examples • What is the solution to x-8 = -3 to x-8 + 8= -3 + 8 2 z= -10 x = 5 2 2 • What is the solution to z= -5 m/4 = 8 m/4 (4) = 8 (4) m = 32

One Step Linear Equations Examples • b – 9 = 21 b – 9 + 9 = 21 + 9 b = 30 • r + 17 = -5 r + 17 – 17 = -5 – 17 r = -22 12 + c = 55 12 + c – 12 = 55 – 12 c = 43 •

Assignments • On worksheet # 1 complete problem #’s 4 -12 • We will complete the rest of the worksheets through an activity/game

Two Step Linear Equations • When an equation requires more than one operation, first undo addition or subtraction, then multiplication or division • Parentheses in an equation can be removed by using the distributive property – 2(x – 3) + 5= 15 – 2 x- 6 + 5 = 15

Solving Two Step Equations • When an equation has the variable on both sides of the equals sign get the variable terms on one side and the numerical terms on the other side • • • 2 x-7=5 x-19 2 x-7+7=5 x-19+7 2 x=5 x-12 2 x-5 x=5 x-5 x-12 -3 x=-12 -3 -3 x=4

Two Step Linear Equations Examples • 2 n + 3=9 2 n + 3 – 3= 9 -3 2 n= 6 2 2 n= 3 • 7(x + 2) – 10=14 7 x + 14 – 10 = 14 7 x +4 – 4 = 14 -4 7 x = 10 7 7 x= 10/7= 1 3/7

Two Step Linear Equations Examples • 2 x – 7 = 5 x – 19 2 x – 7 + 19 = 5 x – 19 + 19 2 x + 12 = 5 x 2 x + 12 – 2 x = 5 x – 2 x 12=3 x 3 3 4=x

Assignments • Complete the practice on the back of the page • We will complete the other worksheet through an activity

Inequalities • You can solve an inequality the same way you solve an equation – The exception is that you must reverse the inequality symbol when you multiply or divide by a negative number • In an inequality, two quantities are related in on of these ways – Less than <, less than or equal to <, greater than >, and greater than or equal to >

Inequalities • The solution set for inequalities can contain many values (more than one answer) • To graph the solution set use a number line

Inequalities Examples • What is the solution set for –z + 1 < 5 – -z +1 – 1 < 5 – 1 – -z < 4 • What is the solution set for 2 k – 3 > 15 – 2 k – 3 + 3 > 15 + 3 – 2 k > 18 2 2 – k>9 • Graph the inequality – y < 10 – x>4 • Worksheet #1 numbers 1 & 2

Assignments • Worksheet #1 numbers 3, 5 and 7 • Worksheet # 2 even numbers • We will do worksheet #3 as a class activity

Slope, Intercepts, & Graphs

Slope, Intercepts, and Graphs Examples

Assignments

Functions

Functions Examples

Assignments

Quadratic Equations

Quadratic Equations Examples

Assignments

Monomials

Monomial Examples

Assignments
Algebra Review Geometric Sequencing Expressions as Statements Evaluating & Simplifying Statements One Step Linear Equations Two Step Linear Equations Inequalities Slope, Intercepts, and Graphs Functions Quadratic Equations Monomials
- Slides: 46