Algebra What is the difference between 5 x

Algebra What is the difference between 5 x² + 4 x – 7 and 5 x² + 4 x – 7 = 0 3 x + 7 y + 8 4 a + 2 b – 6 a + 2 ab + 3 Cant simplify -2 a + 2 b + 2 ab + 3 6 x + 6 x² - 12 x + 6 x³ 14 x – 7 – 4 + 2 x -6 x + 12 x² 16 x – 11 4 m + 3 mn – 6 n – m + 4 n 3 m + 3 mn – 2 n All of these are expressions. Simplify the above expressions

Brackets Multiply out the brackets and simplify the expressions (4 x + 5)(3 x – 2) 4 x(3 x – 2) + 5(3 x – 2) 12 x² - 8 x + 15 x – 10 12 x² + 7 x – 10 (3 x – 3)(4 x – 4) 3 x(4 x – 4) – 3(4 x – 4) 12 x² - 12 x – 12 x + 12 12 x² - 24 x + 12 (2 x – 6)(4 x – 1) 2 x(4 x – 1) - 6(4 x – 1) 8 x² - 2 x - 24 x + 6 8 x² - 26 x + 6 (5 x + 2)(3 x – 4) 5 x(3 x – 4) + 2(3 x – 4) 15 x² – 20 x + 6 x – 8 15 x² - 14 x – 8

Substitution If a = 4, b = 3 and c = -2, find the value of the following: (i) 3 a + 4 b 3(4) + 4(3) 12 + 12 = 24 (ii) 4 b – 2 a 3(3) – 4(4) 9 – 16 = -7 (iii) 2 ab – 3 a (iv) 5 b + 3 c (v) 3 a – 2 c (vi) 2 a – 3 bc 5(3) + 3(-2) 15 – 6 =9 3(4) – 2(-2) 12 + 4 = 16 2(4) – 3(3)(-2) 8 + 18 = 26 2(4)(3) – 3(4) 24 – 12 = 12

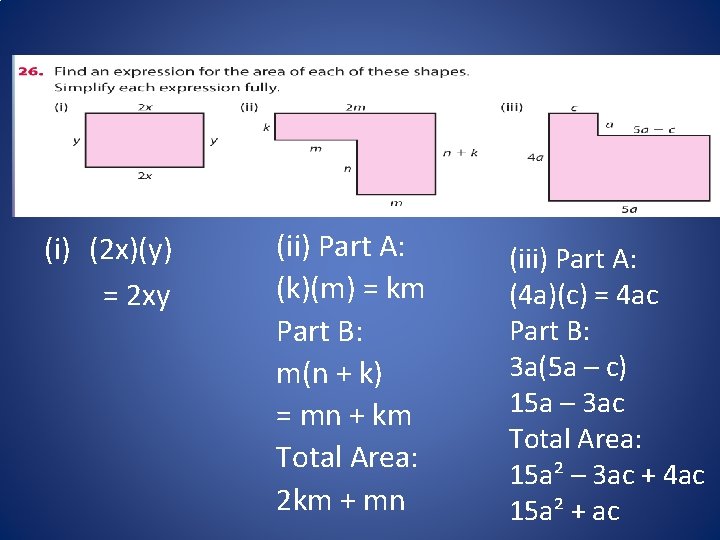
(i) (2 x)(y) = 2 xy (ii) Part A: (k)(m) = km Part B: m(n + k) = mn + km Total Area: 2 km + mn (iii) Part A: (4 a)(c) = 4 ac Part B: 3 a(5 a – c) 15 a – 3 ac Total Area: 15 a² – 3 ac + 4 ac 15 a² + ac

Homework (i) d(d + 5) = d² + 5 d (i) 5 p x 2 q = 10 pq (ii) 2 n(n - 8) = 2 n² - 8 n (ii) 3 m x 7 n = 21 mn (iii) 3 a² x 3 b = 9 a²b (ii) 3 p(5 - p) = 15 p - 3 p² (iv) 5 x² x 2 y² = 10 x²y² (ii) 5 k(4 + k) = 20 k + 5 k² (v) 3 cd² x 5 c² = 15 c³d² (vi) 4 v²w x 7 vw³ = 28 v³w⁴

Forming Expressions Simple expression: “The school wants to buy a number of computers for the school. If one computer costs € 450 then come up with an expression to represent the cost of ANY amount of computers” n = number of computers C = total cost of computers Expression: C = 450 n eg. if the school decides to by 19 computers? n = 19 C = 450(19) C = 8550

“The school has a deal with the manufacturers that no matter how many computers they buy they will install them in the school for € 340” Come up with a new expression for this information Original Expression: C = 450 n New Expression: C = 450 n + 340 “If the school buys 26 computers what will the total cost be? ” C = 450(26) + 340 C = 11700 + 340 C = € 12040

Two Variables “A school decides to send some of their students to an Irish college for a weekend. Unfortunately it is a sexist Irish college and they charge € 24 for each boy and € 29 for each girl” Come up with an expression for finding the total cost for the school. Number of boys = b Number of girls = g Total Cost = C “They also have to hire a bus which costs € 300 for the trip” “They finally decide on bringing 13 boys and 17 girls” Find the total cost. C = 24 b + 29 g + 300 b = 13 g = 17 C = 24(13) + 29(17) + 300 C = 312 + 493 + 300 C = € 1105

“A girl has gotten a new “bill pay” mobile phone. Every text message she sends cost 13 c and her phone calls cost 33 c per minute. Also there is a standing charge of € 15 every month. ” Come up with a general expression to help calculate the total bill. B = Total Bill t = no. of texts c = no. of call minutes B = 13 t + 33 c + 1500 What is the total bill in June if she sends 256 texts and spends 27 mins on the phone? B = 13(256) + 33(27) + 1500 B = 3328 + 891 B = 5719 c = € 57. 19 What if they charge VAT at 25% on the total bill? € 57. 19 x 125% = € 71. 49 Now we want an expression to include the VAT. . 125% = ¹²⁵⁄₁₀₀ = ⁵⁄₄ B = ⁵⁄₄(13 t + 33 c + 1500) Calculate her bill for July if she sends 312 texts and spends 19 mins on the phone t = 312 c = 19 B = ⁵⁄₄(13(312) + 33(19) + 1500) B = ⁵⁄₄(4056 + 627 + 1500) B = ⁵⁄₄(6183) B = 7728. 75 c = € 77. 29

Where else would this be used? Biology Bacteria Cell Division: “If each cell divides into 2 in every 2 minutes how many cells will exist after 20 minutes? ” After 2 min: 2 cells How many cells will you have after After 4 mins: 4 cells 2½hours? ? After 6 mins: 8 cells Time (t) = 150 mins After 8 mins: 16 cells Rate (r)= 2 every 2 mins = ln 2/2 After 10 mins: 32 cells Initial No. of Cells (IC) = 1 cell Expression: After 12 mins: 64 cells No. of Cells after t mins = IC(ert) After 14 mins: 128 cells Cells after 2. 5 hrs = 1(e(ln 2/2)(150) ) After 16 mins: 256 cells C = 3. 78 x 10²² After 18 mins: 512 cells NB: DONT WORRY IF YOU DON’T After 20 mins: 1024 cells FOLLOW THIS!! I JUST THOUGHT IT WOULD BE INTERESTING TO DO!!!

Exercise (i) 5 x + 12 = 22 5 x + 12 – 12 = 22 – 12 5 x = 10 5 5 x=2 (ii) 2 x – 8 = 4 2 x – 8 + 8 = 4 + 8 2 x = 12 2 2 x=6 (iv) 5 x – 6 = 4 x – 11 5 x – 6 + 6 = 4 x - 11 + 6 5 x = 4 x - 5 5 x - 4 x = 4 x - 4 x – 5 x = -5 (vi) 6 x – 13 = 3 x + 5 (iii) 2 x + 15 = 3 2 x + 15 – 15 = 3 – 15 2 x = -12 2 2 x = -6 (v) 4 x + 8 = 3 x – 5 4 x + 8 – 8 = 3 x - 5 – 8 4 x = 3 x - 13 4 x - 3 x = 3 x - 3 x – 13 x = - 13 (vii) 9 x + 15 = 22 – 5 x

(vi) 6 x – 13 = 3 x + 5 Ctd 6 x – 13 + 13 = 3 x + 5 + 13 6 x = 3 x + 18 6 x - 3 x = 3 x - 3 x + 18 3 x = 18 3 3 x=6 (vii) 9 x + 15 = 22 – 5 x 9 x + 15 – 15 = 22 – 5 x – 15 9 x = 7 – 5 x 9 x + 5 x = 7 – 5 x + 5 x 14 x = 7 14 14 x=½

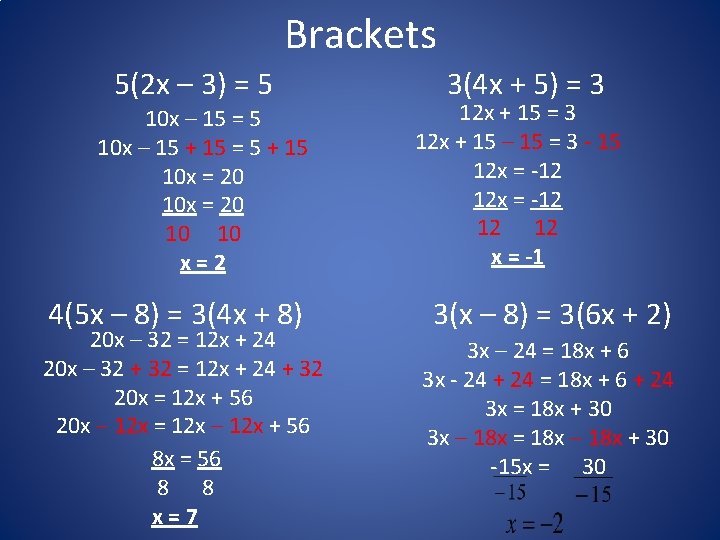
Brackets 5(2 x – 3) = 5 10 x – 15 + 15 = 5 + 15 10 x = 20 10 10 x=2 4(5 x – 8) = 3(4 x + 8) 20 x – 32 = 12 x + 24 20 x – 32 + 32 = 12 x + 24 + 32 20 x = 12 x + 56 20 x – 12 x = 12 x – 12 x + 56 8 x = 56 8 8 x=7 3(4 x + 5) = 3 12 x + 15 – 15 = 3 - 15 12 x = -12 12 12 x = -1 3(x – 8) = 3(6 x + 2) 3 x – 24 = 18 x + 6 3 x - 24 + 24 = 18 x + 6 + 24 3 x = 18 x + 30 3 x – 18 x = 18 x – 18 x + 30 -15 x = 30

Equations (i) Length of both sides: 2 x + 2 and 10 – 2 x Both sides are the same length. . 2 x + 2 = 10 – 2 x 2 x + 2 – 2 = 10 – 2 x – 2 2 x = 8 – 2 x 2 x + 2 x = 8 – 2 x + 2 x 4 x = 8 x=2 (ii) 3 x + 3 = 13 – 2 x 3 x + 3 – 3 = 13 – 2 x – 3 3 x = 10 – 2 x 3 x + 2 x = 10 – 2 x + 2 x 5 x = 10 5 5 x=2

Homework Q 1 - 3 page 10 Look at the next few questions on this page and have an idea on how you will do them

Groupwork – page 10

Helen = x (years old) If Helen is x, then Ann is x + 3 Sum of their ages = x + (x + 3) = 2 x + 3 2(2 x + 3) = 50 4 x + 6 – 6 = 50 – 6 4 x = 44 x = 11 (how can you check your answer?

(i) Perimeter is adding the sides together. . x + 2 x + 1 + 3 x Perimeter = 6 x + 1 (ii) Perimeter = 55 6 x + 1 – 1 = 55 – 1 6 x = 54 x=9

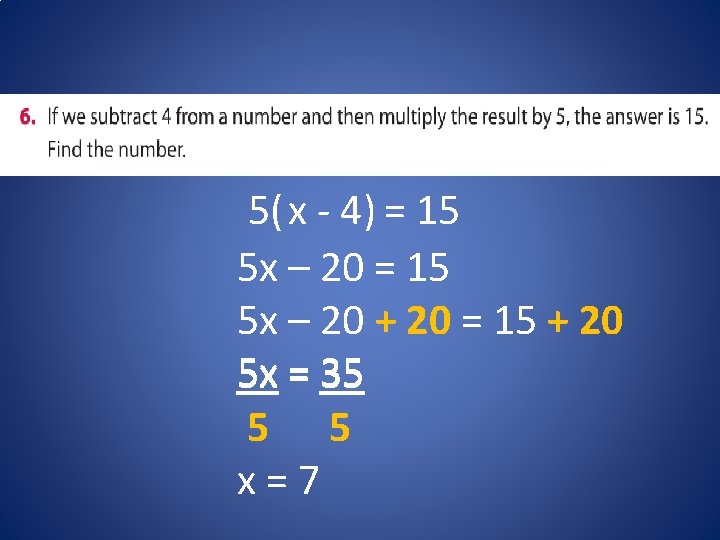
5( x - 4) = 15 5 x – 20 + 20 = 15 + 20 5 x = 35 5 5 x=7

2(x + 4)= x + 20 2 x + 8 – 8 = x + 20 – 8 2 x = x + 12 2 x – x = x – x + 12 x = 12

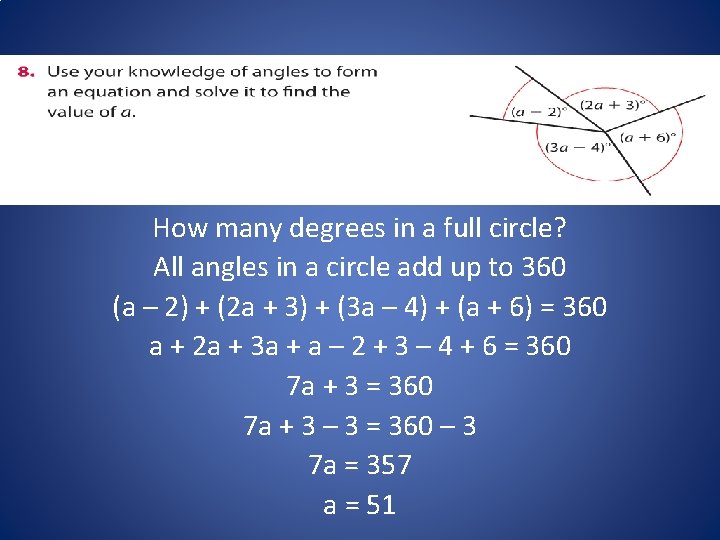
How many degrees in a full circle? All angles in a circle add up to 360 (a – 2) + (2 a + 3) + (3 a – 4) + (a + 6) = 360 a + 2 a + 3 a + a – 2 + 3 – 4 + 6 = 360 7 a + 3 – 3 = 360 – 3 7 a = 357 a = 51

(i) What x + 1 is+ special x + 2 x = 63 a about 4 x + square? 3 = 63 width 4 x +Length 3 – 3 == 63 – 3 x 4 x= =3060– 2 x x + 2 xx==30 15– 2 x + 2 x 3 x = 30 x = 10 (ii) Perimeter of triangle: x + 1 + x + 2 x 4 x + 3 Perimeter of Rectangle: x + 30 – 2 x - 2 x + 60 If they are the same: 4 x + 3 = -2 x + 60 4 x + 3 – 3 = - 2 x + 60 – 3 4 x + 2 x = -2 x + 57 6 x = 57 6 6 x = 9½

Number Systems (revision) Natural Numbers (N) “Whole, positive numbers” eg. 1, 2, 3, 5, 100, 12234 Integers (Z) “Whole numbers, both positive numbers” eg. -1, - 11, 22, 32, -102, 1432. Real Numbers “Every imaginable number” eg. 1, 4, 2½, 4. 783, - 12. 98, - 432. 01,

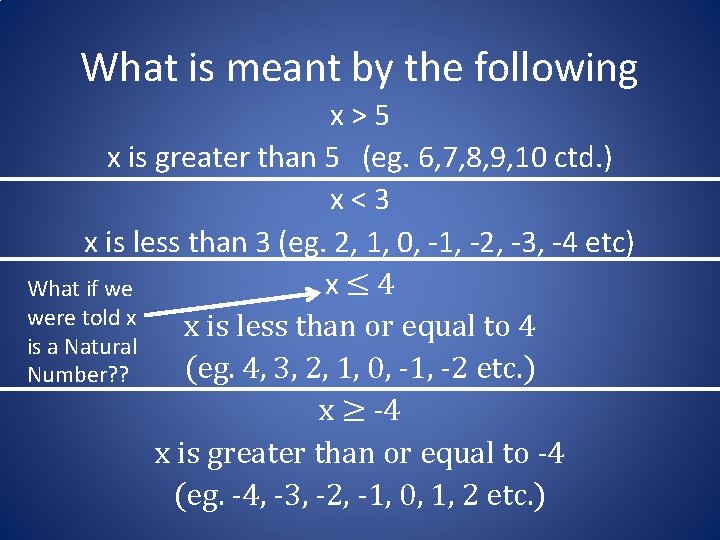
What is meant by the following x>5 x is greater than 5 (eg. 6, 7, 8, 9, 10 ctd. ) x<3 x is less than 3 (eg. 2, 1, 0, -1, -2, -3, -4 etc) x≤ 4 What if we were told x x is less than or equal to 4 is a Natural (eg. 4, 3, 2, 1, 0, -1, -2 etc. ) Number? ? x ≥ -4 x is greater than or equal to -4 (eg. -4, -3, -2, -1, 0, 1, 2 etc. )

Number Lines Plot the following on a number line x ≥ 1, -9 -8 -7 -6 -5 -4 -3 -2 -1 xЄN 0 x ≤ 6, -9 -8 -7 -6 -5 -4 -3 -2 -1 -8 -7 -6 -5 -4 -3 -2 2 3 4 5 6 7 8 9 xЄN 0 x ≥ -4, -9 1 1 2 xЄZ -1 0 1 2

Number Lines Plot the following on a number line x ≥ 3, -9 -8 -7 -6 -5 -4 -3 -2 -1 xЄZ 0 x ≤ 6, -9 -8 -7 -6 -5 -4 -3 -2 -1 -8 -7 -6 -5 -4 -3 -2 2 3 4 5 6 7 8 9 xЄR 0 x ≥ -4, -9 1 1 2 xЄR -1 0 1 2

Inequalities Spot the difference Solve the following equation: Solve the following inequality: 6 x – 7 ≤ 11 where x Є Z. 6 x – 7 = 11 Plot your answer on a number line 6 x – 7 + 7 = 11 + 7 6 x – 7 ≤ 11 6 x = 18 6 x – 7 + 7 ≤ 11 + 7 6 x/ = 18/ 6 6 6 x ≤ 18 x=3 6 x/ ≤ 18/ 6 6 x≤ 3 x ≤ 3, -5 -4 -3 -2 -1 xЄZ 0 1 2 3 4 5

5 Exercise 7. 2 x + 5 ≤ 1 2 x + 5 – 5 ≤ 1 – 5 2 x ≤ -4 x ≤ -2 xЄZ -4 -3 -2 -1 0 1 12. 2 x + 2 ≤ 8 2 x + 2 – 2 ≤ 8 – 2 2 x ≤ 6 x≤ 3 xЄR 2 3 4 5 -5 -4 -3 -2 -1 0 1 2 3 4 5

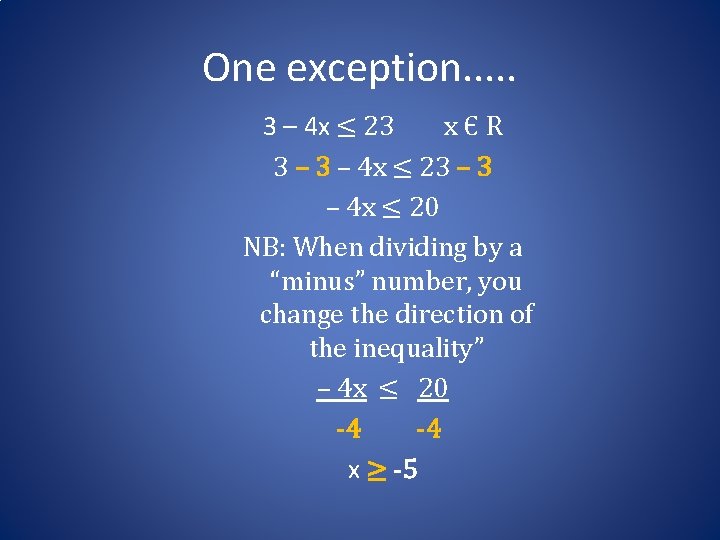
One exception. . . 3 – 4 x ≤ 23 xЄR 3 – 4 x ≤ 23 – 4 x ≤ 20 NB: When dividing by a “minus” number, you change the direction of the inequality” – 4 x ≤ 20 -4 -4 x ≥ -5

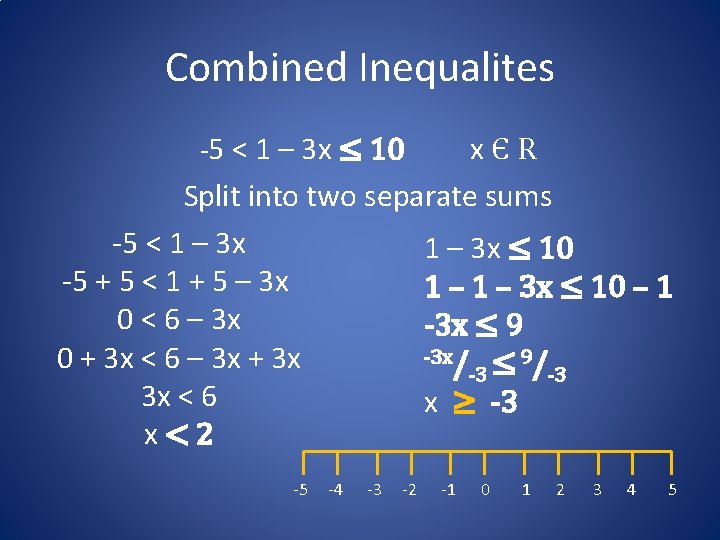
Combined Inequalites -5 < 1 – 3 x ≤ 10 xЄR Split into two separate sums -5 < 1 – 3 x ≤ 10 -5 + 5 < 1 + 5 – 3 x 1 – 3 x ≤ 10 – 1 0 < 6 – 3 x -3 x ≤ 9 -3 x/ ≤ 9/ 0 + 3 x < 6 – 3 x + 3 x -3 -3 3 x < 6 x ≥ -3 x<2 -5 -4 -3 -2 -1 0 1 2 3 4 5

Solve the following (i) 6 x + 18 = 3 x – 6 6 x + 18 – 18 = 3 x – 6 – 18 7 < 3 x – 2 and 3 x 3 x –– 22 ≤ ≤ 13 13 6 x = 3 x – 24 7 < 3 x – 2 6 x – 3 x = 3 x – 24 7 + 23 x< =3 x- – 242 + 2 3 x/9 < -24/ 3 x = 3 3 9/ < 3 x/5 x – 4 ≤ 16 x 3 = -8 3 x xЄR (iii) 3 x – 43><22 3 x – 4 + 4 > 22 + 4 3 x – 2 + 3 x 2 ≤>13 26+ 2 > 26/3 3 x 3 x≤/315 x =58⅔ x≤ < x–≤ 25≤ 13 (v) 7 <33 x (ii) 3 x – 12 = 7 x + 12 3 x 7 x +5 x 12––+4412 ≤ -9 –≤ 12 5 x +– 12 4 =and 5 x ≤ 16 16 3 x =-97 x + 24 < 5 x – 4 6 x – 7 x = 7 x – 7 x + 24 -9 + 4 < 5 x – 4 + 4 -4 x = 24 -4 x/ 5=<245 x /-4 -4 5/ < 5 x/ x =5 -6 5 1<x xЄZ (iv) 5 – 9 x ≤ 23, 5 - 5 – 9 x > 23 – 5 5 x-9 x – 4>+18 4 ≤ 16 + 4 -9 x/ 5 x 18 ≤/-920 > -9 x < -2 x≤ 4 1 <≤x 5 x ≤ 4– 4 < 16 (vi) -9

(i) Between 350 and 500? 350 < c < 500 (ii) 300 350 400 350 500 (iii) Inclusive? 120 ≤ x ≤ 200 (iv) 120 140 160 180 200 (v) 550 ¹⁄₁₀ of 120? = 12 ¹⁄₁₀ of 200? = 20 12 ≤ x ≤ 20

Problem Solving Crossing the railway bridge story? ? Steps: 1. Identifying the Problem 2. What do we know? 3. Use of skills/past knowledge 4. Experimentation 5. Success!

(i)(iii) Perimeter = xwe + 1 know + x + 2 x What do Perimeter = 4 x + 3 about squares? Length. Perimeter = Width = 63 4 x + 3 = 63 Length = x 4 x + 3 – 3 = 63 – 3 Width = 30 – 2 x 4 x = 60 x =x 30 – 2 x = 15 x + 2 x = 30 – 2 x + 2 x 3 x = 30 x = 10 (ii) Perimeter of Triangle = 4 x + 3 Perimeter of Rect. = 30 – 2 x + x + x Perimeter of Rect. = 60 – 2 x Per. of Triangle = Per. of Rectange 4 x + 3 = 60 – 2 x 4 x + 3 – 3 = 60 – 3 – 2 x 4 x = 57 – 2 x 4 x + 2 x = 57 – 2 x + 2 x 6 x = 57 6 x/ = 57/ 6 6 x = 9. 5

x+3 18 + x x + 23 18 + x + 23 = 57 2 x + 41 – 41 = 57 – 41 2 x = 16 x=8 2 x (4 x + 5) – (3 x + 2) 4 x + 5 – 3 x – 2 x+3+x– 3 = 2 x 4 x + 5 + 2 x = 35 6 x + 5 – 5 = 35 – 5 6 x = 30 x=5

(i) x + B = 20 Get B on it’s own? x – x + B = 20 – x (ii) x + C = 15 x – x + C = 15 – x (iii) B + C = 19 20 – x + 15 – x = 19 35 – 2 x = 19 – 35 -2 x = -16 x=8

Area of Irregular Shape (3)(x) = 3 x (2 x)(3) = 6 x Total Area = 9 x Area of White Part 2(x + 2) 2 x + 4 Area of Pink section 9 x – (2 x + 4) 9 x – 2 x – 4 Area of shaded section = 7 x – 4 (iii) Area of shaded section = 38 7 x – 4 + 4 = 38 + 4 7 x = 42 x=6

(i) If she was 20 years old. . . 6 years ago she would be. . . 20 – 6 = 14 If she is x years old. . 6 years ago she would be x– 6 (ii) In 12 years time her age will be: x + 12 3 times x – 6 ? 3(x – 6) 3 x – 18 x + 12 = 3 x – 6 x + 12 – 12 = 3 x – 6 – 12 x = 3 x – 18 x – 3 x = 3 x – 18 -2 x = -18 -2 x/ = -18/ -2 -2 x=9

women = x Men = x – 8 Children = x + 30 Total = 166 x + x – 8 + x + 30 = 166 3 x + 22 – 22 = 166 – 22 3 x = 144 x = 48 There are 48 women Check your answer? women = x = 48 Men = x – 8 = 40 Children = x + 30 = 78 48 + 40 + 78 = 166

Sea Travel = x Train = x – 120 Plane = x – 120 – 80 Total = 10 hrs 40 mins Total Time = 640 mins Total = x + x – 120 – 80 Total Time = 3 x – 320 = 640 3 x – 320 + 320 = 640 + 320 3 x = 960 x = 320 Sea Travel = 320 mins (5 hrs 20 mins) Train = 200 mins (3 hrs 20 mins) Plane = 120 (2 hrs)