ALGEBRA TWO CHAPTER TWO LINEAR EQUATIONS AND FUNCTIONS

ALGEBRA TWO CHAPTER TWO: LINEAR EQUATIONS AND FUNCTIONS Section 2. 7 - Piecewise Functions

LEARNING GOALS Goal One - Represent piecewise functions. Goal Two - Use piecewise functions to model real-life quantities.

VOCABULARY • Piecewise functions are represented by a combination of equations, each corresponding to a part of the function. • A step-function has a graph which resembles a set of stair steps. An example of a step function is the greatest integer function. This function is denoted by g(x) = [[x]], where for every real number x, g(x) is the greatest integer less than or equal to x.

Evaluating a Piecewise Function 1. Find which equation to used based on the equations' limits 2. Plug x into the correct equation and solve for f(x)

Evaluating a Piecewise Function PROBLEM: Evaluate f (x) when (a) x = -1, (b) x = 1, and (c) x = 3. f (x) = 2 x + 3, f (x) = 2, f (x) = -x + 1, if x < 0 if 0 < x < 2 if x > 2 SOLUTION Since x = -1 is less than zero, use the first equation. f ( x) = 2 x + 3 f (x) = 2(-1) + 3 f ( x) = 1

Evaluating a Piecewise Function PROBLEM: Evaluate f (x) when (a) x = -1, (b) x = 1, and (c) x = 3. f (x) = 2 x + 3, f (x) = 2, f (x) = -x + 1, if x < 0 if 0 < x < 2 if x > 2 SOLUTION Since x = 1 is more than zero, use the second equation. f ( x) = 2 x + 3 f ( x) = 2 f (-1) = 2(-1) + 3 f (1) = 2 f (-1) = 1

Evaluating a Piecewise Function PROBLEM: Evaluate f (x) when (a) x = -1, (b) x = 1, and (c) x = 3. f (x) = 2 x + 3, f (x) = 2, f (x) = -x + 1, if x < 0 if 0 < x < 2 if x > 2 SOLUTION Since x = 3 is more than two, use third equation. f ( x) = 2 x + 3 f ( x) = 2 f ( x) = - x + 1 f (-1) = 2(-1) + 3 f (1) = 2 f (3) = -(3) + 1 f (-1) = 1 f (3) = -2

Evaluating a Piecewise Function PROBLEM: Evaluate f (x) when (a) x = 5, (b) x = 0, and (c) x = -2. f (x) = x + 1, f (x) = -x - 2, if x > 1 if x < 1 SOLUTION Since x = 5 is more than one, use the first equation. f ( x) = x + 1 f (5) = (5) + 1 f (5) = 6

Evaluating a Piecewise Function PROBLEM: Evaluate f (x) when (a) x = 5, (b) x = 0, and (c) x = -2. f (x) = x + 1, f (x) = -x - 2, if x > 1 if x < 1 SOLUTION Since x = 0 is less than one, use the second equation. f ( x) = x + 1 f ( x) = - x - 2 f (5) = (5) + 1 f (0) = -(0) - 2 f (5) = 6 f (0) = - 2

Evaluating a Piecewise Function PROBLEM: Evaluate f (x) when (a) x = 5, (b) x = 0, and (c) x = -2. f (x) = x + 1, f (x) = -x - 2, if x > 1 if x < 1 SOLUTION Since x = -2 is less than one, use the second equation. f ( x) = x + 1 f ( x) = - x - 2 f (5) = (5) + 1 f (0) = -(0) - 2 f (5) = 6 f (0) = - 2 f ( x) = - x - 2 f (-2) = -(-2) - 2 f (-2) = 0

Graphing Piecewise Functions 1. Find the points where x changes 2. Graph the function in the appropriate areas 3. Check to make sure you draw open dot for < or >, and closed dot for < or >
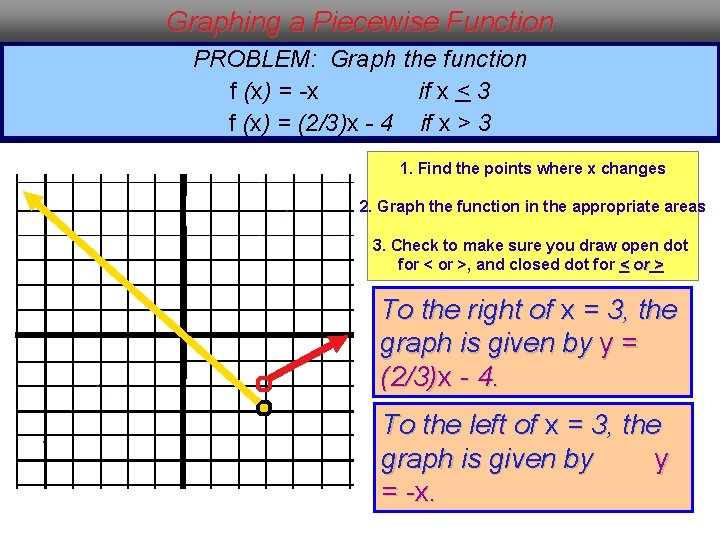
Graphing a Piecewise Function PROBLEM: Graph the function f (x) = -x if x < 3 f (x) = (2/3)x - 4 if x > 3 1. Find the points where x changes 2. Graph the function in the appropriate areas 3. Check to make sure you draw open dot for < or >, and closed dot for < or > To the right of x = 3, the graph is given by y = (2/3)x - 4. To the left of x = 3, the graph is given by y = -x.
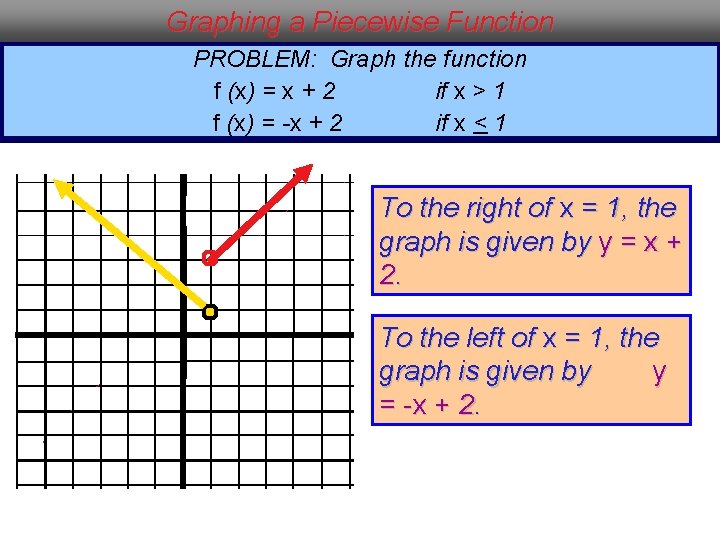
Graphing a Piecewise Function PROBLEM: Graph the function f (x) = x + 2 if x > 1 f (x) = -x + 2 if x < 1 To the right of x = 1, the graph is given by y = x + 2. To the left of x = 1, the graph is given by y = -x + 2.

Graphing a Step Function PROBLEM: Graph the function f (x) = -2 if 0 < x < 2 f (x) = -4 if 2 < x < 4 f (x) = -6 if 4 < x < 6 The graph is composed of three line segments, because the function has three parts. The intervals of x tell you that each line segment is 2 units in length and begins with a solid dot and ends with an open dot.
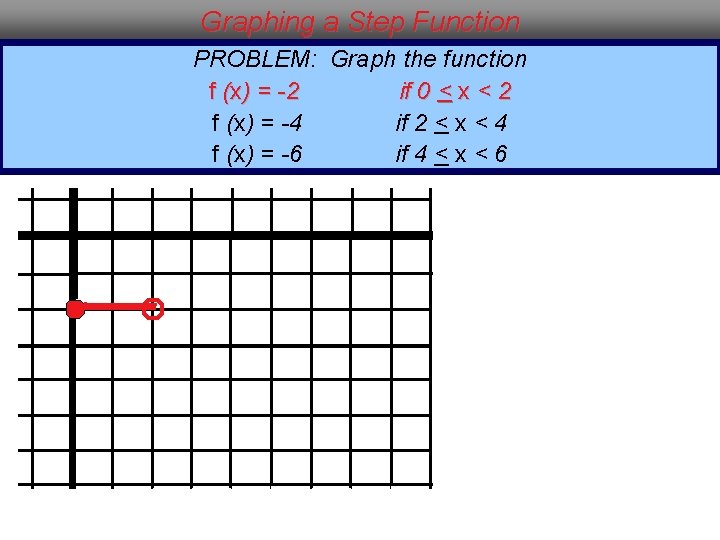
Graphing a Step Function PROBLEM: Graph the function f (x) = -2 if 0 < x < 2 f (x) = -4 if 2 < x < 4 f (x) = -6 if 4 < x < 6
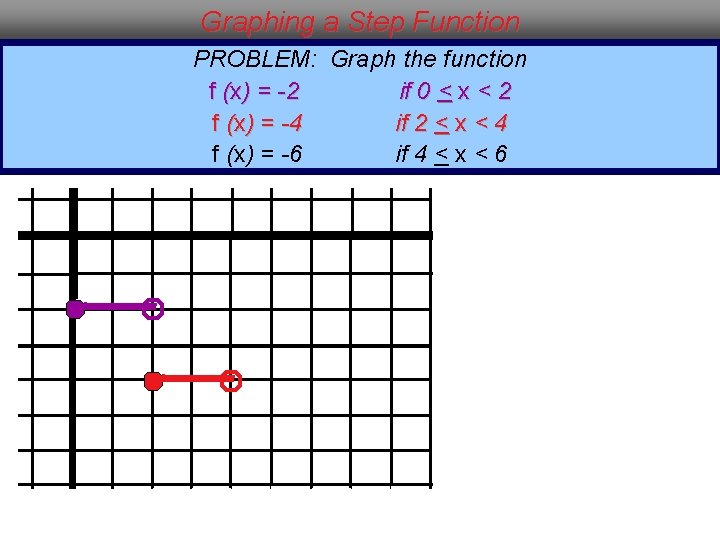
Graphing a Step Function PROBLEM: Graph the function f (x) = -2 if 0 < x < 2 f (x) = -4 if 2 < x < 4 f (x) = -6 if 4 < x < 6
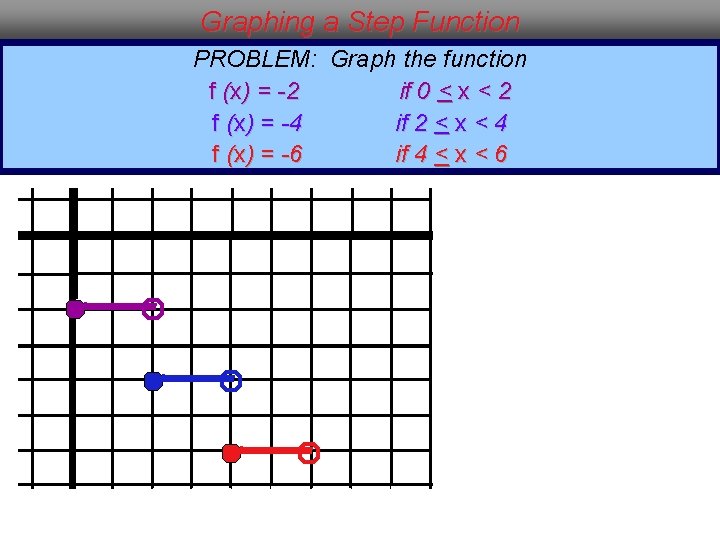
Graphing a Step Function PROBLEM: Graph the function f (x) = -2 if 0 < x < 2 f (x) = -4 if 2 < x < 4 f (x) = -6 if 4 < x < 6

ASSIGNMENT #13, #17, #21, #25, #27, #35 pg. 117 -120.
- Slides: 18