ALGEBRA TWO CHAPTER TWO LINEAR EQUATIONS AND FUNCTIONS

ALGEBRA TWO CHAPTER TWO: LINEAR EQUATIONS AND FUNCTIONS Section 2. 2 - Slope and Rate of Change

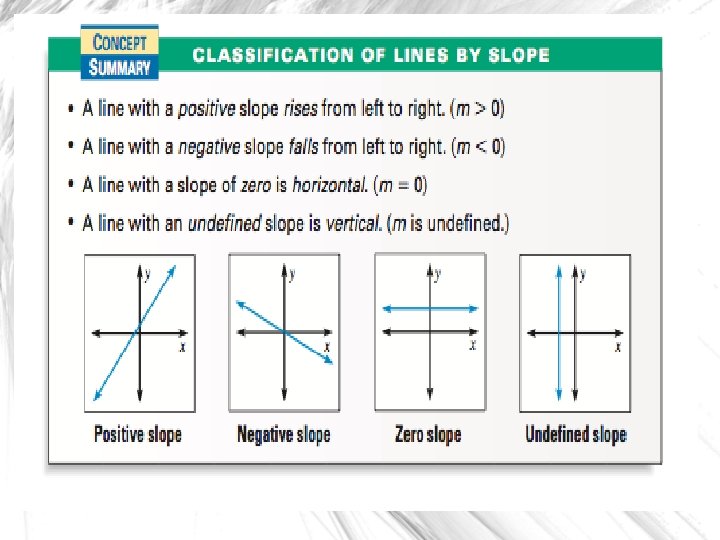
LEARNING GOALS Goal One - Find slopes of lines and classify parallel and perpendicular lines. Goal Two - Use slope to solve real-life problems.

VOCABULARY The slope of a nonvertical line is the ratio of vertical change (the rise) to the horizontal change (the run). The slope of a line is represented by the letter m.

The Slope of a Line The slope of the nonvertical line passing through the points (x 1, y 1) and (x 2, y 2) is: slope=m = (y 2 -y 1) (x 2 - x 1 ) Rise: Difference of y values. Run: Difference of x values.

Finding the slope of a Line PROBLEM: Find the slope of a line passing through (-3, 2) and (1, 5). SOLUTION Let (x 1, y 1) = (-3, 2) and (x 2, y 2) = (1, 5) slope=m = (y 2 -y 1) Rise: Difference of y values. (x 2 -x 1) Run: Difference of x values. = (5 - 2)/(1 -(-3)) = (3)/(1+3) = 3/4 Substitute values. Simplify. Slope is positive. The slope is 3/4. Because the slope is positive, the line rises from left to right.

Finding the slope of a Line PROBLEM: Find the slope of a line passing through (4, 1) and (-6, 3). SOLUTION Let (x 1, y 1) = (4, 1) and (x 2, y 2) = (-6, 3) slope =m= (y 2 -y 1) (x 2 -x 1 ) Rise: Difference of y values. Run: Difference of x values. = (3 - 1)/(-6 -(4)) = (2)/(-10) = -1/5 Substitute values. Simplify. Slope is negative. The slope is -1/5. Because the slope is negative, the line falls from left to right.

Parallel and Perpendicular Lines PARALLEL LINES - The lines are parallel if and only if they have the same slope. Parallel lines NEVER intersect. m 1 = m 2 These two lines have the same slope, but different y-intercepts. They are parallel.

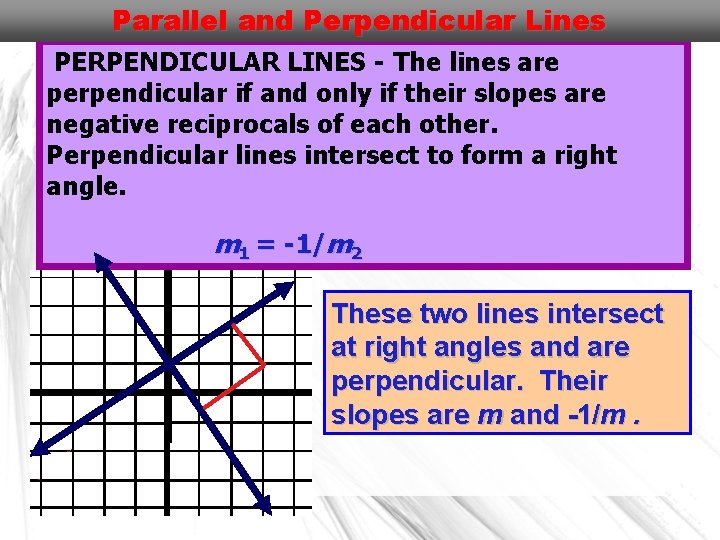
Parallel and Perpendicular Lines PERPENDICULAR LINES - The lines are perpendicular if and only if their slopes are negative reciprocals of each other. Perpendicular lines intersect to form a right angle. m 1 = -1/m 2 These two lines intersect at right angles and are perpendicular. Their slopes are m and -1/m.

Parallel and Perpendicular Lines PROBLEM: Tell whether the lines are parallel, perpendicular, or neither. Line 1: through (-1, 3) and (1, -3) Line 2: through (3, 0) and (0, 1) SOLUTION slope = (y 2 -y 1) (x 2 -x 1 ) Line 1 Rise: Difference of y values. Run: Difference of x values. Line 2 = (-3 -(-1)/(1 -(-1)) = (-3 + 1)/(1 + 1) = (-2)/(2) = -1 = (1 - 0)/(0 - 3) = (1)/(-3) = -1/3

Parallel and Perpendicular Lines PROBLEM: Tell whether the lines are parallel, perpendicular, or neither. Line 1: through (-1, 3) and (1, -3) Line 2: through (3, 0) and (0, 1) SOLUTION These lines are neither parallel or perpendicular. Line 1 = (-3 -(-1)/(1 -(-1)) = (-3 + 1)/(1 + 1) = (-2)/(2) = -1 Line 2 = (1 - 0)/(0 - 3) = (1)/(-3) = -1/3

Parallel and Perpendicular Lines PROBLEM: Tell whether the lines are parallel, perpendicular, or neither. Line 1: through (-2, 6) and (0, -2) Line 2: through (-1, 6) and (1, -2) SOLUTION slope = (y 2 -y 1) (x 2 -x 1 ) Line 1 Rise: Difference of y values. Run: Difference of x values. Line 2 = (-2 - 6)/(0 -(-2)) = (-8)/(1 + 1) = (-8)/(2) = -4 = (-2 - 6)/(1 - (-1)) = (-8)/(2) = -4

Parallel and Perpendicular Lines PROBLEM: Tell whether the lines are parallel, perpendicular, or neither. Line 1: through (-2, 6) and (0, -2) Line 2: through (-1, 6) and (1, -2) SOLUTION These lines are parallel. Line 1 = (-2 - 6)/(0 -(-2)) = (-8)/(1 + 1) = (-8)/(2) = -4 Line 2 = (-2 - 6)/(1 - (-1)) = (-8)/(2) = -4

Slope as Rate of Change PROBLEM: Six years ago a house was purchased for $89, 000. This year it was appraised at $125, 000. Find the average rate of change and use it to determine the value after nine years. SOLUTION Average rate of change = (change in value) / (change in time) = ($125, 000 - $89, 000)/6 years = $36, 000/6 years = $6, 000 per year Over a 9 -year period, the value changed 9 • $6, 000/yr. The value after nine years was $89, 000 + $54, 000 = $143, 000.

Homework Pg 79 -80 #17, 23, 27, 29, 37, 39, 41, 43, 51