Algebra through the Lens of Functions Quadratic Patterns

Algebra through the Lens of Functions Quadratic Patterns 1

Introducing Quadratic Functions

Prior Knowledge ● ● ● Exploration of linear patterns Creating and interpreting graphs of linear functions Critical points of a linear function Understanding of a variable and constant Rate of change of a linear function
Prior Knowledge Exploration of linear patterns: ● ● Expressions Equivalence Distribution Multiple Representations
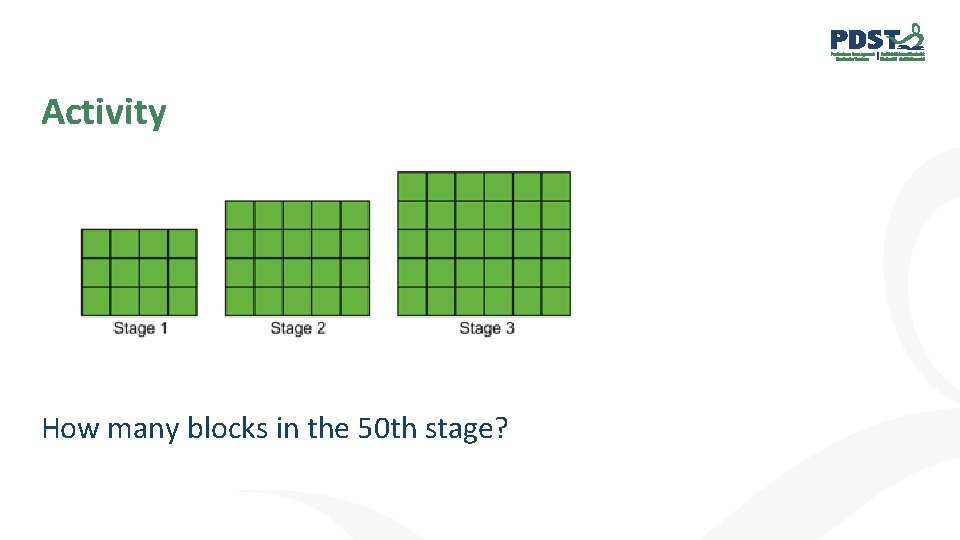
Activity How many blocks in the 50 th stage?
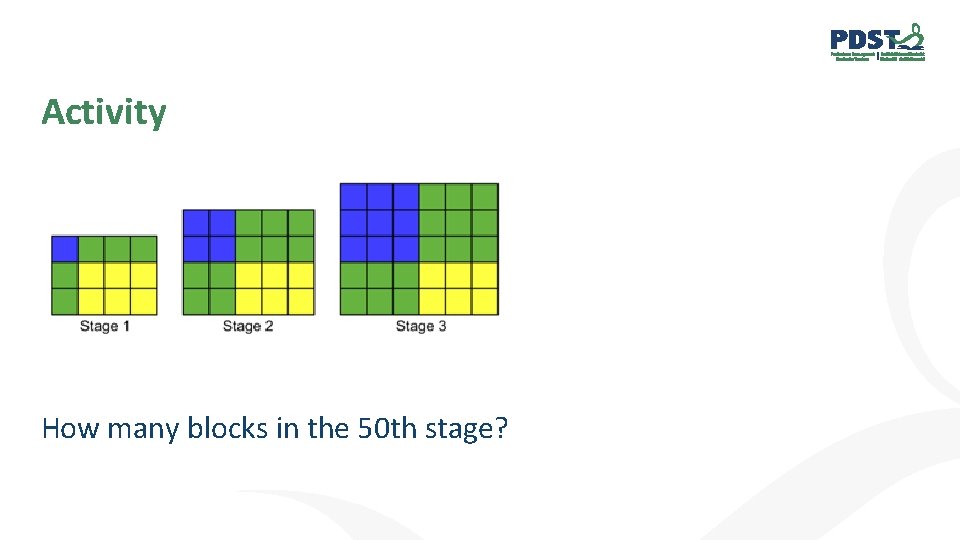
Activity How many blocks in the 50 th stage?
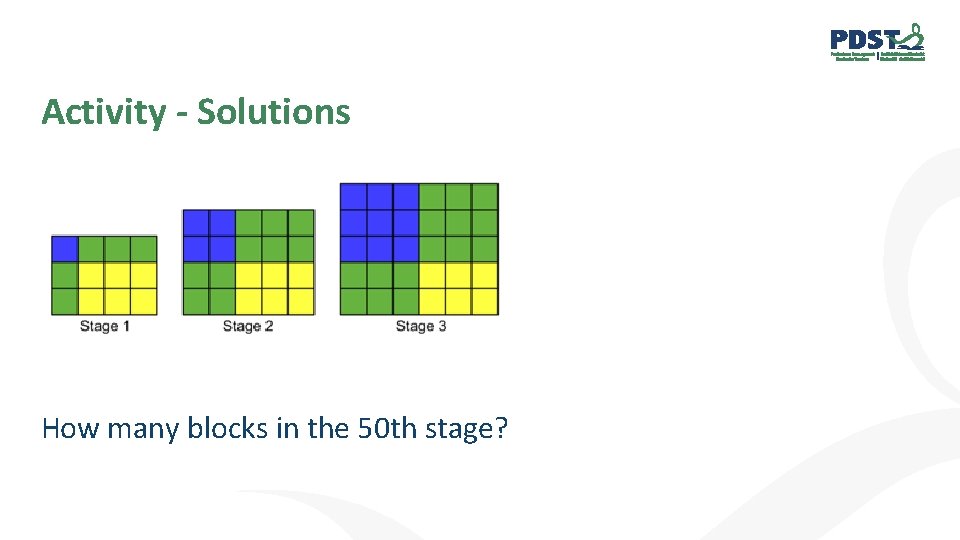
Activity - Solutions How many blocks in the 50 th stage?
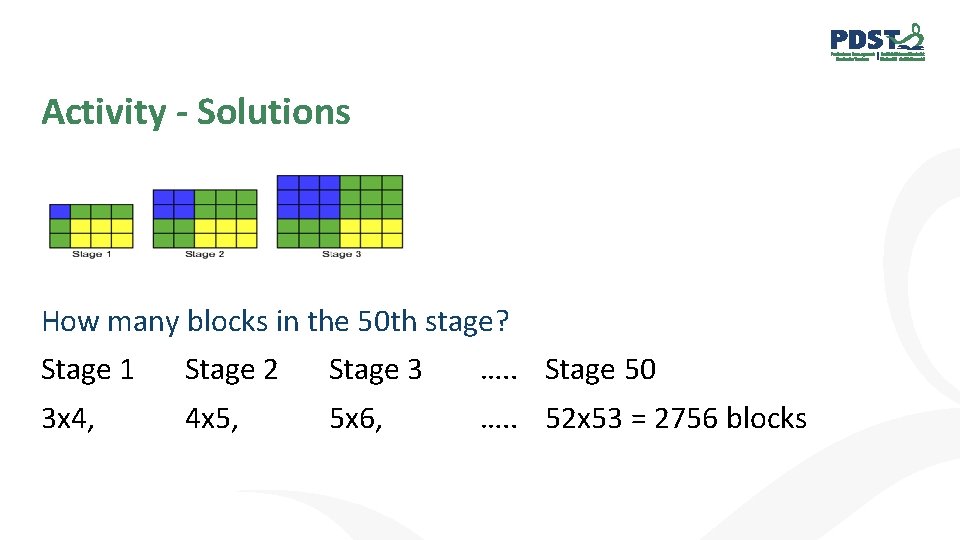
Activity - Solutions How many blocks in the 50 th stage? Stage 1 Stage 2 Stage 3 …. . Stage 50 3 x 4, 4 x 5, 5 x 6, …. . 52 x 53 = 2756 blocks
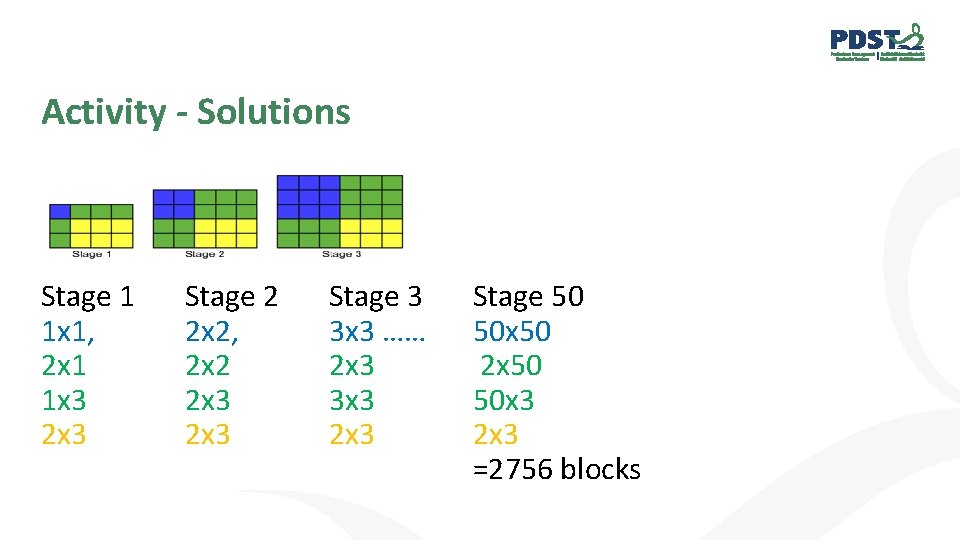
Activity - Solutions Stage 1 1 x 1, 2 x 1 1 x 3 2 x 3 Stage 2 2 x 2, 2 x 2 2 x 3 Stage 3 3 x 3 …… 2 x 3 3 x 3 2 x 3 Stage 50 50 x 50 2 x 50 50 x 3 2 x 3 =2756 blocks
Multiple Representations https: //www. geogebra. org/classic/zfxp 4 kdg
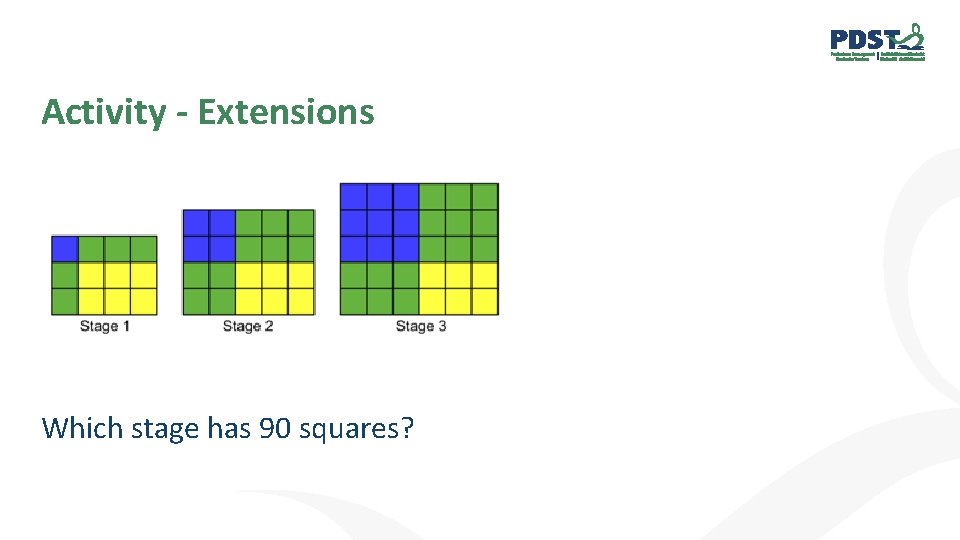
Activity - Extensions Which stage has 90 squares?
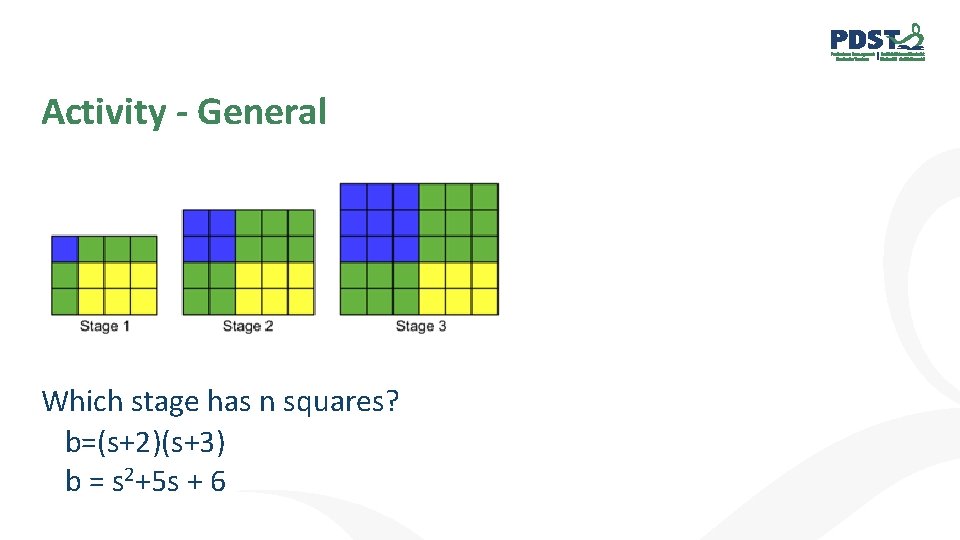
Activity - General Which stage has n squares? b=(s+2)(s+3) b = s 2+5 s + 6

Future Learning Solving Quadratic Equations ● ● ● Key Features of Quadratic Functions Graphical Solutions to Algebraic Inequalities Analysing the Table of Values of Quadratic Functions in Greater Depth

Quadratic Patterns

Summary 1. 2. 3. 4. Students are introduced to new algebraic procedure through the exploration of patterns. Students see the need for new strategies. Students make sense of their learning. Students maintain a positive disposition to their mathematics.

Transformations of Quadratic Patterns
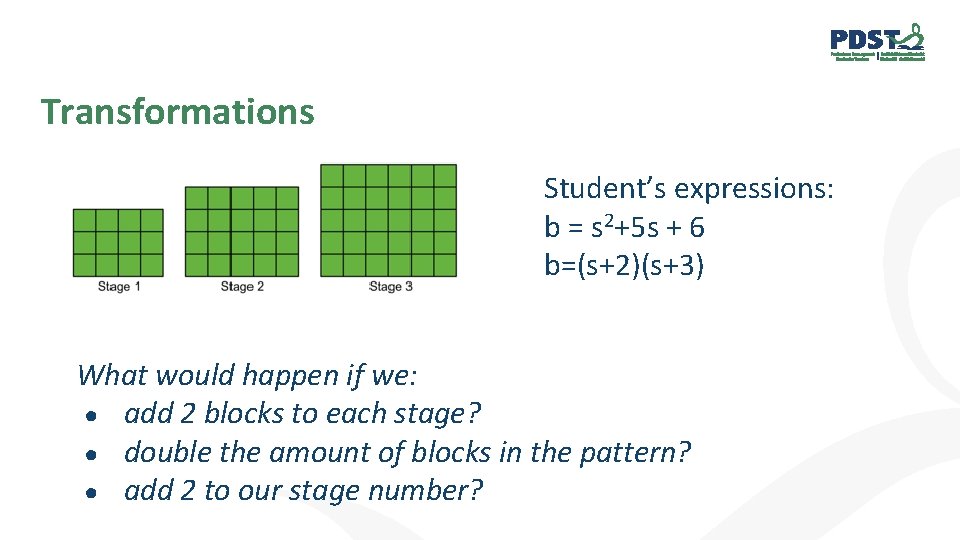
Transformations Student’s expressions: b = s 2+5 s + 6 b=(s+2)(s+3) What would happen if we: ● add 2 blocks to each stage? ● double the amount of blocks in the pattern? ● add 2 to our stage number?
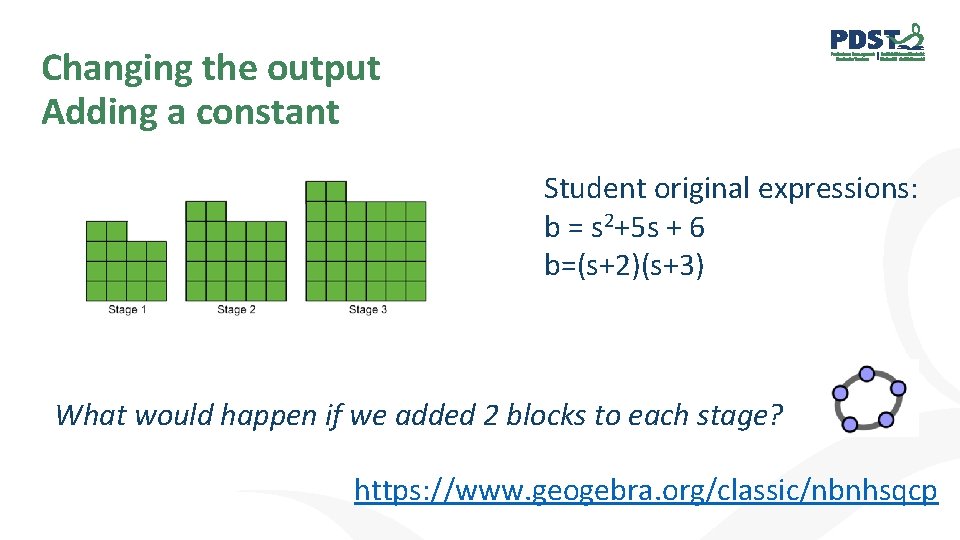
Changing the output Adding a constant Student original expressions: b = s 2+5 s + 6 b=(s+2)(s+3) What would happen if we added 2 blocks to each stage? https: //www. geogebra. org/classic/nbnhsqcp
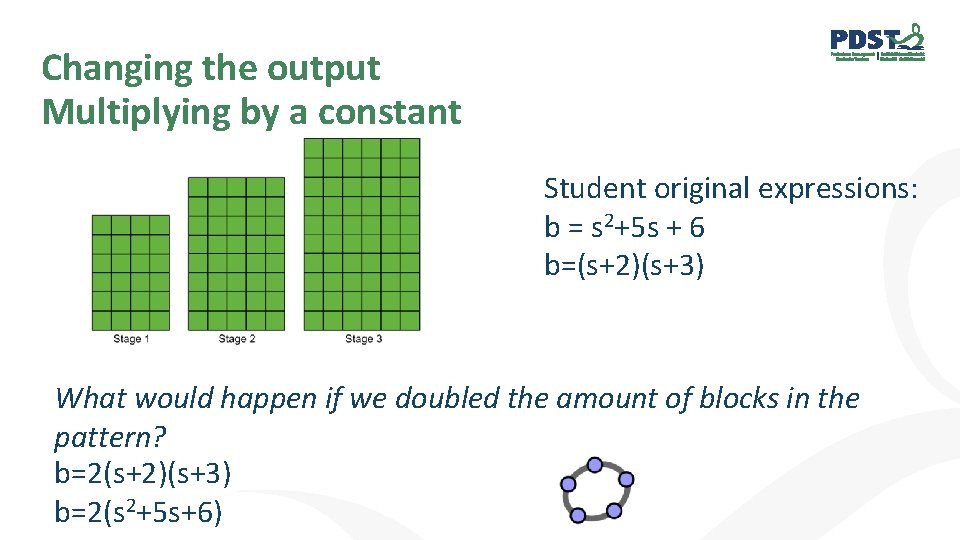
Changing the output Multiplying by a constant Student original expressions: b = s 2+5 s + 6 b=(s+2)(s+3) What would happen if we doubled the amount of blocks in the pattern? b=2(s+2)(s+3) b=2(s 2+5 s+6)
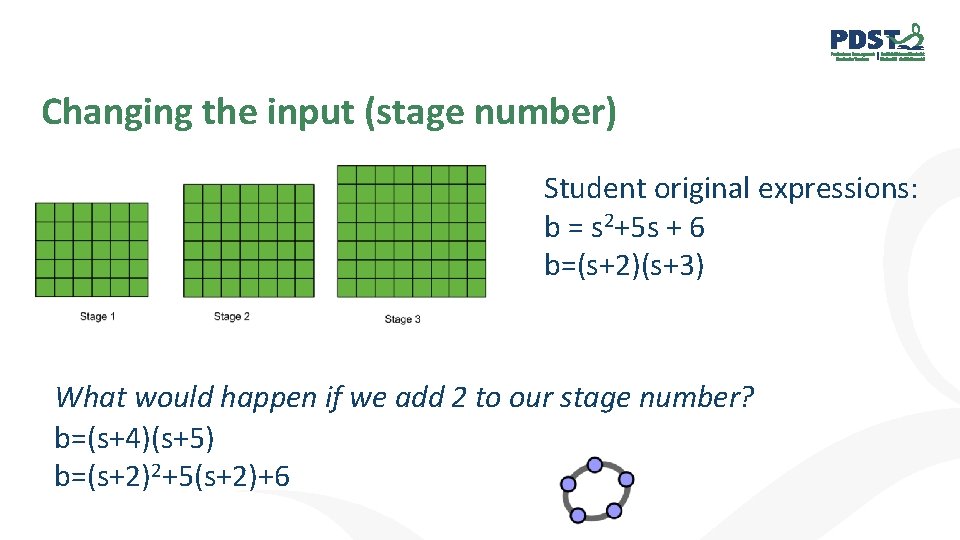
Changing the input (stage number) Student original expressions: b = s 2+5 s + 6 b=(s+2)(s+3) What would happen if we add 2 to our stage number? b=(s+4)(s+5) b=(s+2)2+5(s+2)+6
Transformation of continuous functions https: //www. geogebra. org/m/zj 5 ryy. Up https: //www. geogebra. org/classic/a 6 cddta 6
- Slides: 21