Algebra Skills Year 10 Note 1 Expressions An

Algebra Skills Year 10

Note 1: Expressions An algebraic expression is a statement using symbols. Expressions need to be written as simply as possible. There are rules that should be followed: �A multiplication sign is not used eg. r x s = rs � The number part is written first in an expression eg. y x 5 = 5 y � Letters are written in alphabetical order when multiplying eg. 5 a x g x d = 5 adg � Divisions are written as fractions eg. 3 p ÷ s =

Note 1: Expressions Algebra is used to express rules using symbols. A letter is used to stand for a number. The letter is placed into a formula to explain what happens. e. g. Write the following as a mathematical expression: The sum of all the angles in a polygon is calculated by subtracting two from the number of sides and multiplying this number by 180° S = (n – 2) × 180° BETA: Ex 7. 01 pg 208 Ex 7. 02 pg 209 - 212

Starter: simplify the following expressions


Note 2: Substitution � Substitution means replacing a symbol with a value. Remember to follow the rules of BEDMAS. e. g. Calculate the value of these expressions: 7 x – 1 when x = 2 =7 2– 1 = 14 – 1 = 13 = when f = 2 and g = 6 =4

Note 2: Substitution 5 x 2 - 3 x + 2 when x = -3 = 5 x(-3)2 - 3 -3 + 2 = 45 - − 9 + 2 = 56 BETA: Ex 7. 03 pg 215 Ex 7. 04 pg 216 Ex 7. 05 pg 218

Note 3: Simplifying Multiplication When multiplying terms all numbers and variables can be combined. e. g. Simplify: 3 a x 4 b =12 ab -5 c x 6 d x -2 e = 60 cde BETA: Ex 8. 01. pg 231 Homework book: Ex C pg 75

Note 4: Adding and Subtracting Like Terms � Like terms can be added or subtracted, if they are the same term and of the same power � The sign (+ or -) belongs to the number or variable after it. e. g. Simplify 3 a + a – 2 a = 2 a 4 b – 7 b + 2 b = -b 7 c + 5 d – 9 c + 2 d = -2 c + 7 d 5 ef + 6 fg – 8 fe + 7 hg = -3 ef + 6 fg + 7 gh

Note 4: Adding and Subtracting Like Terms � When we add and subtract like terms with powers, we do not change the powers. e. g. Simplify: k 3 – k 2 + 3 k + 4 k 3 – 6 k 2 = 5 k 3 – 7 k 2 + 3 k BETA: Ex 8. 02 pg 232 Ex 8. 03 pg 233 Homework book: Ex B pg 73

Note 5: Powers y xn means use ‘x’ as a factor n times. exponent, power e. g. p x p = p³ Multiplication When multiplying numbers with the same base, add the powers. e. g. 22 x 23 = (2 x 2) x (2 x 2) = 25 (22+3) y 3 x y 4 = y 7 BETA: 3 q x 7 q = 21 q 2 Ex 8. 05 pg 242 6 r 3 x 5 r 2 s = 30 r 5 s Ex 8. 06 pg 245 Ex 8. 07 pg 246 base

Note 6: Square Roots When simplifying the square root of an algebraic expression � take the square root of the number � divide the power of each variable by 2. Examples: Simplify: = = =6 = x 3 = x 4 2 y 10 2 = 8 x 2 y 5 = x 14 2 y 8 2 = 8 x 7 y 4 BETA: Ex 8. 08 pg 248
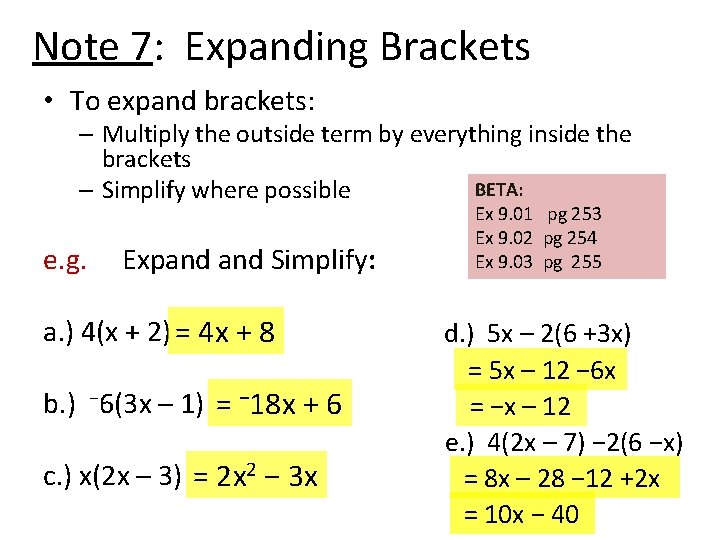
Note 7: Expanding Brackets • To expand brackets: – Multiply the outside term by everything inside the brackets BETA: – Simplify where possible e. g. Expand Simplify: a. ) 4(x + 2) = 4 x + 8 b. ) − 6(3 x – 1) = − 18 x + 6 c. ) x(2 x – 3) = 2 x 2 − 3 x Ex 9. 01 pg 253 Ex 9. 02 pg 254 Ex 9. 03 pg 255 d. ) 5 x – 2(6 +3 x) = 5 x – 12 − 6 x = −x – 12 e. ) 4(2 x – 7) − 2(6 −x) = 8 x – 28 − 12 +2 x = 10 x − 40

Note 8: Factorising BETA: Pg 257 onwards Ex 9. 04, 9. 05, 9. 06, 9. 07 • Factorising is the opposite of expanding – putting brackets back into the algebraic expression: • Look for the highest common factor in the numbers and place it outside the brackets. • Look for any variables (letters) that are common. Take the lowest power and place it outside the brackets. e. g. Factorise: a. ) 4 a + 4 b = 4(a+b) b. ) 3 p – 3 q + 3 r = 3(p – q +r) c. ) 4 x + 8 y + 12 x = 4(x + 2 y + 3 z) d. ) 6 x + 21 = 3(2 x +7) e. ) 24 x - 32 = 8(3 x – 4)
- Slides: 14