Algebra Simplifying Expressions Learning Objective To simplify expressions

Algebra Simplifying Expressions

Learning Objective • To simplify expressions by collecting like terms. Success Criteria • To identify like terms in simple expressions. • To simplify expressions containing more than one variable. • To present a solution in its simplest terms.

Why Do I Need Algebra? Algebra has many uses. It is applied in the development of computer software and video games, as well as in the construction of buildings.

Starting to Use Algebra We want to find out the total cost of these shoes. Each pair is the same price. We could use the letter f to represent the cost of 1 pair. How many pairs have we got? We have 3 pairs, so the total cost is 3 f. f + f = 3 f

The Rules Henry buys 4 apples. He then buys another 3 apples. How much do they cost altogether? Letters are used to represent variables; for this problem, we are going to let the letter a stand for the cost of an apple. The cost of 4 apples (a + a + a) is 4 a, and 3 apples (a + a) is 3 a. Since Henry buys only apples, we only need the variable a. This is called collecting like terms, and allows us to use a simple calculation to find the solution: 4 a + 3 a = 7 a Key Terms variable – a number with an as-yet unknown value. like terms – terms that have the same variables raised to the same power.

Your Turn 1) a+a+a 1) a + a = 3 a 2) b + b = 2 b 3) 2 a + 5 a = 7 a 4) 6 b + b = 7 b 5) 2 b – b = b 6) 3 b – 5 b = -2 b 7) 3 a + 2 a - a 7) 3 a + 2 a – a = 4 a Tip: If we only have 1 of something, we simply write the letter: b instead of 1 b. We can subtract terms as well as add them.

The Rules I want to work out the total cost of a number of apples and bananas. Let’s begin by assigning a variable to each fruit. We’ll use a for the cost of an apple and b for the cost of a bunch of bananas. We now need to count up what we have: 5 apples and 3 bunches of bananas: (a + a + a) + (b + b). Collecting like terms gives us 5 a and 3 b. So the total cost of the apples and bananas is 5 a + 3 b. Remember: we do not know how much each apple or banana costs, so we can only collect the like terms to form an expression for the total cost. Equally, since a and b are different variables, we cannot simply add them together; 5 a + 3 b is the simplest form of the solution rather than 8 ab (this is multiplication rather than addition).

Your Turn 1) x+x+x+y+y+y= 1) 3 x + 3 y 2) 4 p – p – p + 2 p = 2) 2 p 3) 9 x + 2 y + 5 z – 5 x + 3 z - 3 y = 3) 4 x - y + 8 z

Expression Games Cut out the Matching Cards. You should have 16 cards. Each card matches with another card. You should have a pair: one card is its partner expressed in its simplest form. Collect the like terms to find the 8 pairs.

Answers Cut out the cards from your Expression Games Activity Sheet. a+a+a+a 4 a b + 2 a + 3 b - a a + 4 b 2 a + 5 b – 3 a + 6 b 11 b - a 7 a + 5 a - 3 b - b 12 a - 4 b a + 7 b + 5 c – 5 b + 3 a 4 a + 2 b + 5 c -4 a - 2 b - 3 a - 6 b -7 a - 8 b 2 a - 3 b + 5 b + b 2 a + 3 b 5 a + 4 b - 2 b + 3 a - 5 b + 2 a 10 a - 3 b Remember: the function in front of the variable is important. If we are subtracting the variable, we treat it as a negative number.

Memory Pairs Shuffle one set of cards and place them face down on the table. You only need one set of cards between you. With your partner, decide who will go first. Player One selects 2 cards. If they match, they claim that pair of cards. If they do not match, put them back in the same place face down. Player Two now has their turn. Keep going until all the cards are claimed. The winner is the person with the most pairs of cards.

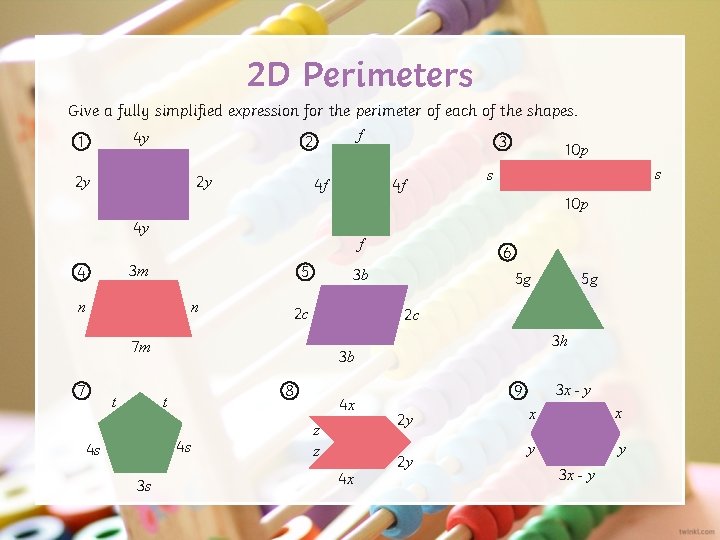
2 D Perimeters Give a fully simplified expression for the perimeter of each of the shapes. f 4 y 1 2 3 10 p 2 y 2 y 4 f 4 f 4 y f 3 m 4 5 n n t 8 4 s 3 s 5 g 3 h 3 b t 4 s 5 g 2 c 7 m 7 10 p 6 3 b 2 c s s 4 x z z 4 x 3 x - y 9 2 y 2 y x x y y 3 x - y

Answers 1) 12 y 2) 10 f 3) 20 p + 2 s 4) 10 m + 2 n 5) 6 b + 4 c 6) 10 g + 3 h 7) 11 s + 2 t 8) 8 x + 4 y + 2 z 9) 8 x