Algebra Notes Algebra contains formulas variables expressions equations

Algebra Notes

Algebra contains formulas, variables, expressions, equations, and inequalities. All of these things help us to solve problems.

• Variables: are letters that represent numbers. – Example: n, x, and y: they are the most commonly used variables. • Algebraic Expression: a combination of numbers, variables, and operations (x, +, -, ). – Example: 2 n + 1 • Verbal Expression: The meaning of an algebraic expression written out in words (directions).

What is the difference between an expression and an equation? An equation has an equal sign and an expression does not.

Examples • A number y increased by seven is twelve § y + 7 = 12 • The product of two and a number is equal to fourteen § 2 n = 14 • Four less a number equals two times that number § 4 – n = 2 n • Twice a number increased by six is ten less than a number § 2 n + 6 = n - 10 • Fourteen divided by a number increased by 6 is seven less than twice a number.

• y+3=9 § a number y increased by three is nine. • 6 n – 17 = 3 n § Six times a number n minus seventeen equals three times that number. • 4 n – 5 = 30/n § The product of four and a number less five is the same as the quotient of thirty and that number • 12 x = 4 + x § Twelve divided by a number equals four more than the number § 12 x - 10 = 8 – n § Ten less than twelve times a number is eight less than that number

Terms of an Expression • Terms are parts of a math expression separated by addition or subtraction signs. 3 x + 5 y – 8 has 3 terms.

Terms of an Expression • Polynomial: an expression that contains one or more terms. Examples: 4 xy x²+ 3 x + 4 3 x + 2 3 Non-Examples: 2 x

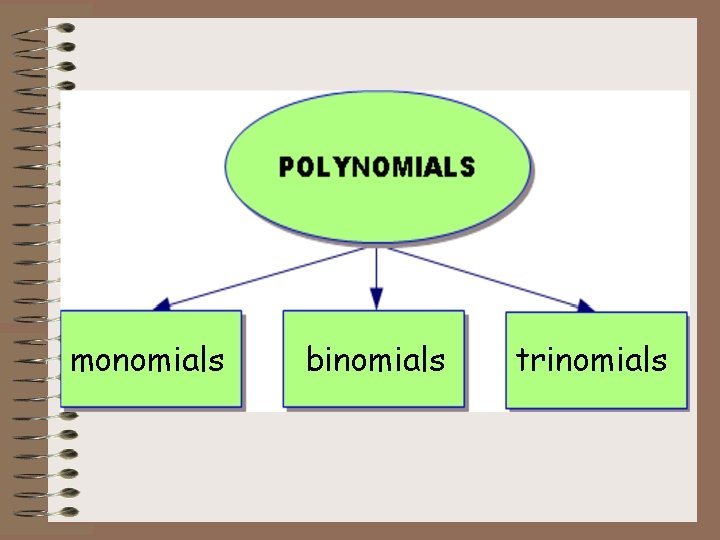
monomials binomials trinomials

Monomials • Monomial: an expression that contains only ONE term. Non-Examples: 4 xy 2 x - 1 3 x² x²+ 3 x - 4

Binomials • Binomial: an expression that contains exactly TWO terms. Examples: Non-Examples: 3 x²+ y - 1 3 x²+ x y²- 7 xy y-5 3 xyz

Trinomials • Trinomial: an expression that contains THREE terms. Examples: Non-Examples:

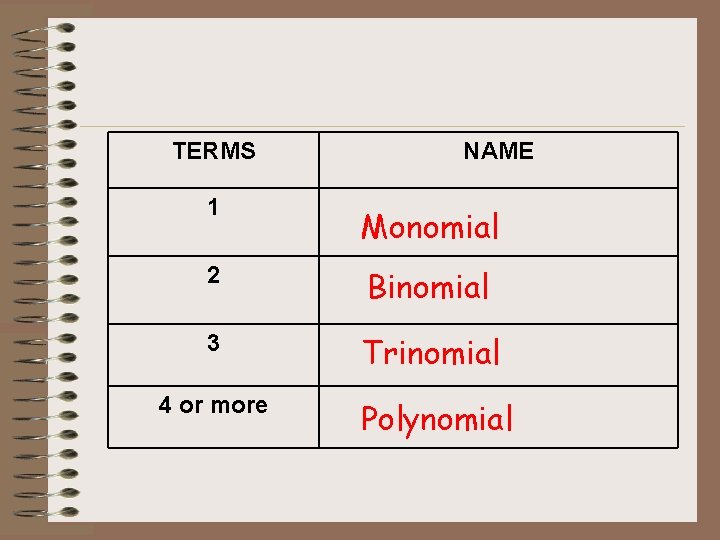
TERMS NAME 1 Monomial 2 Binomial 3 Trinomial 4 or more Polynomial

Like Terms • Like Terms: have the same variables to the same powers 8 x²+2 x²+5 a +a 8 x²and 2 x² are like terms 5 a and a are like terms

LIKE terms: Yes or No? 3 x and 7 x Yes - Like 5 x and 5 y No - Unlike x and x² No - Unlike 6 and 10 Yes - Like

Identify the LIKE terms 3 m – 2 m + 8 – 3 m + 6 5 x + b – 3 x + 4 + 2 x – 1 – 3 b -6 y + 4 yz + 6 x² + 2 yz – 4 y + 2 x² - 5

Coefficients • A Coefficient: a number. The coefficient is written in front of the variable. Example: 6 x The coefficient is 6.

Simplify • Simplify: means to combine like terms. • You can simplify an expression combining like terms. • Combine LIKE terms by adding their coefficients. • You can ONLY combine LIKE TERMS • You can NEVER combine UNLIKE

Simplifying Rules If there is no number written in front of a variable, its coefficient is ONE. Example: x = 1 x When an expression has a subtraction sign in front of it, the subtractions sign stays 3 x with+ 12 that+ term. Example: x – 5 – 2 x 3 x + 1 x – 2 x = 2 x 12 – 5 = 7 = 2 x + 7

Write an expression: + 3 c + 4 c =7 c

Write an expression: 8 a - 1 a = 7 a

Write an expression: + 5 c + 4 d

Write an expression: 5 a – 4 b This expression cannot be simplified. Why not?

Simplify the following: 3 x + 8 x + 2 y = 11 x + 2 y 7 x + 3 y – 4 + 5 x + 2 x = 14 x + 3 y -4 10 x – 3 y + 4 x + 5 y = 14 x + 2 y 5 z – 7 y + 3 x + z – y + x = 6 z – 8 y + 4 x

Simplify the following: 4 x + 5 y + 3 x - 2 y = 7 x + 3 y 5 x + 3 – 4 x - 12 + 4 y = x + 4 y - 9 -3 x + 3 y + 5 y – y = 7 y – 3 x + 3 3+ 4 y + 2 x²- 7 x + 3 xy – 2 xy + 4= 2 x²+ xy -7 x + 4 y + 7

The Distributive Property • Distributive Property: the process of distributing the number on the outside of the parentheses to each term in the inside. a(b + c) = ab + ac Example: 5(x + 7) = 5 • x + 5 • 7 5 x + 35

Practice #1 3(m - 4) 3 • m-3 • 4 3 m – 12 Practice #2 -2(y + 3) -2 • y + (-2) • 3 -2 y + (-6) -2 y - 6

Simplify the following: 3(x + 6) = 3 x + 18 4(4 – y) = 16 – 4 y 6(3 y - 30) = 18 y + 180 5(2 a + 3) = 10 a + 15

Simplify the following: 6(3 y – 5) = 18 y - 30 3 + 4(x + 6) = 4 x + 27 2 x + 3(5 x - 3) + 5 = 17 x - 4

REVIEW

Which of the following is the simplified form of 5 x - 4 - 7 x + 14 ? 1. 2. 3. 4. -12 x + 10 -2 x + 10 2 x - 18 12 x – 18 Answer Now

Bonus! Which of the following is the simplified form of a - 3 a - 4(9 - a) ? 1. 2. 3. 4. -36 3 a - 36 2 a - 36 8 a + 36 Answer Now

Which of the following is the simplified form of (x + 3) – (x + 4) ? 1. 2. 3. 4. -2 x + 7 2 x - 1 7 -1 Answer Now

Which of the following is the simplified form of -4 x + 7 x ? 1. 2. 3. 4. -4 3 x -3 x 4 Answer Now

Which statement demonstrates the distributive property incorrectly? 1. 2. 3. 4. 3(x + y + z) = 3 x + 3 y + 3 z (a + b) c = ac + bc 5(2 + 3 x) = 10 + 3 x 6(3 k - 4) = 18 k - 24 Answer Now

Steps to Solving Equations Equation: a mathematical sentence using an equal (=) sign. • Step 1: Get rid of the 10. Look at the sign in front of the 10, since it is subtraction we need to use the opposite operation (addition) to cancel out the 10 – Add 10 to both sides. Remember, what you do – 10 = you 50 have to do to to one side of the 2 n equation, +1 +1 the other. 0 0 2 n = 60

Steps to Solving Equations • Step 2: Next, we need to look at what else is happening to the variable. 2 n means that two is being multiplied to n, therefore we need to do the opposite (division) to “undo” the multiplication. – Divide both sides by 2. Remember, what you do to one side of the equation, you have to do to the other 2 n. = 60 2 2 n = 30

Steps to Solving Equations • Step 3: “Plug & Chug” then CHECK your solution!! First, rewrite the original equation – We already solved for n, so wherever you see the variable, n, plug in the answer. – Evaluate the equation, SHOWING ALL WORK! – Does it check? 2 n – 10 = 50 2 (30) – 10 = 60 – 50 10 = 50 50 = 50

Solve & Check n = 23 1. 5 n – 15 = 100 2. 105 = 10 n + 5 n = 10 3. n/5 + 3 = 6 n = 15 n = 42 4. -44 + 7 n = 250 5. 200 = 100 – 25 nn = -4 6. 12 + 4 n = 112 n = 25

Steps to Solving Multi-Step Equations • Step 1: Distribute if necessary variable. – Distribute the 4 to the n and 5. 4(n – 5) - 7 = 9 + 2 n – 4 n 4 n – 20 - 7 = 9 + 2 n – 4 n

Steps to Solving Multi. Step Equations • Step 2: Combine like terms on each side of the equations. – On the left side -20 and -7 combine to get -27 – On the right side 2 n and -4 n combine to get -2 n 4 n – 20 - 7 = 9 + 2 n – 4 n 4 n – 27 = 9 – 2 n

Steps to Solving Multi. Step Equations • Step 3: Get all variables to one side of the equation. – First we want to get rid of the -27. Look at the sign in front of -27, since it is subtraction (or a negative) we need to use the opposite operation (addition) to cancel it out. Therefore add 27 to both 4 nsides – 27. = 9 – +22 n+2 7 7 4 n = 36 – 2 n

Steps to Solving Equations • Step 4: Get all “plain numbers” to one side of the equation – First we want to get rid of the -2 n. Look at the sign in front of -2 n, since it is subtraction (or a negative) we need to use the opposite operation (addition) to cancel it out. Therefore add 2 n to both 4 n sides. – 2 n = 36 +2 n 6 n = 36

Steps to Solving Multi. Step Equations • Step 5: Next, since we have all the variables on one side and all the “plain numbers” on the other side we need to look at what else is happening to the variable. – 6 n means the 6 is being multiplied by n, therefore we need to do the opposite (division) 6 n = 36 So, divide both to “undo” the multiplication. 6 6 sides by 6. n= 6

Steps to Solving Multi. Step Equations • Step 6: “Plug & Chug” then CHECK your solution!! First, rewrite the original equation – We already solved for n, so wherever you see the variable, n, plug in the answer. – Evaluate the equation, SHOWING ALL WORK! 4(n – 5) - 7 = 9 + 2 n – – Does it check? 4(6 – 5) - 4 n 7 = 9 + 2(6) – 4(1) - 7 =4(6) 9 + 12 – 24 4 – 7 = 21 -3 =24 -3

Solve & Check r = -2 1. 9 + 5 r = -17 – 8 r 2. 3(n + 5) + 2 = 26 n = 3 y = -11 3. 58 + 3 y = -4 y – 19 v = 12 4. 4 – 2(v – 6) = -8 5. 5(y – 2) + 6 = 6 y + 2 y – 14 y–=y 5

LESCA An electrician charges $50 to come to your house. Then he charges $25 for each hour he spends there. If the electrician charges you a total of $125, how many hours did he spend there? Let Statement: Let number of hours = x Equation: $50 + $25 x = $125 Solution: 25 x = 75 x=3 Check: 50 + 25(3) = 125 50 + 75 = 125 Answer Sentence: The electrician was there for 3

LESCA The sum of two consecutive integers is 73. What are the numbers? Let Statement: Let first number = x = 36 second number = x + 1 = 37 Equation: x + 1 = 73 2 x = 72 Solution: x = 36 Check: 36 + 1 = 73 73 = 73 Answer Sentence: The numbers are 36 and 37.

LESCA A taxi charges $1. 50 plus a fee of $0. 60 for each mile traveled. If a ride costs $5. 40, how many miles was the ride? =6 Let Statement: Let number of miles = x Equation: $1. 50 + $0. 60 x = $5. 40. 6 x = 3. 6 Solution: x=6 Check: 1. 50 + 0. 60(6) = 5. 40 1. 5 + 3. 6 = 5. 40 5. 4 = 5. 4 Answer Sentence: The ride was 6 miles.

LESCA Two years of internet service costs $685, including the installation fee of $85. What is the monthly fee? = 25 Let Statement: Let monthly fee = x Equation: 24 x + $85 = $685 24 x = 600 Solution: x = 25 Check: 24(25) + 85 = 685 600 + 85 = 685 Answer Sentence: The monthly fee is $25.

LESCA The sum of two numbers is 99. The difference of the two numbers is 9. What are the numbers? = 54 Let Statement: Let first number = x = 45 second number = x – 9 Equation: x + x - 9 = 99 2 x = 108 Solution: x = 54 Check: 36 + 1 = 73 73 = 73 Answer Sentence: The numbers are 45 and

Inequalities • Inequality: a mathematical sentence using <, >, ≥ , or ≤. – Example: 3 + y > 8. • Inequalities use symbols like < and > which means less than or greater than. • They also use the symbols ≤ and ≥ which means less than or equal to and greater than or equal to.

What’s the difference? • x < 4 means that x is less than 4 – 4 is not part of the solution – What number is in this solution set? • x ≤ 4 means that x can be less than OR equal to 4 – 4 IS part of the answer – What number is in this solution set?

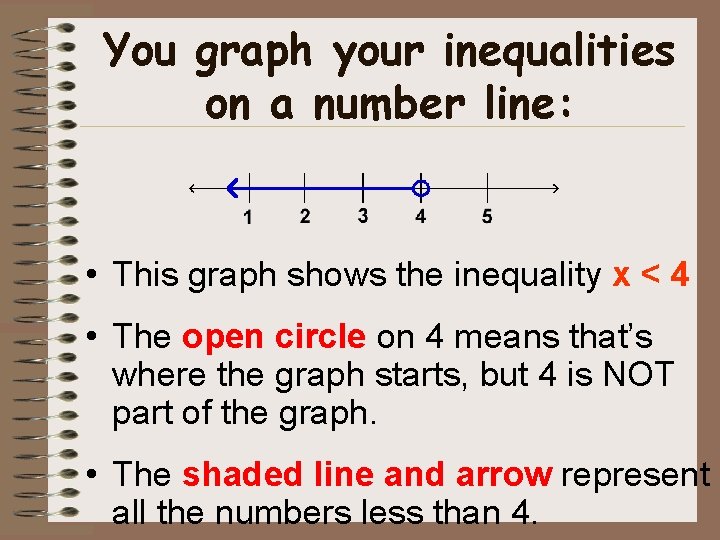
You graph your inequalities on a number line: • This graph shows the inequality x < 4 • The open circle on 4 means that’s where the graph starts, but 4 is NOT part of the graph. • The shaded line and arrow represent all the numbers less than 4.

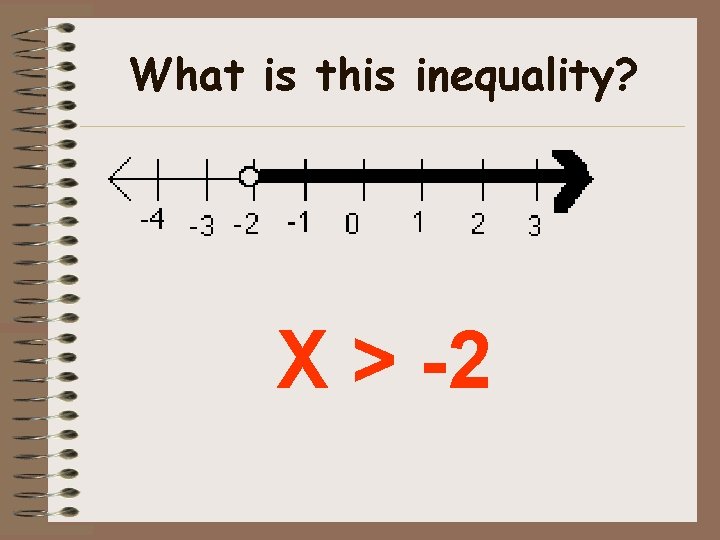
What is this inequality? X > -2

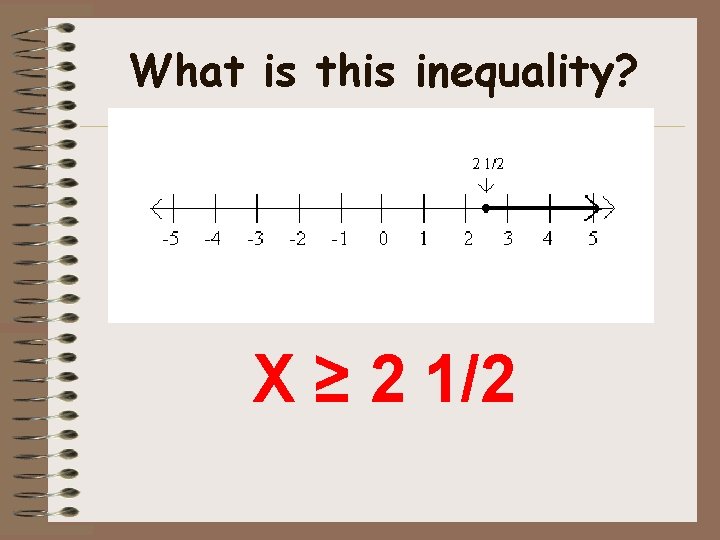
What is this inequality? X ≥ 2 1/2

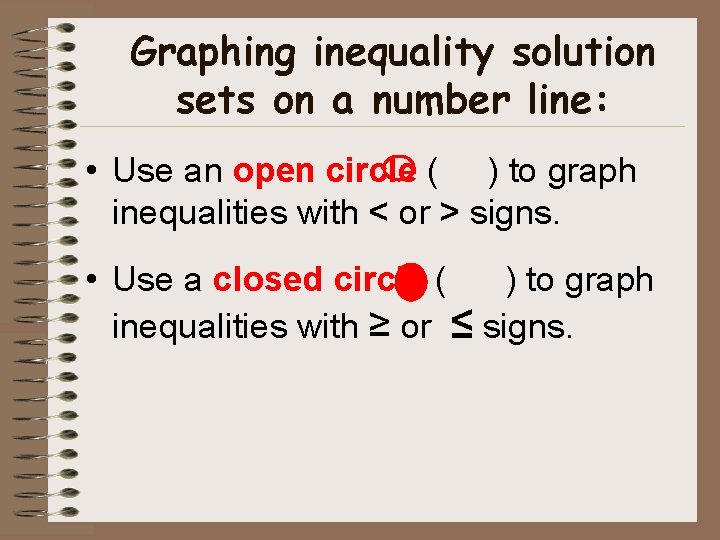
Graphing inequality solution sets on a number line: • Use an open circle ( ) to graph inequalities with < or > signs. • Use a closed circle ( ) to graph inequalities with ≥ or ≤ signs.

What do you think this symbol means? ≠ Does not equal… Example: x ≠ 7

Graph x ≠ -1 • X ≠ -1 would include everything on the number line EXCEPT -1. • Use an open circle to show that -1 is NOT a part of the graph.

Solve, Graph, & Check 1. 2 n + 7 > 13 n 2. 3 y – 9 ≤ -3 >3 y ≤ 2 3. 2 n + 10 ≥ 6 n ≥ -2 4. 5 n + 4 < 4 nn < -4 5. 3 x – 3 ≤ 9 x≤ 4 6. 4 + 7 x < 25 x < 3

Evaluating Formulas • Evaluate: means to replace variables with their numerical values and then solve – Example: n + 3 = 5; n = 2 – Example: y – 3, if y = 9 Then, y – 3 = 9 – 3 = 6