Algebra II Linear Relations Solutions Revision Section B

Algebra II – Linear Relations Solutions: Revision – Section B More challenging problems CHAPTER 03

Revision and Exam Style Questions: Section B 03 1. 2(x + 10) = 12 – 3(x – 6) (expand) 2 x + 20 = 12 – 3 x + 18 (collect like terms) 2 x + 20 = 30 – 3 x (Add 3 x to both sides) 5 x + 20 = 30 (Subtract 20 from both sides) 5 x = 10 (Divide both sides by 5)

Revision and Exam Style Questions: Section B 03 1. Verify this solution: 2(x + 10) = 12 – 3(x – 6) 2(2 + 10) = 12 – 3(2 – 6) 2(12) = 12 – 3(– 4) 24 = 12 + 12 24 = 24

03 2. Revision and Exam Style Questions: Section B Find the value of x, which satisfies the equation and verify your solution.

03 2. Revision and Exam Style Questions: Section B Find the value of x, which satisfies the equation and verify your solution. Verify this solution:

03 3. (i) Revision and Exam Style Questions: Section B The temperature, C, in degrees Celsius, of a liquid in an insulated container is related to time, t, in hours by the following function: C = 78 − 8 t Find the temperature of the liquid in the container after 2∙ 5 hours. C = 78 – 8 t C(2· 5) = 78 – 8(2 5) = 78 – 20 C(2· 5) = 58°C

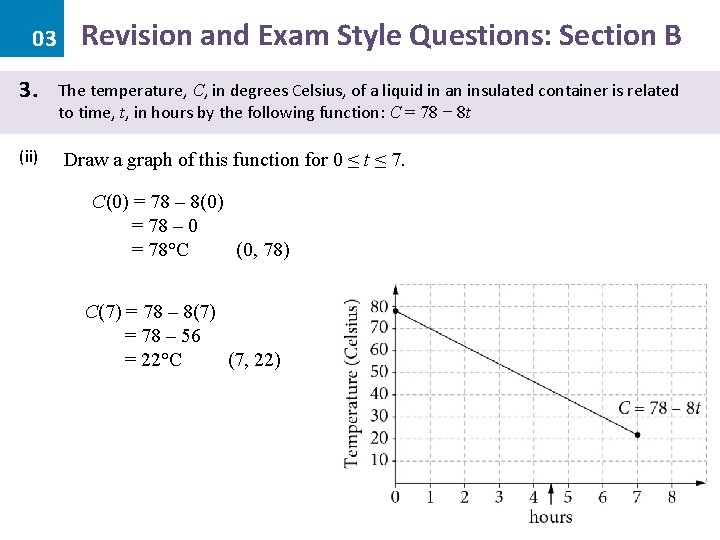
03 3. (ii) Revision and Exam Style Questions: Section B The temperature, C, in degrees Celsius, of a liquid in an insulated container is related to time, t, in hours by the following function: C = 78 − 8 t Draw a graph of this function for 0 ≤ t ≤ 7. C(0) = 78 – 8(0) = 78 – 0 = 78°C (0, 78) C(7) = 78 – 8(7) = 78 – 56 = 22°C (7, 22)

03 Revision and Exam Style Questions: Section B 3. The temperature, C, in degrees Celsius, of a liquid in an insulated container is related to time, t, in hours by the following function: C = 78 − 8 t (iii) Use this graph to estimate how long it will take for the liquid to reach 42°C. • Go to 42 on the y-axis • Draw a dotted line across until you touch the graph. • Draw a dotted line from this point, down to the x-axis. • Read the value off the x-axis. C = 42°C when t = 4· 5 hours. Acceptable answers would be 4· 5 ± 0· 1

03 3. (iv) Revision and Exam Style Questions: Section B The temperature, C, in degrees Celsius, of a liquid in an insulated container is related to time, t, in hours by the following function: C = 78 − 8 t Use your graph to estimate the time it takes for the temperature to drop from 65°C to 25°C. • Go to 25 on the y-axis. • Draw a dotted line across until you touch the graph. • Draw a dotted line from this point, down to the x-axis. • Read the value off the x-axis. • Repeat for 65 on the y-axis.

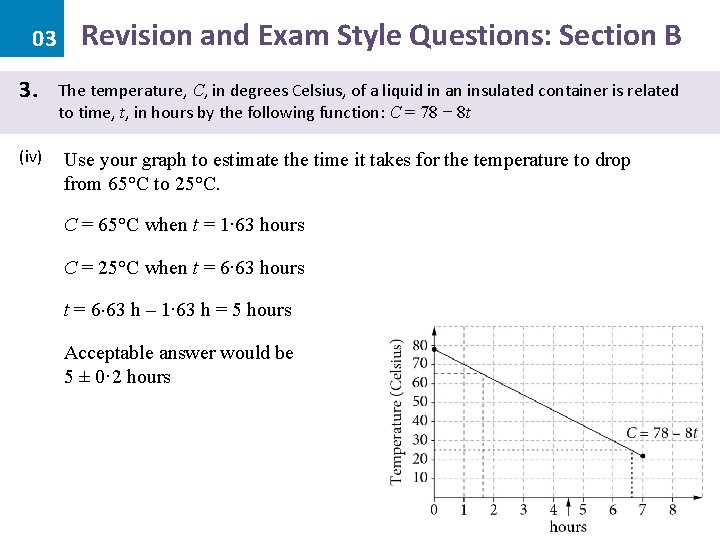
03 3. (iv) Revision and Exam Style Questions: Section B The temperature, C, in degrees Celsius, of a liquid in an insulated container is related to time, t, in hours by the following function: C = 78 − 8 t Use your graph to estimate the time it takes for the temperature to drop from 65°C to 25°C. C = 65°C when t = 1∙ 63 hours C = 25°C when t = 6∙ 63 hours t = 6 63 h – 1∙ 63 h = 5 hours Acceptable answer would be 5 ± 0· 2 hours

03 4. Revision and Exam Style Questions: Section B Solve the following pair of simultaneous equations:

03 4. Revision and Exam Style Questions: Section B Solve the following pair of simultaneous equations: Solving:

03 4. Revision and Exam Style Questions: Section B Solve the following pair of simultaneous equations: Let x = – 2: 3 x – 5 y = – 21 3(– 2) – 5 y = – 21 – 6 – 5 y = – 21 – 5 y = – 15 y=3 (Add 6 to both sides) (Divide both sides by − 5)

03 5. Revision and Exam Style Questions: Section B Solve the equation and verify your answer.

03 5. Revision and Exam Style Questions: Section B Solve the equation and verify your answer. Verify:

03 6. (i) Revision and Exam Style Questions: Section B Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. Write a function to represent Kathy’s weight after W weeks. Initial value = 115 Rate of change = – 1∙ 5 per week m = 115 – 1∙ 5 W m is Kathy’s weight, W is the number of weeks.

03 6. (ii) Revision and Exam Style Questions: Section B Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. What is the rate of change (slope) of this function? Rate of change = – 1∙ 5

03 6. (iii) Revision and Exam Style Questions: Section B Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. Draw a graph of this function, to represent weight for the first 30 weeks. m(0) = 115 – 1∙ 5(0) = 115 – 0 = 115 kg (0, 115) m(30) = 115 – 1∙ 5(30) = 115 – 45 = 70 kg (30, 70)

03 6. (iv) Revision and Exam Style Questions: Section B Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. The point (5, 107∙ 5) is on the graph. Write a sentence that describes the meaning of this ordered pair. After 5 weeks at the weight-loss club, Kathy’s weight is 107∙ 5 kg

Revision and Exam Style Questions: Section B 03 6. (v) Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. Use your graph to find Kathy’s weight after eight weeks. • Go to 8 on the x-axis • Draw a line up until you touch the graph After 8 weeks the weight is 103 kg Acceptable answers would be 103 ± 2 kg

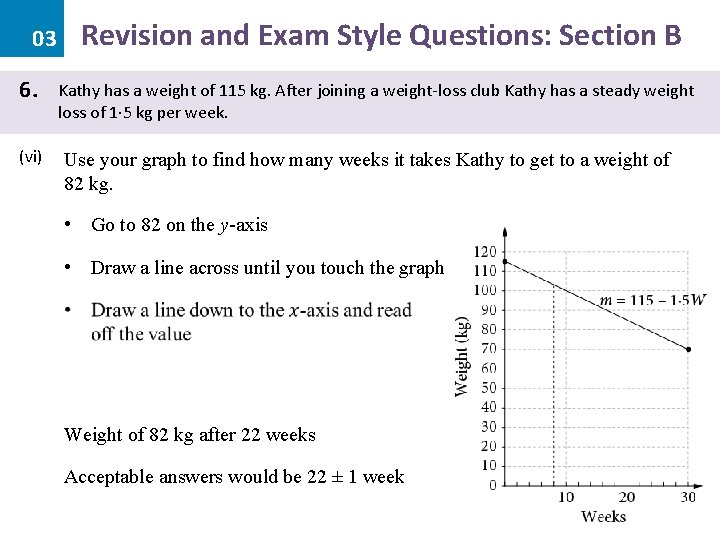
Revision and Exam Style Questions: Section B 03 6. (vi) Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. Use your graph to find how many weeks it takes Kathy to get to a weight of 82 kg. • Go to 82 on the y-axis • Draw a line across until you touch the graph Weight of 82 kg after 22 weeks Acceptable answers would be 22 ± 1 week

03 6. Revision and Exam Style Questions: Section B Kathy has a weight of 115 kg. After joining a weight-loss club Kathy has a steady weight loss of 1· 5 kg per week. (vii) Do you think this graph is a good representation of a person’s weight loss? Give a reason for your answer. No, it is not possible to sustain a constant weight loss over a prolonged period of time. If the weight loss stayed at this rate, Kathy would eventually end up with a weight of 0 kg, which is not possible.

03 7. Revision and Exam Style Questions: Section B Solve the following inequality and graph the solution set on a number line:

03 7. Revision and Exam Style Questions: Section B Solve the following inequality and graph the solution set on a number line: ℝ So x – 1· 1, x ℝ

03 8. Revision and Exam Style Questions: Section B Solve the equations below to find the values of p and q. 3 p − 4 q = 6 and p = 3 q + 2 3 p – 4 q = 6 (Subtract 3 q to both sides) p – 3 q = 2 Solve: 3 p – 4 q = 6 p – 3 q = 2 (Multiply both sides by – 3) 3 p – 4 q = 6 – 3 p + 9 q = – 6 5 q = 0 q=0 (Add rows) (Divide both sides by 5)

03 8. Revision and Exam Style Questions: Section B Solve the equations below to find the values of p and q. Let q = 0: 3 p – 4 q = 6 3 p – 4(0) = 6 3 p = 6 p=2 (Divide both sides by 3)

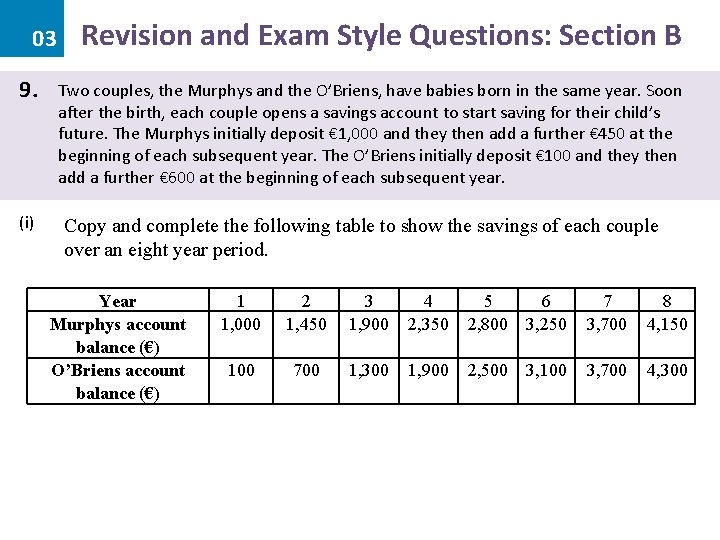
03 9. (i) Revision and Exam Style Questions: Section B Two couples, the Murphys and the O’Briens, have babies born in the same year. Soon after the birth, each couple opens a savings account to start saving for their child’s future. The Murphys initially deposit € 1, 000 and they then add a further € 450 at the beginning of each subsequent year. The O’Briens initially deposit € 100 and they then add a further € 600 at the beginning of each subsequent year. Copy and complete the following table to show the savings of each couple over an eight year period. Year Murphys account balance (€) O’Briens account balance (€) 1 1, 000 2 1, 450 3 1, 900 4 2, 350 5 6 2, 800 3, 250 7 3, 700 8 4, 150 100 700 1, 300 1, 900 2, 500 3, 100 3, 700 4, 300

03 9. (ii) Revision and Exam Style Questions: Section B Two couples, the Murphys and the O’Briens, have babies born in the same year. Soon after the birth, each couple opens a savings account to start saving for their child’s future. The Murphys initially deposit € 1, 000 and they then add a further € 450 at the beginning of each subsequent year. The O’Briens initially deposit € 100 and they then add a further € 600 at the beginning of each subsequent year. In what year will both couples have the same account balance? Year 7 both account balances are equal.

03 9. (iii) Revision and Exam Style Questions: Section B Two couples, the Murphys and the O’Briens, have babies born in the same year. Soon after the birth, each couple opens a savings account to start saving for their child’s future. The Murphys initially deposit € 1, 000 and they then add a further € 450 at the beginning of each subsequent year. The O’Briens initially deposit € 100 and they then add a further € 600 at the beginning of each subsequent year. Find, in terms of n, formulae that give the balance in each of the bank accounts in the nth year. The families have been adding into the account for one year fewer than the year number. That is, on the sixth year, they have the initial sum plus five additional contributions in the account. Murphy: Tn = 1000 + 450(n – 1) = 550 + 450 n O’Brien: Tn = 100 + 600(n – 1) = – 500 + 600 n

03 9. (iv) Revision and Exam Style Questions: Section B Two couples, the Murphys and the O’Briens, have babies born in the same year. Soon after the birth, each couple opens a savings account to start saving for their child’s future. The Murphys initially deposit € 1, 000 and they then add a further € 450 at the beginning of each subsequent year. The O’Briens initially deposit € 100 and they then add a further € 600 at the beginning of each subsequent year. Use the formulae from part (iii) to verify your answer to part (ii) algebraically. Find where the two balances are equal: Murphy = O’Brien 550 + 450 n = – 500 + 600 n 1050 + 450 n = 600 n 1050 = 150 n 7=n (Add 500 to both sides) (Subtract 450 n to both sides) (Divide both sides by 150) �After 7 years the account balances are equal.

03 9. (v) Revision and Exam Style Questions: Section B Two couples, the Murphys and the O’Briens, have babies born in the same year. Soon after the birth, each couple opens a savings account to start saving for their child’s future. The Murphys initially deposit € 1, 000 and they then add a further € 450 at the beginning of each subsequent year. The O’Briens initially deposit € 100 and they then add a further € 600 at the beginning of each subsequent year. If the couples continue to save at the same rate, how much will be in each account in the 15 th year (i. e. when n = 15)? Murphy: T 15 = 550 + 450(15) = 550 + 6750 = € 7, 300 O’Brien: T 15 = – 500 + 600(15) = – 500 + 9000 = € 8, 500

Revision and Exam Style Questions: Section B 03 10. P: 2 x – 3 5 2 x 8 x 4 (Add 3 to both sides) (Divide both sides by 2) x ℤ

03 10. Revision and Exam Style Questions: Section B (ii) Find Q, the solution set of Z – 2 – 3 x < 7 – 3 x < 9 x > – 3, (Add 2 to both sides) (Divide both sides by – 3 and change the direction of the inequality) x ℤ

03 10. Revision and Exam Style Questions: Section B (iii) List the elements of P Q: – 3 < x 4, x ℤ x = – 2, – 1, 0, 1, 2, 3, 4.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (i) Write a function to represent the cost of using company A. Explain any letters you use in your function. C = 300 + 15 G C is the total cost, G is the number of guests.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (ii) Write a function to represent the cost of using company B. Explain any letters you use in your function. C = 25 G C is the total cost, G is the number of guests.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (iii) Using the same axes and scale, graph each function to show the cost of catering for up to 50 people. Clearly indicate which graph represents which company. B: C = 25 G A: C = 300 + 15 G C(0) = 25(0) C(0) = 300 + 15(0) = 300 (0, 300) C(50) = 300 + 15(50) = 1050 =0 (0, 0) C(50) = 25(50) (50, 1050) = 1250 (50, 1250)

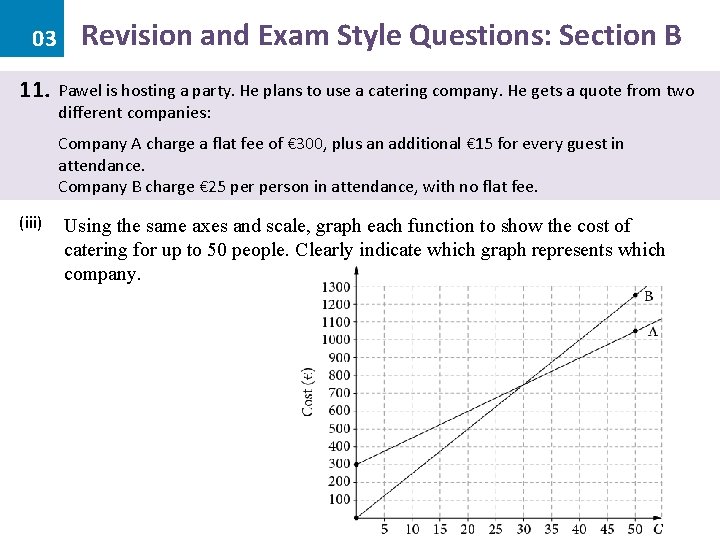
03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (iii) Using the same axes and scale, graph each function to show the cost of catering for up to 50 people. Clearly indicate which graph represents which company.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (iv) If Pawel is inviting 22 people, which company should he use? Justify your answer. 22 Guests: Company A Company B C = 300 + 15(12) C = 25(22) C = 300 + 330 C = € 550 C = € 630 Company B is cheaper for 22 guests.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (v) If Pawel is inviting 45 people, which company should he use? Justify your answer. 45 Guests: Company A Company B C = 300 + 15(45) C = 25(45) C = 300 + 675 C = € 1, 125 C = € 975 Company A is cheaper for 45 guests.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (vi) Using the graphs, or otherwise, find how many guests Pawel could invite so that the cost incurred would be the same from both companies. A=B 300 + 15 G = 25 G 300 = 10 G (Subtract 15 G from both sides) (Divide both sides by 10) 30 = G 30 Guests would incur the same cost for both companies.

03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (vi) Using the graphs, or otherwise, find how many guests Pawel could invite so that the cost incurred would be the same from both companies. A: C = 300 + 15(30) = 300 + 450 = 750 B: C = 25(30) = 750 30 Guests would incur the same cost of € 750 from both companies.

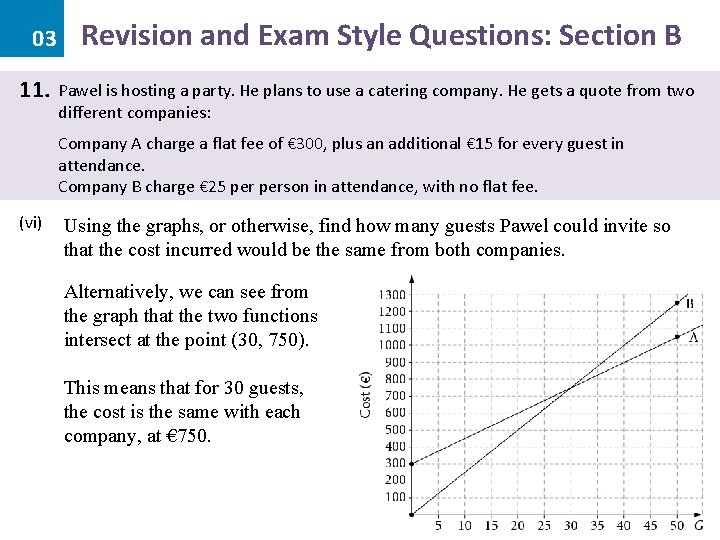
03 11. Revision and Exam Style Questions: Section B Pawel is hosting a party. He plans to use a catering company. He gets a quote from two different companies: Company A charge a flat fee of € 300, plus an additional € 15 for every guest in attendance. Company B charge € 25 person in attendance, with no flat fee. (vi) Using the graphs, or otherwise, find how many guests Pawel could invite so that the cost incurred would be the same from both companies. Alternatively, we can see from the graph that the two functions intersect at the point (30, 750). This means that for 30 guests, the cost is the same with each company, at € 750.