ALGEBRA I SETS UNION and INTERSECTION U A

ALGEBRA I @ SETS : UNION and INTERSECTION

U A 1 2 9 3 SET : a collection of objects. A = {1, 2, 3, 4, 5}. 4 5 6 7 B = {4, 5, 6, 7, 8} 8 10 B VENN DIAGRAM : a picture of a set or a group of sets. ELEMENT or OBJECT : a member of a set. Created by a guy named Venn…. but I don’t know venn he did it.

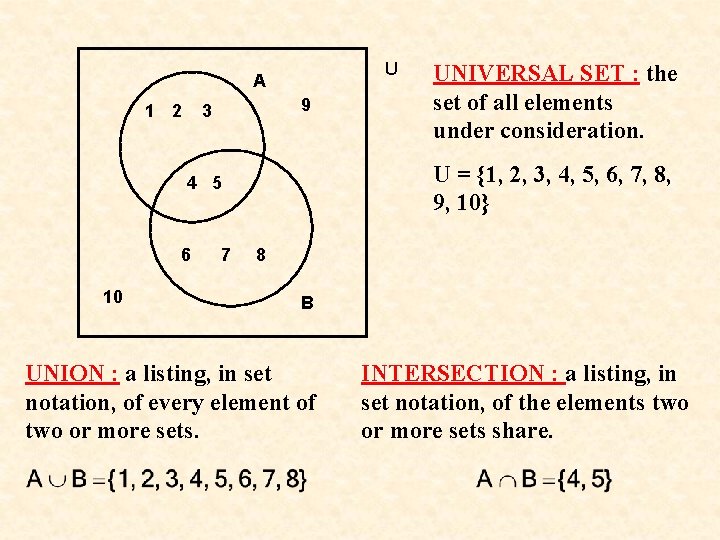
U A 1 2 9 3 U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} 4 5 6 10 7 UNIVERSAL SET : the set of all elements under consideration. 8 B UNION : a listing, in set notation, of every element of two or more sets. INTERSECTION : a listing, in set notation, of the elements two or more sets share.

EMPTY SET : a set that contains no elements, denoted by the symbol Ø. Examples : FINITE SET : a set that contains a definite number of elements. (You can count them!) Examples : INFINITE SET : a set that contains an indefinite number of members. (You can’t count them. ) Examples :

OVERLAPPING SETS : two or more sets that share at least one element. Examples : A B Other examples? U Sets A and B overlap.

ROSTER METHOD : a way to write the elements of a set by listing all of the elements. Examples : RULE METHOD : a way to write the elements of a set by definition. Examples : DISJOINT : two sets are disjoint if they have no elements in common. Examples : U A B

Draw Venn Diagrams for each of the following sets. 1) U = {letters of the English alphabet} A = {different letters in the word ‘baseball’} B = {different letters in the word ‘basket’} 2) U = {a, b, c, d, e, f, g, h, I, j, k, l, m} X = {a, b, c, d, e , f, g} Y = {e, f, g, h, i, j, k}

Find the union ( ) and intersection ( ) of each pair of sets. 3) U = {whole numbers from 1 -20 inclusive} P = {prime numbers less than 20} D = {odd whole numbers less than 20} 4) U = {letters of the English alphabet} F = {different letters in the word ‘foot’} B = {different letters in the word ‘base’} Note : sets F and B are disjoint!