ALGEBRA I SECTION 8 1 ADDING and SUBTRACTING

ALGEBRA I @ SECTION 8 -1 : ADDING and SUBTRACTING POLYNOMIALS

MONOMIAL : a number, a variable, or the product of a number and a variable. Examples : DEGREE of a MONOMIAL : is the sum of the exponents of the variables. 1) Find the degree of the monomial examples we just wrote. BINOMIAL : the sum or difference of two monomials. Examples :

TRINOMIAL : the sum and/or difference of three monomials. Examples : POLYNOMIAL : is a monomial or the sum or difference of monomials. A polynomial can have 1, 2, 3, or more terms. Examples : The degree of a polynomial is the largest degree of a monomial in the polynomial. 2) Find the degree of each polynomial we just wrote.

STANDARD FORM of a POLYNOMIAL : means the monomial’s degrees decrease from left to right. Examples : NAMES OF POLYNOMIAL DEGREE NAME 0 constant 1 linear 2 quadratic 3 cubic 4 quartic EXAMPLE

Write each polynomial in Standard Form. Then, name the polynomial by its degree and number of terms. 3) 4 x + 5 x 2 ANSWER : 5 x 2 + 4 x, quadratic binomial 4) 4 x + 1 – 5 x 2 + 7 x ANSWER : -5 x 2 + 11 x + 1, quadratic trinomial 5) 3 x 2 + 2 x – 1 + 7 x 3 ANSWER : 7 x 3 + 3 x 2 + 2 x – 1, cubic trinomial

In order to add or subtract polynomials, you add/subtract like terms. There are two ways to add or subtract polynomials – horizontally and vertically. We’ll try both methods. 6) (4 x - 3) + (2 x + 5) ANSWER : 6 x + 2 7) (x² + 2 x - 5) + (3 x² - x + 4) ANSWER : 4 x 2 + x - 1

8) 4 x - 3 (+) 2 x + 5 (Align all like terms) ANSWER : 6 x + 2 9) a² - 2 ab + 4 b² (+) 7 a² - 2 b² ANSWER : 8 a 2 – 2 ab + 2 b 2

To subtract polynomials, distribute the negative and add like terms. 10) (6 x + 5) - (3 x + 1) ANSWER : 3 x + 4 11) (3 x - 2) - (-4 x + 2 x² - 9) ANSWER : -2 x 2 + 7 x + 7
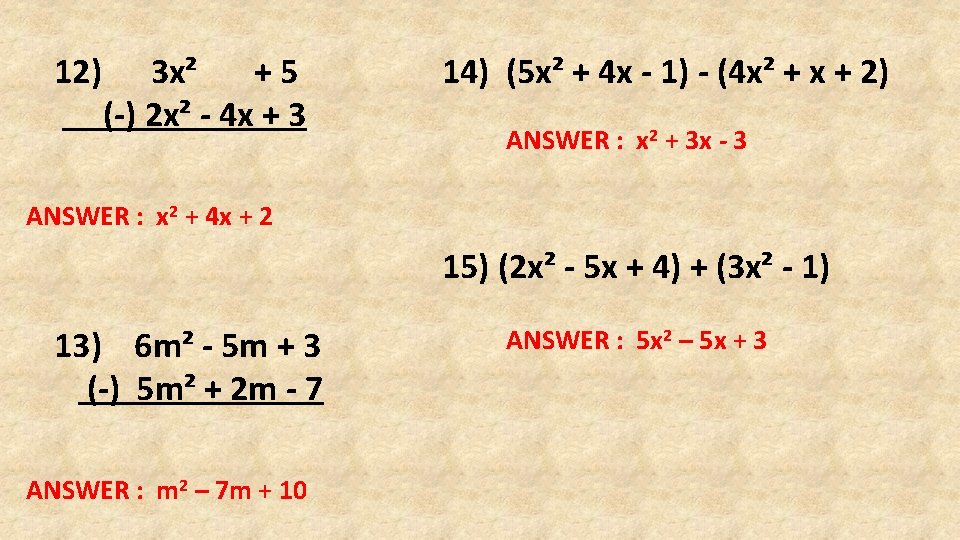
12) 3 x² +5 (-) 2 x² - 4 x + 3 14) (5 x² + 4 x - 1) - (4 x² + x + 2) ANSWER : x 2 + 3 x - 3 ANSWER : x 2 + 4 x + 2 15) (2 x² - 5 x + 4) + (3 x² - 1) 13) 6 m² - 5 m + 3 (-) 5 m² + 2 m - 7 ANSWER : m 2 – 7 m + 10 ANSWER : 5 x 2 – 5 x + 3

- Slides: 10