Algebra I 1 4 Write Equations And Inequalities

Algebra I 1. 4 Write Equations And Inequalities

VOCAB Equation – a mathematical sentence formed by placing the symbol = between two expressions Inequality – a mathematical sentence formed by placing one of the symbols <, >, ≤, or ≥ between two expressions

VOCAB Open Sentence – an equation or inequality that contains an algebraic expression Solution to an Equation –a number that makes the sentence true Solution to an Inequality – a number or set of numbers that makes the sentence true

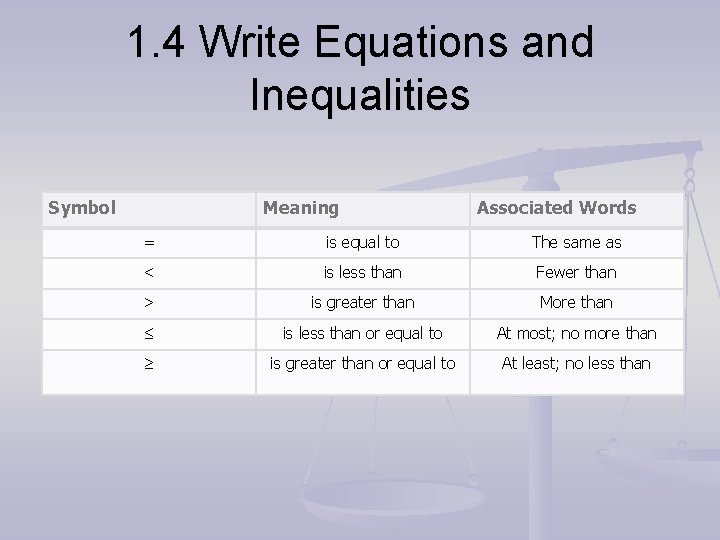
1. 4 Write Equations and Inequalities Symbol Meaning Associated Words = is equal to The same as < is less than Fewer than > is greater than More than ≤ is less than or equal to At most; no more than ≥ is greater than or equal to At least; no less than

1. 4 Write Equations and Inequalities n The BIG Difference n Equations: n Have ONLY ONE Solution! n Inequalities: n Have MANY Solutions!!!!!

EXAMPLE 1 Write equations and inequalities Verbal Sentence Equation or Inequality a. The difference of twice a number k and 8 is 12. 2 k – 8 = 12 b. The product of 6 and a number n is at least 24. 6 n ≥ 24

GUIDED PRACTICE for Example 1 c. A number y is no less than 5 and no more than 13. d. 5 ≤ y ≤ 13 Write an equation or an inequality: The quotient of a number p and 12 is at least 30. ANSWER P > 30 – 12

EXAMPLE 2 Check possible solutions Check whether 3 is a solution of the equation or inequality. Equation/Inequality Substitute Conclusion a. 8 – 2 x = 2 ? 2 8 – 2(3) = b. 4 x – 5 = 6 2=2 3 is a solution. 4(3) – 5 =? 6 c. 2 z + 5 > 12 7 = 6 X 3 is not a solution. 2(3) + 5 ? 12 11 > 12 X > 3 is not a solution. d. 5 + 3 n ≤ 20 ? 5 + 3(3) ≤ 20 14 ≤ 20 3 is a solution.

GUIDED PRACTICE for Example 2 Check to see whether or not 5 is a solution of the equation or inequality. Equation/Inequality Substitute Conclusion a. 9 – x = 4 9 – 5 ? = b. b + 5 < 15 ? 5 + 5 < 15 c. 2 n + 3 > – 21 ? X 2(5) + 3 > 21 – 21 13 > – 5 is NOT a solution. 4 4=4 5 is a solution. 10<15 5 is a solution.

EXAMPLE 3 Equation a. Use mental math to solve an equation Think Solution x + 4 = 10 What number Check 6 6 + 4 = 10 20 minus what number equals 8? 12 20 – 12 = 8 plus 4 equals 10? b. 20 – y = 8 c. 6 n = 42 6 times what number equals 42? 7 6(7) = 42 d. a =9 5 What number divided by 5 equals 9? 45 45 5 =9

GUIDED PRACTICE for Example 3 Solve the equation using mental math. Equation Think Solution Check 5. m + 6= 11 What number plus 6 equals 11? 5 5 + 6 = 11 6. 5 x = 40 5 times what number equals 40? 8 5(8) = 40 7. r = 10 4 What number divided by 4 equals 10 40 40 = 10 4

Is 2 a solution to 4 z – 5 < 3? 1. 2. A solution NOT a solution Answer Now

Solve for f: 1. 2. 3. 4. 0 12 24 4 Answer Now

EXAMPLE 4 Solve a multi-step problem Mountain Biking The last time you and 3 friends went to a mountain bike park, you had a coupon for $10 off and paid $17 for 4 tickets. What is the regular price of 4 tickets? If you pay the regular price this time and share it equally, how much does each person pay?

EXAMPLE 4 Solve a multi-step problem Step 1: Write a verbal model. Let p be the regular price of 4 tickets. Write an equation. Regular Price – Coupon = Amount Paid P – 10 = 17

EXAMPLE 4 Solve a multi-step problem Step 2: Use mental math to solve the equation p – 10 = 17. Think: 10 less than what number is 17? Because 27 – 10 = 17, the solution is 27. • Answer: The regular price for 4 tickets is $27. Step 3: Find Cost Person $27 / 4 people = 6. 75 • Answer: $6. 75 person.

GUIDED PRACTICE for Examples 4 and 5 WHAT IF? Suppose that the price of 4 tickets with a half-off coupon is $15. What is each person’s share if you pay full price?

GUIDED PRACTICE for Examples 4 and 5 STEP 1: Write a verbal model. Let p be the regular price of 4 tickets. Write an equation. Regular Price – Coupon = Amount Paid r – 15 = 15

GUIDED PRACTICE for Examples 4 and 5 STEP 2: Use mental math to solve the equation p – 15=15. Think: 15 less than what number is 15? Because 30 – 15 = 15, the solution is 30. So the full price is $30. STEP 3: Find the Cost Person $30/4 = 7. 5 Answer: $7. 50 person

EXAMPLE 5 Write and check a solution of an inequality STEP 1: Write a verbal model. Let p be the average number of points per game. Write an inequality. Number of Games • Number of Points Per Game > Total Points Last Year 18 • p > 351 STEP 2: Check that 20 is a solution of the in equality 18 p > 351. 18(20) = 360 > 351 Answer: An average of 20 points per game will be enough.

GUIDED PRACTICE for Examples 4 and 5 WHAT IF Suppose that the player plays 16 games. Would an average of 22 points per game be enough to beat last year’s total? STEP 1: Write a verbal model. Let p be the average number of points per game. Write an inequality. Number of Games • Number of Points Per Game = Total Points Last Year STEP 2: Check that 22 is a solution of the in equality 16 p > 351. Because 16(22) = 352 > 351 So, 22 is a solution.