ALGEBRA GRADO NOVENO SUMA Y DIFERENCIA DE CUBOS

ALGEBRA GRADO NOVENO SUMA Y DIFERENCIA DE CUBOS PERFECTOS SONIA LUCERO VANEGAS MARTINEZ I. E. D. PAULO VI

CUBOS PERFECTOS Es un número o término algebraico cuya raíz cubica es exacta Ejemplo: -8 es un cubo perfecto 3 -8 = -2 porque -23 =(-2)(-2) = -8 125 a 3 es cubo perfecto 3 125 a 3 = 5 a Porque (5 a) 3 = (5 a)(5 a) = 125 a 3 a 6 b 3 es cubo perfecto 3 a 6 b 3= a 2 b porque (a 2 b ) 3 = (a 2 b)(a 2 b) = a 6 b 3

DIFERENCIA DE CUBOS PERFECTOS Se le llama diferencia de cubos al binomio conformado por dos términos a los que se les puede sacar raíz cubica exacta. Ejemplo: 27 x 3 – y 3 a 3 – 64 b 3 1000 x 9 - y 6
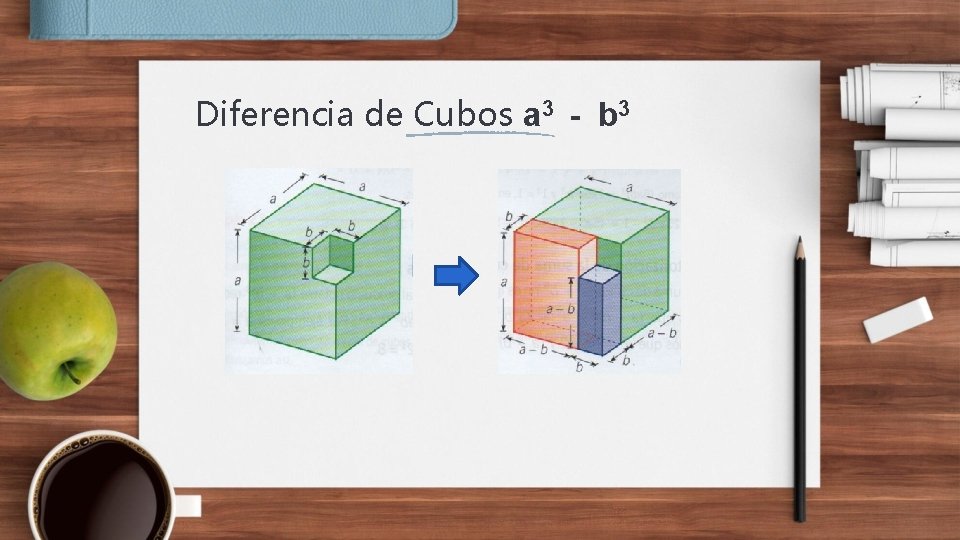
Diferencia de Cubos a 3 - b 3

a 3 - b 3 = V 1 + V 2 + V 3 V 1 = ab(a-b) V 2 = b 2 (a-b) V 3 = a 2 (a-b) a 3 - b 3 = ab (a-b) + b 2 (a-b) + a 2 (a-b) a 3 - b 3 = (a - b) (ab + b 2 + a 2)

Conclusión Organizando nos queda a 3 - b 3 = (a - b)(a 2 + ab + b 2) La diferencia de dos cubos perfectos equivale a multiplicar dos factores: El primero, un binomio formado por la diferencia de las raíces cúbicas de los términos; el segundo, un trinomio cuyos términos son el cuadrado de la primera raíz más el producto de las raíces más el cuadrado de la segunda raíz. x 3 - y 3 = (x - y)(x 2 + xy + y 2)

Ejemplo 1 Factorizar 27 x 3 – y 3 Para factorizar la diferencia de cubos se sigue este proceso 1. Se extrae la raíz cubica de cada término 3 27 x 3 = 3 x y 3 = y 2. Se expresa la diferencia de cubos como el producto de la diferencia de las raices por la suma de los cuadrados mas su producto ( 3 x - y ) ( 9 x 2 +3 xy +y 2 )

Ejemplo 2 Factorizar 1000 m 3 – n 6 1. Se extrae la raíz cúbica de cada término 3 1000 m 3 = 10 m 3 n 6 = n 2 2. Se expresa la diferencia de cubos como el producto de la diferencia de las raices por la suma de los cuadrados mas su producto ( 10 m - n 2 ) 100 m ( + 2 2 10 mn ) +n 4
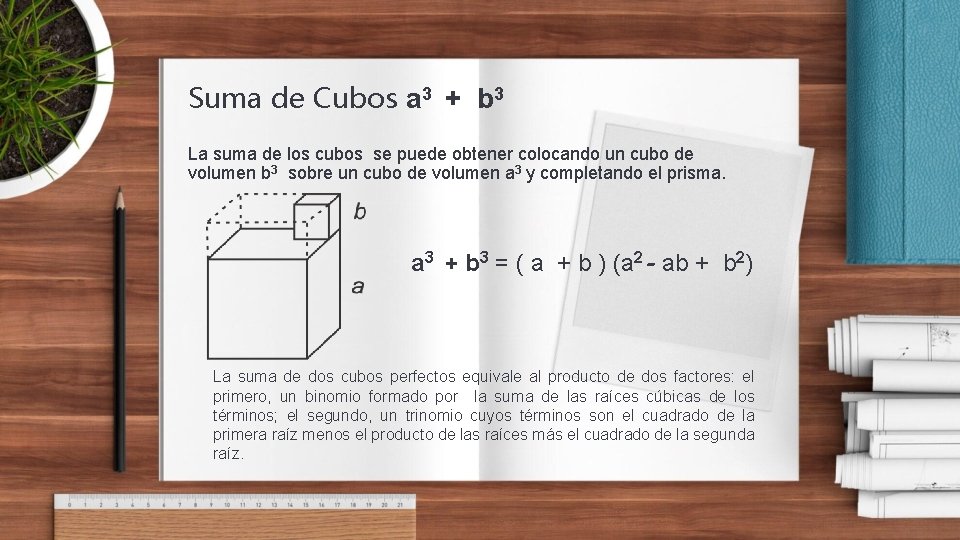
Suma de Cubos a 3 + b 3 La suma de los cubos se puede obtener colocando un cubo de volumen b 3 sobre un cubo de volumen a 3 y completando el prisma. a 3 + b 3 = ( a + b ) (a 2 - ab + b 2) La suma de dos cubos perfectos equivale al producto de dos factores: el primero, un binomio formado por la suma de las raíces cúbicas de los términos; el segundo, un trinomio cuyos términos son el cuadrado de la primera raíz menos el producto de las raíces más el cuadrado de la segunda raíz.

Ejemplo 3 Factorizar a 3 + 125 b 3 1. Se extrae la raíz cubica de cada término 3 a 3 = a 3 125 b 3 = 5 b 2. Se expresa la suma de cubos como el producto de la suma de las raíces por la suma de los cuadrados de las raíces menos su producto. (a ) + 5 b ) ( a 2 -5 ab + 25 b 2

Ejemplo 4 Factorizar m 6 + 216 n 3 1. Se extrae la raíz cubica de cada término 3 m 6 = m 2 3 216 n 3 = 6 n 2. Se expresa la suma de cubos como el producto de la suma de las raíces por la suma de los cuadrados de las raíces menos su producto. ( m 2 + 6 n ) ( m 4 ) -6 m 2 n + 36 n 2

ACTIVIDAD 1. Factorice las siguientes sumas o diferencias de cubos a) 64 x 3 – y 3 b) a 3 – 8 b 3 c) 1 + 343 y 3 d) m 6 – n 9 e) 27 x 6 + y 12 f) m 12 + 1
- Slides: 12