Algebra Generate and continue linear sequences Objectives Day

Algebra Generate and continue linear sequences Objectives Day 1 Generate and describe linear number sequences. Day 2 Generate and describe linear number sequences. Day 3 Generate and describe linear number sequences. © hamilton-trust. org. uk 1 Year 6

Algebra Generate and continue linear sequences Starters Day 1 Sequences (pre-requisite skills) Suggested for Day 2 Co-ordinates in 4 quadrants (simmering skills) Suggested for Day 3 Parts of circles (simmering skills) © hamilton-trust. org. uk 2 Year 6
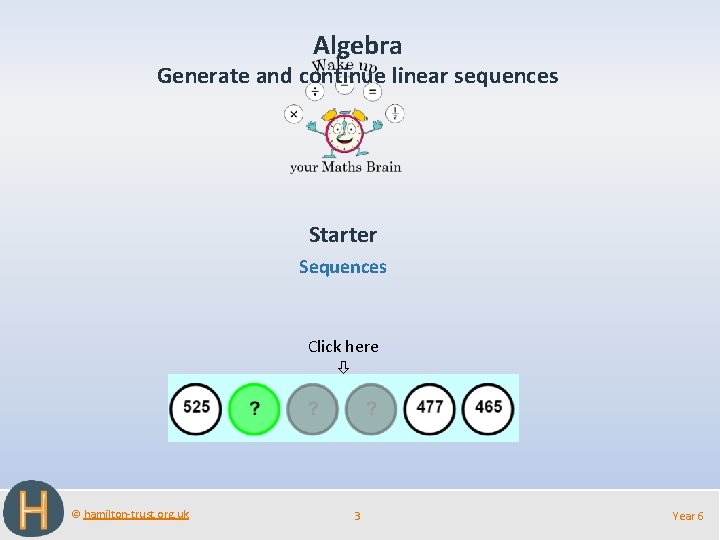
Algebra Generate and continue linear sequences Starter Sequences Click here © hamilton-trust. org. uk 3 Year 6

Algebra Generate and continue linear sequences Starter Co-ordinates in 4 quadrants Click here for ITP © hamilton-trust. org. uk 4 Year 6

Algebra Generate and continue linear sequences Starter Parts of circles © hamilton-trust. org. uk 5 Year 6

Algebra Generate and continue linear sequences Objectives Day 1 Generate and describe linear number sequences. © hamilton-trust. org. uk 6 Year 6

Day 1: Generate and describe linear number sequences. _ , _ , 24, _ , 36, _ , _ In this sequence the numbers go up by the same number each time. How can you figure out the steps and the missing numbers? What clues do you have? How many steps are between 24 and 36 in the sequence? Work in pairs to find the missing numbers. What is each step worth? Count up, then down to check. Write the complete sequence on your whiteboards to show me. © hamilton-trust. org. uk 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 7 Year 6

Day 1: Generate and describe linear number sequences. _ , 16, _ , 30, _ , _ , _ Work in pairs to find the missing numbers. What is each step worth? Count up, then down to check. Write the complete sequence on your whiteboards to show me. 2, 9, 16, 23, 30, 37, 44, 51, 58, 65 © hamilton-trust. org. uk 8 Year 6

Day 1: Generate and describe linear number sequences. _ , _ , 21, _ , 15, _ , _ This time the sequence is decreasing rather than increasing. Work in pairs to find the missing numbers. What is each step worth? Count along the sequence to check. Write the complete sequence on your whiteboards to show me. Describe the sequence. _ , _ , 26 , _ , 16, _ Work in pairs to find the missing numbers. What is each step worth? Count along the sequence to check. Write the complete sequence on your whiteboards to show me. Describe the sequence. © hamilton-trust. org. uk 9 Year 6
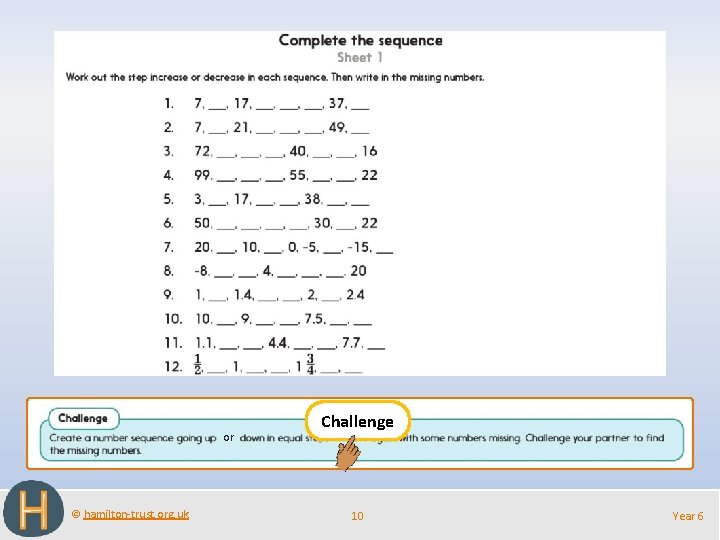
or © hamilton-trust. org. uk Challenge 10 Year 6

Algebra Generate and continue linear sequences Objectives Day 2 Generate and describe linear number sequences. © hamilton-trust. org. uk 11 Year 6

Day 2: Generate and describe linear number sequences. 2, 4, 6, 8 … • What is the next ‘term’ in this sequence? • What is the 10 th term? • And the 100 th? How did you work it out? You did not have time to count on in 2 s to 200! We can double 10 to find the 10 th term or double 100 to find the 100 th term. • So how can we find the nth term? The nth term is 2 n: double the number of the term. © hamilton-trust. org. uk 12 Year 6

Day 2: Generate and describe linear number sequences. 3, 6, 9, 12 … • What is the next term in this sequence? • What is the 10 th term? • And the 100 th? How did you work it out? We can multiply 10 by 3 to find the 10 th term and multiply 100 by 3 to find the 100 th term. • So how can we find the nth term? The nth term is 3 n: three times the number of the term. © hamilton-trust. org. uk 13 Year 6

Day 2: Generate and describe linear number sequences. 4, 7, 10, 13, 16 … • Talk to your partner about what the 10 th term might be, this is a little more difficult. It is 1 more than the 10 th term in the last sequence, i. e. 31. • What do you think 100 th term will be? 3 x 100, + 1, i. e. 301 • Talk to your partner about how you could find any term in this sequence. We can multiply the number of the term by 3 and then add 1. • How can we write this using n? 3 n + 1 This is a short way of recording how to find any term. © hamilton-trust. org. uk 14 Year 6

Day 2: Generate and describe linear number sequences. 5, 9, 13, 17, 21… • Talk to your partner about what the 10 th term might be. It is 1 more than the 10 th term in the sequence of multiples of 4, i. e. . 41. • What do you think 100 th term will be? 4 x 100, + 1, i. e. 401 • Talk to your partner about how you could find any term in this sequence. We can multiply the number of the term by 4 and then add 1. • How can we write this using n? 4 n + 1 This is a short way of recording how to find any term. © hamilton-trust. org. uk 15 Year 6
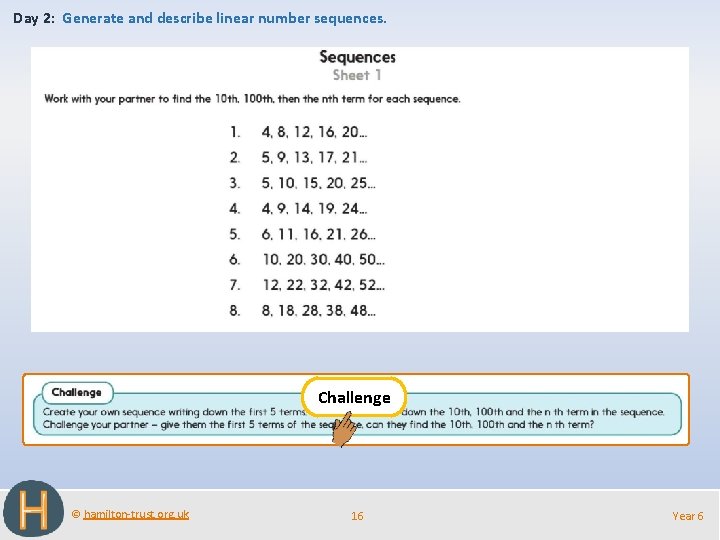
Day 2: Generate and describe linear number sequences. Challenge © hamilton-trust. org. uk 16 Year 6

Algebra Generate and continue linear sequences Objectives Day 3 Generate and describe linear number sequences. © hamilton-trust. org. uk 17 Year 6
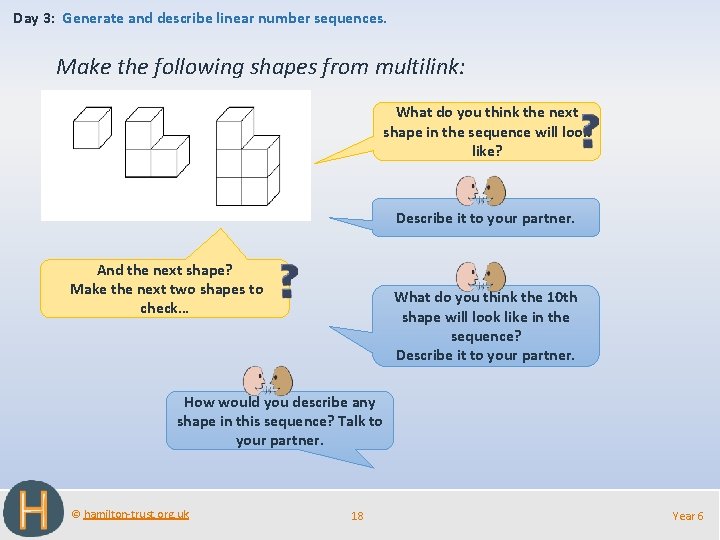
Day 3: Generate and describe linear number sequences. Make the following shapes from multilink: What do you think the next shape in the sequence will look like? Describe it to your partner. And the next shape? Make the next two shapes to check… What do you think the 10 th shape will look like in the sequence? Describe it to your partner. How would you describe any shape in this sequence? Talk to your partner. © hamilton-trust. org. uk 18 Year 6

Day 3: Generate and describe linear number sequences. Some people may see each shape as 2 towers, one with one more cube than the other. If you see it this way, how do you know how many cubes will be in each tower? The number in this tower is 1 less, n – 1. The number in this tower is the number of the term or shape in sequence, n. The number of cubes in any tower is n + n – 1, where n stands for the number of the term in the sequence. Some people may see each shape as a ‘rectangle’ with one cube taken out… If you see it this way, how do you know how big the rectangle is? It is 2 lots of the number of the term, and then 1 is subtracted. The number of cubes in any tower is 2 x n – 1. How can both these ways of seeing the shapes be correct? They are actually the same, because n + n – 1 = 2 n – 1, and 2 x n – 1 = 2 n – 1. © hamilton-trust. org. uk 19 Year 6

Day 3: Generate and describe linear number sequences. So let’s use our general expression and check. • If n is 10, 2 lots of 10 is 20, and then subtract 1 leaves 19, and this is what we said. • So how many will be in the 100 th shape? 2 x 100 – 1 = 199 • What will it look like? A tower of 100, and a tower of 99. 2 x 1000 – 1 = 1999 • How many in the 1000 th shape? • What will it look like? • And the millionth? • Once we have a general expression, we can work out how many cubes will be in any shape in the sequence, without working out all those before it! © hamilton-trust. org. uk 20 Year 6

Day 3: Generate and describe linear number sequences. Whole class investigation • Make these shapes from multilink: • Work in pairs to discuss how the number of cubes is growing, and predict how many might be in the 10 th shape. • Then come up with an expression for the nth term, and check this with several terms. How many cubes are in the 3 rd shape? The 10 th shape? What would the 20 th shape look like? So how many cubes would be in it? How many would be in the 100 th shape? 1000 th shape? So how many are in the nth shape? © hamilton-trust. org. uk 21 Year 6
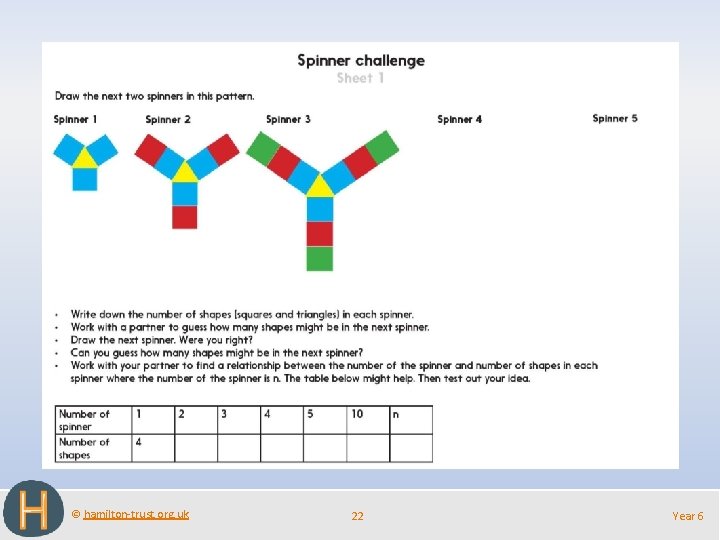
© hamilton-trust. org. uk 22 Year 6

Algebra Generate and continue linear sequences Well Done! You’ve completed this unit. Objectives Day 1 Generate and describe linear number sequences. Day 2 Generate and describe linear number sequences. Day 3 Generate and describe linear number sequences. © hamilton-trust. org. uk 23 Year 6

Algebra Problem solving and reasoning questions Three matches are arranged to make a triangle. How many more need to be added to make 2 triangles? How many more to make 3 triangles? Continue this sequence for 6 triangles. Write the number of matches that it takes to have 12 triangles. The fourth term of a sequence is 17, the fifth is 21 and the sixth is 25. Write the next four terms. Then write the first three terms. What is the general rule? Write the 10 th term in this sequence: 1. 5, 4. 5, 7. 5, 10. 5 … © hamilton-trust. org. uk 24 Year 6

Problem solving and reasoning answers Three matches are arranged to make a triangle. How many more need to be added to make 2 triangles? 2 more (5 in total). How many more to make 3 triangles? 2 more (7 in total). Continue this sequence for 6 triangles. Will need another 6 matches (13 in total). Write the number of matches that it takes to have 12 triangles. 25 The formula is 2 n + 1 where n is the number of triangles. The fourth term of a sequence is 17, the fifth is 21 and the sixth is 25. Write the next four terms. 29, 33, 37, 41 Then write the first three terms. 5, 9, 13 What is the general rule? 4 n + 1. Do children notice that the sequence of numbers is 1 more than the 4 times table? Write the 10 th term in this sequence: 1. 5, 4. 5, 7. 5, 10. 5 … 28. 5 Do any of the children spot that the rule for this sequence is based on 3 n (adding 3 each time; where the nth term of the sequence = 3 n – 1. 5. © hamilton-trust. org. uk 25 Year 6
- Slides: 25