Algebra Expressions Year 9 Note 1 Expressions We

Algebra Expressions Year 9

Note 1: Expressions We often use x to represent some number in an equation. We refer to the letter x as a variable. e. g. x + 5 means ‘a number with 5 added on’ x – 7 means ‘a number with 7 subtracted from it’

Note 1: Expressions A few Rules: A number should be written before a letter. e. g. y x 2 = 2 y Terms should be written in alphabetical order. e. g. xyz and 3 b x 4 a = 12 ab We don’t use the x or ÷ signs in algebra instead we write it like this: e. g. 5 x y = 5 y x ÷ 9 =

Activity: Expressions Match each algebraic expression with the phrase Five times a number x – 8 3 + x Three plus a number A number multiplied by seven Half of a number A number plus six 7 x 3 x + 1 5 x A number divided by nine A number minus eight Three times a number plus one x + 6

Activity: Expressions Write an equivalent algebraic expression for each phrase 12 x 1 + x Twelve times a number One plus a number A number multiplied by three 3 x A quarter of a number A number plus one hundred x + 100 A number divided by nineteen A number minus four x – 4 Eight times a number minus one 8 x – 1 IWB Ex 11. 01 Pg 275 -276

Note 2: Substitution • We replace the variable (letter) with a number and calculate the answer. • Algebra follows the same rules as BEDMAS! e. g. If a = 2, b = -3, c = 5 then calculate: a + 5 = 2 + 5 3 b = 3 x -3 = 7 = -9 a + b + c = 2 + -3 + 5 = 2 – 3 + 5 = 4

Note 2: Substitution Remember: Do multiplication and division before addition and subtraction Anything in brackets is worked out first A number in front of the bracket means multiply The fraction line means divide e. g. If d = 3, e = 7, f = -2 then calculate: 4(d + e) = 4(3 + 7) 5 def – 2 e = 5 x 3 x 7 x -2 – 2 x 7 = 4 x 10 = 40 = -210 – 14 = -224 = = = 4

Note 2: Substitution Remember: Do multiplication and division before addition and subtraction Anything in brackets is worked out first A number in front of the bracket means multiply The fraction line means divide e. g. If d = 3, e = 7, f = -2 then calculate: 2(d - e)2 = 2(3 - 7)2 = 2 x (-4)2 = 2 x 16 = 32 5 f – 2 d = 5 x -2 – 2 x 3 = -10 – 6 = -16 = = = 2

Note 2: Substitution e. g. Number of tyres = 5 x the number of cars b Number of tyres = 5 x 60 = 300 c 5 x 40 = 200 IWB Ex 11. 02 Pg 278 -280 Ex 11. 03 Pg 282 Puzzle Pg 283

Starter - = 5 x 3 = 15 = 5 x -4 = -20 = 3 x -4 = -12 = 2 x -4 = -8 = 12 x 3 = 36 = 2 x -4 = -8 = 6 x 2 = 3 x 2 = 6 = 3 x 2 x -4 = -24 = 12

Note 3: Formulas A formula is a mathematical rule that explains how to calculate some quantity. e. g. John baby sits for his neighbours. He charges a set fee of $10 plus $5 for every hour (h), that he baby sits. A formula to calculate this charge is given by: Charge = $10 + $5 h Use the formula to calculate the amount John charges if he baby sits for: 5 hours = 10 + 5 x 5 = $ 35 3 hours = 10 + 5 x 3 = $ 25

Note 3: Formulas e. g. If John receives $65 how long did he baby sit for? Charge = $10 + $5 h $65 = $10 + $5 x h 65 = 10 + 5 h 65 -10 = 10 -10 + 5 h 55 = 5 h 5 5 11 = h John baby sat for 11 hours IWB Ex 12. 01 Pg 299 -302 Ex 12. 02 Pg 305 -308

Starter Multiply the base length by the height and divide by 2 = 20 cm 2

Note 4: Multiplying Algebraic Expressions Rules: Multiply the numbers in the expression (these are written first) Write letters in alphabetical order

Note 5: Adding & Subtracting Algebraic Expressions Write in simplest form: y + y + y = 4 y a + a + a = 5 a a + a + a + b = 5 a + b a + a + a + b + b = 5 a + 3 b x + y + x = 4 x + 3 y x + y + y - x = 4 y

Note 5: Adding & Subtracting Algebraic Expressions Write in simplest form: y + 3 y = 4 y 3 x + 5 x = 8 x 5 x – 2 x + 3 x = 6 x 5 x – 4 x = x 10 x + 19 x = 30 x 12 p + 3 r – 2 p + 3 r = 10 p + 6 r IWB Ex 11. 05 Pg 285 Ex 11. 06 Pg 286

Note 6: Like and Unlike Terms Like terms are terms that contain the exact same variables (letters) or combinations of letters. e. g. Like Terms 2 x, 5 x, 25 x, -81 x, 13 x, 0. 5 x… xy, 2 xy, -4 xy, ½xy, -100 xy, … 2 abc, 4 bac, 6 cab, 9 abc, …. . Remember: If we had written these terms properly (in alphabetical order), it would be more obvious that they are like terms.

Note 6: Like and Unlike Terms Like terms are terms that contain the exact same variables (letters) or combinations of letters. e. g. Unlike Terms 2, 2 x, 3 y 3 a, 7 ab, 8 b 2 p, 4 r, 10 s

Note 6: Like and Unlike Terms Expressions can have a mixture of LIKE and UNLIKE terms. e. g. 3 x + 5 y 2 a – 7 b + 5 a + 8 b = 7 a + b Like terms can be grouped together and simplified Unlike terms cannot be simplified e. g. 5 a + 2 b – 3 a + 6 c + 4 b 2 a + 6 b + 6 c

Note 6: Like and Unlike Terms 2 x + 10 y 8 x + 8 y 4 x + 1 6 p + 9 q x + 1 2 x + 2 x 2 x – 7 IWB Ex 11. 07 Pg 289 Ex 11. 08 Pg 292 -3 Workbook Ex E page 117

Starter 1 2 x + 2 x + 3 x Find the perimeter of this shape in terms of x 4 x 2 – 5 x + 1 The perimeter is the sum of all side lengths P = x + (2 x + 1) + (2 x + 3) + (4 x + 1) + (5 x – 2) = 14 x + 3 If the perimeter is 31 cm. What is the value of x and which side is the longest? P = 14 x + 3 31 = 14 x + 3 28 = 14 x 14 14 x =2

Note 7: Powers (exponents) Recall: When a variable (letter) is multiplied by itself many times, we use powers e. g. Write the following in index form: p 3 p x p = ________ q x q x q = _____ q 5 s x s x t x t = _______ s 3 t 4 p 2 q 2 s 2 p x q x s x s = ____ s x t x t x s = _____ s 3 t 3

Note 7: Powers (exponents) Substituting: Evaluate the following when a =2, b = 7 and c = -3 a 2 = 22 = 4 (b + c)2 = (7 - 3)2 = (4)2 = 16 5 a 2 = 5 x 22 = 5 x 4 = 20 2 a 2 c 2 = 2 x 22 x (-3)2 = 2 x 4 x 9 (5 a)2 = (5 x 2)2 = 100 = 72

Note 7: Powers (exponents) NOTE: b = b 1 Multiplying: Simplify: b 3 x b 4 = (b x b) x (b x b x b) = b 7 When multiplying power expressions with the same base, we add the powers. e. g. e 2 x e 6 = e 2+6 = e 8 g 8 x g = g 8+1 = g 9 5 m 3 x 4 m 3 = 20 m 3+3 = 20 m 6

Note 7: Powers (exponents) Dividing: Simplify: = = c 3 IWB Ex 13. 08 Pg 346 Ex 13. 09 Pg 349 PUZZLE Pg 350 When dividing power expressions with the same base, we subtract the powers. e. g. = f 6 -3 = f 3 g 7 ÷ g = g 7 -1 = g 6 = 5 q 7 -3 = 5 q 4 =

Starter How would you calculate 7 x 83 in your head? 7 x 80 + 7 x 3 560 + 21 = 581 What we have done in our head can also look like this: x x 7 (80 + 3) = 7 x 80 + 7 x 3 = 581

Note 8: Expanding Brackets To expand (remove) brackets: – Multiply the outside term by everything inside the brackets – Simplify where possible e. g. Expand: a. ) 4(x + y) = 4 x + 4 y b. ) − 2(x – y) = -2 x + 2 y c. ) 5(x – y + 2 z) = 5 x - 5 y + 10 z The Distributive Law

Try These! e. g. Expand: a. ) 8(x + y) = 8 x + 8 y f. ) -8(x + y) = -8 x – 8 y b. ) 4(x – y) = 4 x - 4 y g. ) 5(x – 3 y) = 5 x – 15 y c. ) 2(x – y) = 2 x - 2 y h. ) -(x – 2 y) = -x + 2 y d. ) 3(-x + y) = -3 x + 3 y i. ) -7(-x + 7 y) = 7 x – 49 y e. ) 9(x + y + z) = 9 x + 9 y + 9 z j. ) -4(3 x - y + 5 z) = -12 x + 4 y – 20 z

Lets do some more e. g. Expand: a. ) 8(x + 4) = 8 x + 32 f. ) -8(x + 8) = -8 x – 64 b. ) 4(x – 2 y) = 4 x – 8 y g. ) 5(5 x – 3) = 25 x – 15 c. ) 2(x – 10) = 2 x - 20 h. ) -(x – 11) = -x + 11 d. ) 3(2 x + 9) = 6 x + 27 i. ) -7(x + 12) = -7 x – 84 e. ) -(x + 2 y - z) = -x – 2 y + z j. ) -2(x - y + 14) = -2 x + 2 y – 28

Note 8: Expanding Brackets The terms on the inside can also be multiplied by a variable on the outside. e. g. Expand: a. ) a(x + y) = ax + ay b. ) 2 a(a + b) = 2 a 2 + 2 ab c. ) 5 x 2(x 2 – x + 2) = 5 x 4 – 5 x 3 + 10 x 2

Your turn! e. g. Expand: a. ) a(x + 4) = ax + 4 a f. ) x 5(x 4+ x 3 y) = x 9 + x 8 y b. ) b(x – 5 y) = bx – 5 by g. ) 5 xy(3 xy – 1) = 15 x 2 y 2 – 5 xy c. ) x(x – 15) = x 2 – 15 x h. ) -x(x – 11) = -x 2 + 11 x d. ) y(2 x + 2) = 2 xy + 2 y e. ) x(x 2 + 2 y – 8) = x 3 – 2 xy – 8 x

Note 8: Expanding Brackets and Collecting Like Terms Expand the brackets first, then simplify! e. g. Expand & Simplify a. ) 4(2 x + y) + 3(x + 5 y) = 8 x + 4 y + 3 x + 15 y = 11 x + 19 y b. ) 4(5 x - y) – 3(x – 10) = 20 x - 4 y – 3 x + 30 = 17 x – 4 y + 30 * Collect like terms

Your turn! = 5 x + 5 y + 2 x + 2 y = 7 x + 7 y = 2 x + 2 y + 8 x + 4 y = 10 x + 6 y = 6 x + 3 y + 6 x + 12 y = 12 x + 15 y = 12 x + 18 y – 10 x – 4 y = 2 x + 14 y = 2 x + 6 + 4 x + 24 = 6 x + 30 IWB - odd only Ex 15. 02, 15. 03 Pg 389 Ex 15. 04 Pg 390 Ex 15. 05 Pg 391 Ex 15. 06, 15. 07 Pg 393 Ex 15. 08 Pg 397

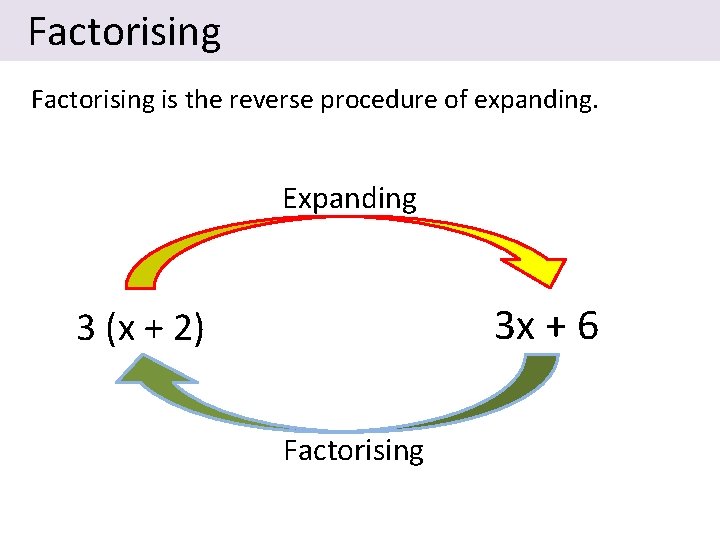
Factorising is the reverse procedure of expanding. Expanding 3 x + 6 3 (x + 2) Factorising

Note 9: Factorising (put in brackets) Factorising is the reverse process of expanding. • We want to put brackets back into the algebraic expression • find the highest common factor and write it in front of the brackets e. g. Factorise 3 x + 3 y = 3( ) x+y 4 x – 4 y = 4( ) x – y 7 x + 7 y + 7 z = 7( ) x + y + z

Try These e. g. Factorise: a. ) 6 a + 6 b = 6( ) a+b x+1 f. ) 7 x +7 = 7( ) b. ) 3 p – 3 q = 3( ) p – q x+2 g. ) 7 x + 14 = 7( ) x+y c. ) 4 x + 4 y = 4( ) h. ) 24 x + 36 = 12( ) 2 x+3 d. ) 6 x + 12 = 6( ) x+2 x+y e. ) 24 x + 24 y = 24( ) You can check that your answer is correct by expanding

Try These e. g. Factorise: a. ) 8 a + 6 b = 2( ) 4 a+3 b x+7 f. ) 7 x + 49 = 7( ) b. ) 12 p – 3 q = 3( ) 4 p – q x+7 g. ) 9 x + 63 = 9( ) c. ) 4 x + 8 = 4( ) x+2 h. ) 45 x + 81 = 9( ) 5 x+9 d. ) 6 x + 30 = 6( ) x+5 x+1 e. ) 29 x + 29 = 29( ) You can check that your answer is correct by expanding

Starter Factorise: a. ) 4 a + 8 b = 4(a+2 b) b. ) 3 p – 6 q + 3 r = 3(p – 2 q +r) c. ) 4 x + 8 y + 12 z = 4(x + 2 y + 3 z) d. ) 6 x + 21 = 3(2 x +7) e. ) 24 x - 32 = 8(3 x – 4) IWB - odd only Ex 15. 11 Pg 400 Ex 15. 13 Pg 401 Ex 15. 14 Pg 402 Ex 15. 15 Pg 403 Ex 15. 16 Pg 405

Extension – More exponent rules How do we simplify an exponential term raised to another exponent? × e. g. (2 y 3)2 × e. g. (3 a 4)3 = (2 y 3) × (2 y 3) = (3 a 4) × (3 a 4) = 4 y 6 = 27 a 12 Notice that there is a shortcut to get the same result = 22 y 2× 3 = 33 a 4× 3 = 4 y 6 = 27 a 12

Extension – More exponent rules 1. ) Index the number. 2. ) Multiply each variable index by the index outside the brackets. 3. ) If the bracket can be simplified, do this first. e. g. Simplify × (2 x 2)3 = 23 x 2 3 = 8 x 6 × (-4 h 2 g 6)2 = (-4)2 h 2× 2 g 6× 2 = 16 h 4 g 12 = (4 x)2 = 16 x 2

Extension – Expanding 2 Brackets QUADRATIC EXPANSION When we expand two brackets we use: F – first (multiply the first variable or number from each bracket) O – outside (multiply the outside variables together) I – inside (multiply the two inside variables together) L – last (multiply the last variable in each bracket together) Simplify, leaving your answer with the highest power first to the lowest power (or number) last. e. g. (x + 4) (x – 2) F O I L = x 2 - 2 x + 4 x - 8 = x 2 + 2 x - 8

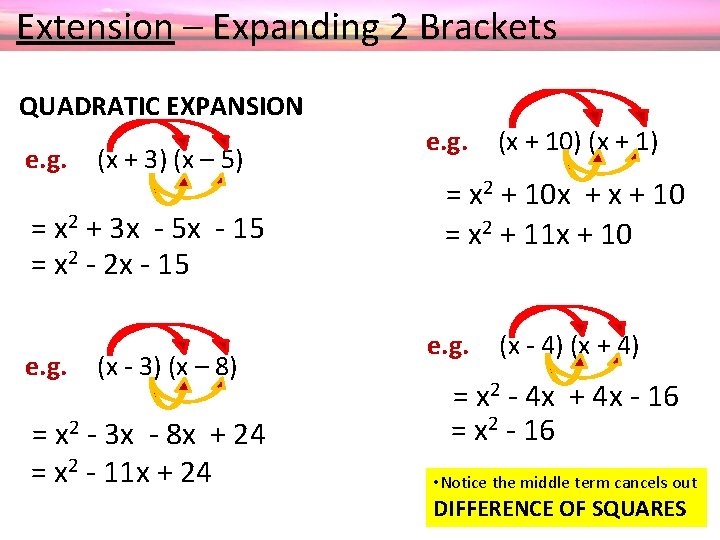
Extension – Expanding 2 Brackets QUADRATIC EXPANSION e. g. (x + 3) (x – 5) = x 2 + 3 x - 5 x - 15 = x 2 - 2 x - 15 e. g. (x - 3) (x – 8) = x 2 - 3 x - 8 x + 24 = x 2 - 11 x + 24 e. g. (x + 10) (x + 1) = x 2 + 10 x + 10 = x 2 + 11 x + 10 e. g. (x - 4) (x + 4) = x 2 - 4 x + 4 x - 16 = x 2 - 16 • Notice the middle term cancels out DIFFERENCE OF SQUARES

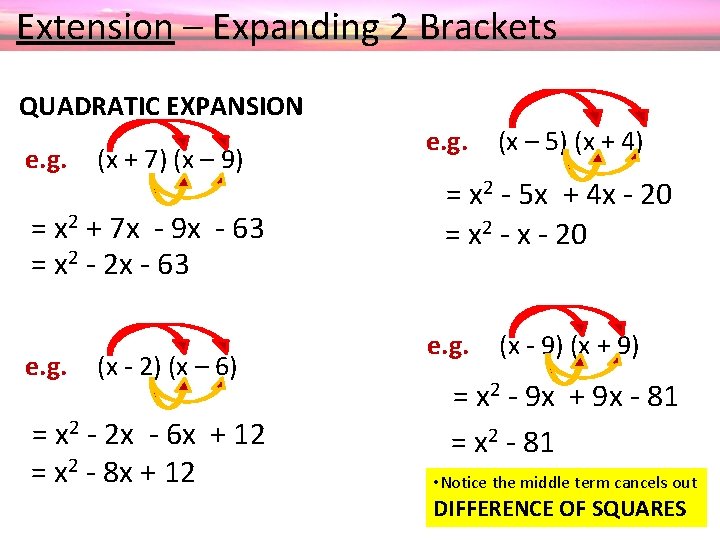
Extension – Expanding 2 Brackets QUADRATIC EXPANSION e. g. (x + 7) (x – 9) = x 2 + 7 x - 9 x - 63 = x 2 - 2 x - 63 e. g. (x - 2) (x – 6) = x 2 - 2 x - 6 x + 12 = x 2 - 8 x + 12 e. g. (x – 5) (x + 4) = x 2 - 5 x + 4 x - 20 = x 2 - x - 20 e. g. (x - 9) (x + 9) = x 2 - 9 x + 9 x - 81 = x 2 - 81 • Notice the middle term cancels out DIFFERENCE OF SQUARES

Extension – Factorising Quadratics e. g. Factorise simple quadratics: a. ) x 2 + 6 x + 8 (x+2) (x+4) b. ) x 2 - 5 x - 24 (x-8) (x+3) Find 2 numbers which multiply to 8 and add to 6 4 and 2 Put these number into brackets The factors are (x+2) and (x+4) Find 2 numbers which multiply to -24 and add to -5 -8 and 3 Put these number into brackets The factors are (x-8) and (x+3) c. ) x 2 + 5 x - 24 Find 2 numbers which multiply to -24 and add to 5 (x+8) (x-3) 8 and -3 Put these number into brackets