Algebra Ejemplos de Matrices Ramrez Abascal Guillermina Fabiola

Algebra Ejemplos de Matrices Ramírez Abascal Guillermina Fabiola. Grupo: 1241 Profesora: Ing. María Estela Gallegos Zarate.

Menú Tipos de matrices Determinantes Método Gauss Jordán

• Matriz fila Una matriz fila está constituida por una sola fila. • Matriz columna La matriz columna tiene una sola columna. • Matriz rectangular La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.

• Matriz cuadrada La matriz cuadrada tiene el mismo número de filas que de columnas. • Matriz nula En una matriz nula todos los elementos son ceros. • Matriz triangular superior En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros. • Matriz diagonal En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.

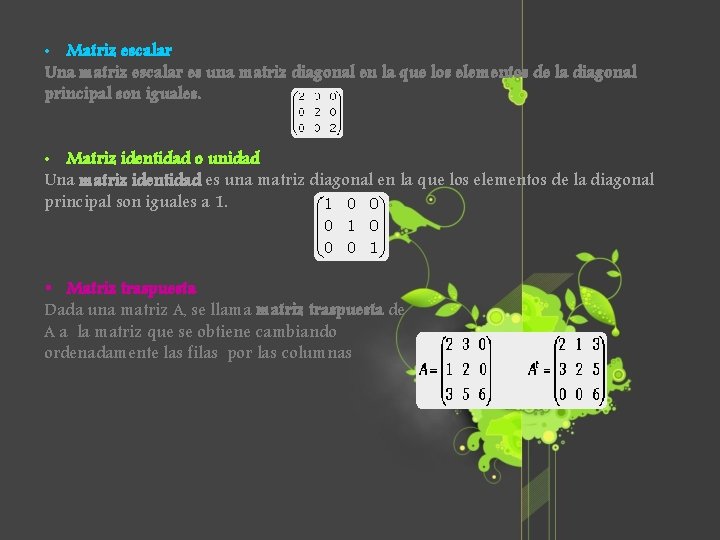
• Matriz escalar Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales. • Matriz identidad o unidad Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1. § Matriz traspuesta Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas

DETERMINANTES En una tienda de Abarrotes se compran 2 kg de Queso , 1 kg de Jamón y 2 kg de chorizo y se paga 200. Después compra 3 kg de Queso , 1 de Jamón y 2 kg de Chorizo y se paga 210. Y por ultimo se compran 2 kg de Queso , 1 kg de Jamón y 3 kg de chorizo y se paga 300. ¿Cuánto cuesta el kilo de cada producto? Ejemplo

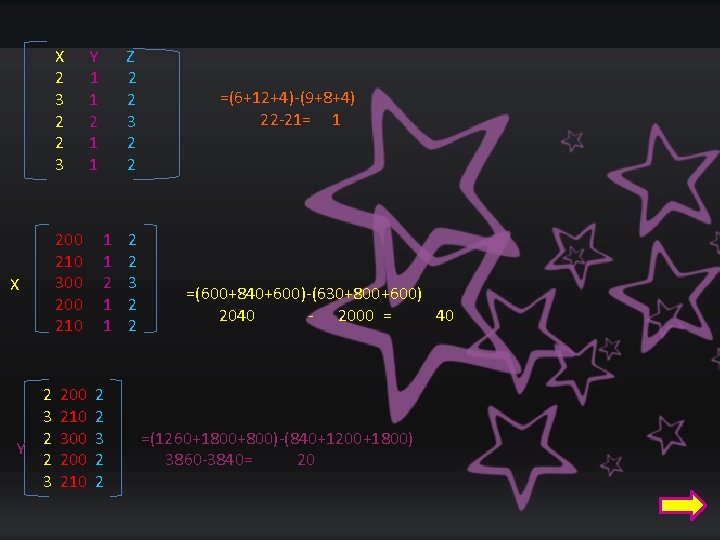
X 2 3 200 210 300 210 X Y 2 3 200 210 300 210 Y 1 1 2 1 1 Z 2 2 3 2 2 1 1 2 2 3 2 2 =(6+12+4)-(9+8+4) 22 -21= 1 =(600+840+600)-(630+800+600) 2040 - 2000 = 40 =(1260+1800+800)-(840+1200+1800) 3860 -3840= 20

Z 2 3 2 2 3 1 1 200 210 300 210 =(600+420+1200)-(900+840+400) 2220 -2140= 80 Los valores se obtienen al dividir el resultado de la Matriz y así se obtiene los resultados. X=40/1=40 Y=20/1=20 Z=80/1=80

Formula: La fila del pivote por el inverso , por el numero que se elimina , mas la fila del numero que quiero eliminar. fila(-2)+F 2 X+2 y=4 124 2 x+3 y=7 23 7 124 F 2(-2)+F 1 011 1=(-2)+2=0 2=(-2)+3=-1 F 2/2 4=(-2)+7=-1 Ejemplo 0 1 1 101 011 FI X=2 Y=1 0=(-2)+1=1 1=(-2)+2=0 1=(-2)+4=2

Tomaremos como pivote el elemento a 44=-3; multiplicamos la cuarta ecuación por y la restamos a la primera: Realizamos la misma operación con la segunda y tercera fila, obteniendo:

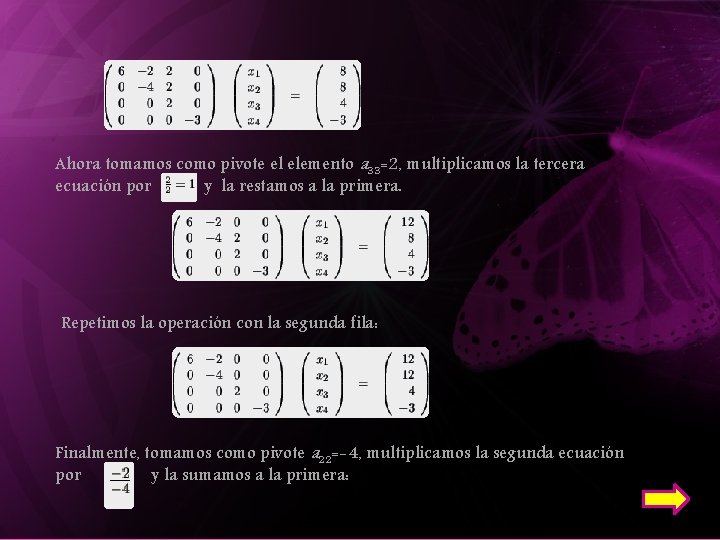
Ahora tomamos como pivote el elemento a 33=2, multiplicamos la tercera ecuación por y la restamos a la primera. Repetimos la operación con la segunda fila: Finalmente, tomamos como pivote a 22=-4, multiplicamos la segunda ecuación por y la sumamos a la primera:

El sistema de ecuaciones anterior es, como hemos visto, fácil de resolver. Empleando la ecuación (46) obtenemos las soluciones: Regresar a Menú