Algebra and Ratio Algebra Objectives Day 1 Begin

Algebra and Ratio Algebra Objectives Day 1 Begin to understand use simple formulae. Understand use simple formulae. Day 2 Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns, enumerate possibilities of combinations of two variables. Day 3 Generate and describe linear number sequences. Day 4 Generate and describe linear number sequences. © hamilton-trust. org. uk 1 Year 5/6

Algebra and Ratio Algebra Short Mental Workouts Day 1 Equivalence Day 2 Function machines Day 3 Counting back Day 4 Sequences © hamilton-trust. org. uk 2 Year 5/6

Algebra and Ratio Algebra Short Mental Workout Equivalence © hamilton-trust. org. uk 3 Year 5/6

Algebra and Ratio Algebra Short Mental Workout Function machines © hamilton-trust. org. uk 4 Year 5/6

Algebra and Ratio Algebra Short Mental Workout Counting back © hamilton-trust. org. uk 5 Year 5/6

Algebra and Ratio Algebra Short Mental Workout Sequences © hamilton-trust. org. uk 6 Year 5/6

Algebra and Ratio Algebra Objectives Day 1: Begin to understand use simple formulae. Understand use simple formulae. © hamilton-trust. org. uk 7 Year 5/6
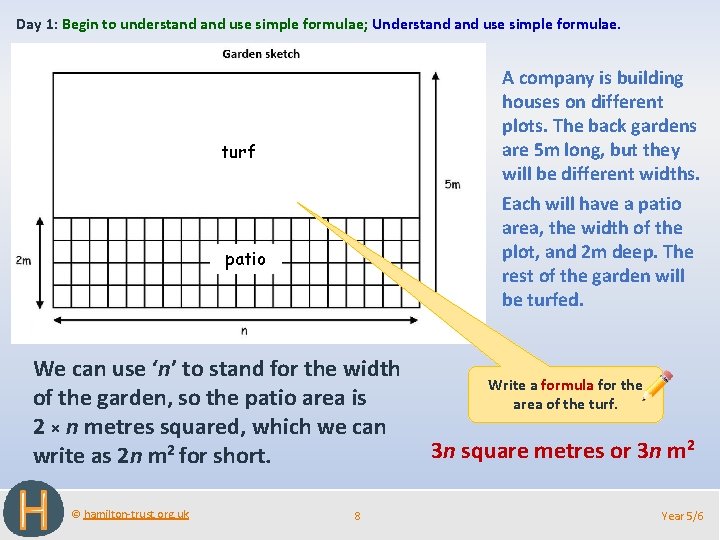
Day 1: Begin to understand use simple formulae; Understand use simple formulae. A company is building houses on different plots. The back gardens are 5 m long, but they will be different widths. Each will have a patio area, the width of the plot, and 2 m deep. The rest of the garden will be turfed. turf patio We can use ‘n’ to stand for the width of the garden, so the patio area is 2 × n metres squared, which we can write as 2 n m 2 for short. © hamilton-trust. org. uk 8 Write a formula for the area of the turf. 3 n square metres or 3 n m 2 Year 5/6
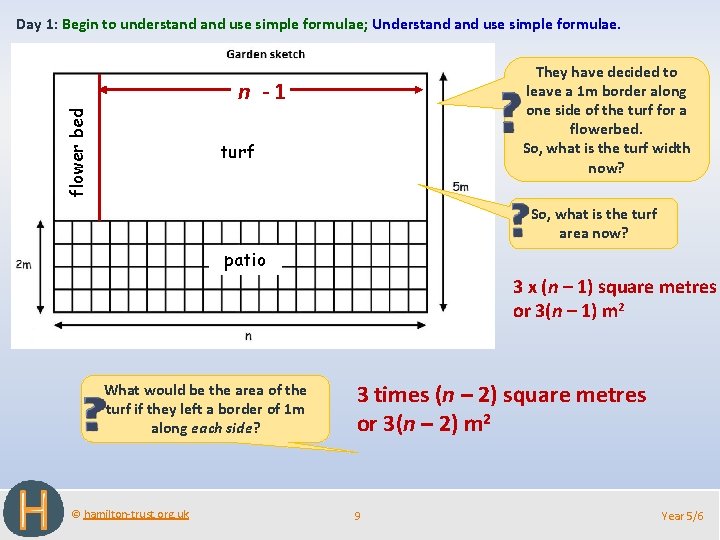
Day 1: Begin to understand use simple formulae; Understand use simple formulae. They have decided to leave a 1 m border along one side of the turf for a flowerbed. So, what is the turf width now? flower bed n -1 turf So, what is the turf area now? patio 3 x (n – 1) square metres or 3(n – 1) m 2 What would be the area of the turf if they left a border of 1 m along each side? © hamilton-trust. org. uk 3 times (n – 2) square metres or 3(n – 2) m 2 9 Year 5/6
Paste in ARE practice sheet for Year 5 © hamilton-trust. org. uk 10 Year 5/6

© hamilton-trust. org. uk 11 Year 5/6

Algebra and Ratio Algebra Objectives Day 2 Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. © hamilton-trust. org. uk 12 Year 5/6

Day 2: Express missing number problems algebraically; Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. 25 + a = 30 This is called an equation and ‘a’ stands for a mystery number. 25 30 What is a? a 6 b = 42 What is b? 42 b b b If 6 times something is 42, then the something must be… © hamilton-trust. org. uk 13 Year 5/6

Day 2: Express missing number problems algebraically; Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. 35 ÷ c = 7 c c c 35 c c c We can think of this as 7 lots of something makes 35. What is c? © hamilton-trust. org. uk c 14 Year 5/6
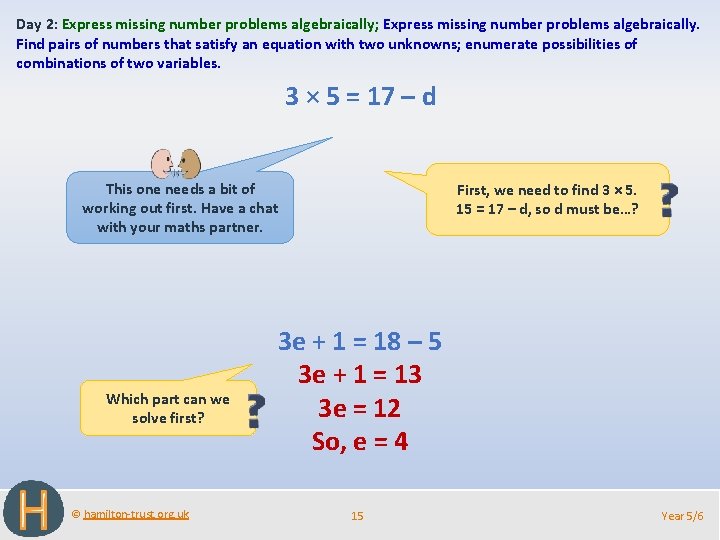
Day 2: Express missing number problems algebraically; Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. 3 × 5 = 17 – d This one needs a bit of working out first. Have a chat with your maths partner. Which part can we solve first? © hamilton-trust. org. uk First, we need to find 3 × 5. 15 = 17 – d, so d must be…? 3 e + 1 = 18 – 5 3 e + 1 = 13 3 e = 12 So, e = 4 15 Year 5/6

Day 2: Express missing number problems algebraically; Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. What is the total of the angles inside a triangle? How can we find a? a˚ 45˚ © hamilton-trust. org. uk 90˚ + 45˚ + a˚ = 180˚ 135˚ + a˚ = 180˚ So, a = 45˚ 90˚ 16 Year 5/6
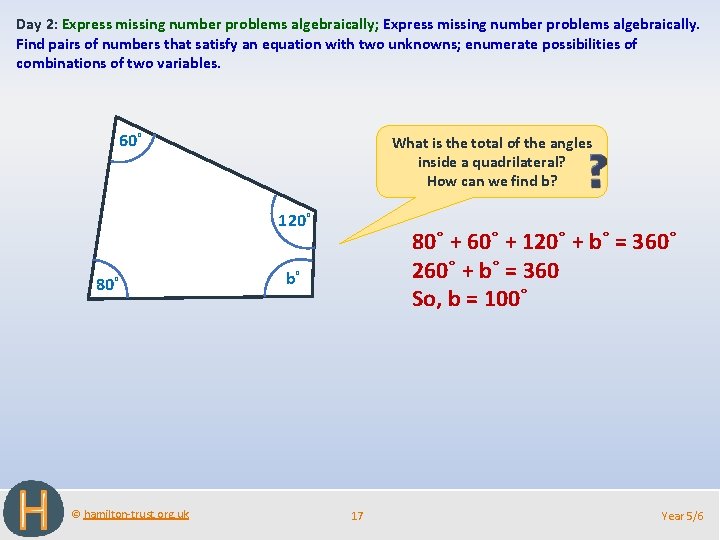
Day 2: Express missing number problems algebraically; Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. 60˚ What is the total of the angles inside a quadrilateral? How can we find b? 120˚ 80˚ © hamilton-trust. org. uk 80˚ + 60˚ + 120˚ + b˚ = 360˚ 260˚ + b˚ = 360 So, b = 100˚ b˚ 17 Year 5/6
© hamilton-trust. org. uk 18 Year 5/6

Day 2: Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. a + b = 10 a and b are positive whole numbers Discuss in pairs what numbers a and b might represent. There are LOTS of possibilities. List some pairs of possibilities. © hamilton-trust. org. uk 19 a b 10 0 9 1 8 2 7 3 6 4 5 5 4 6 3 7 2 8 1 9 0 10 Year 5/6
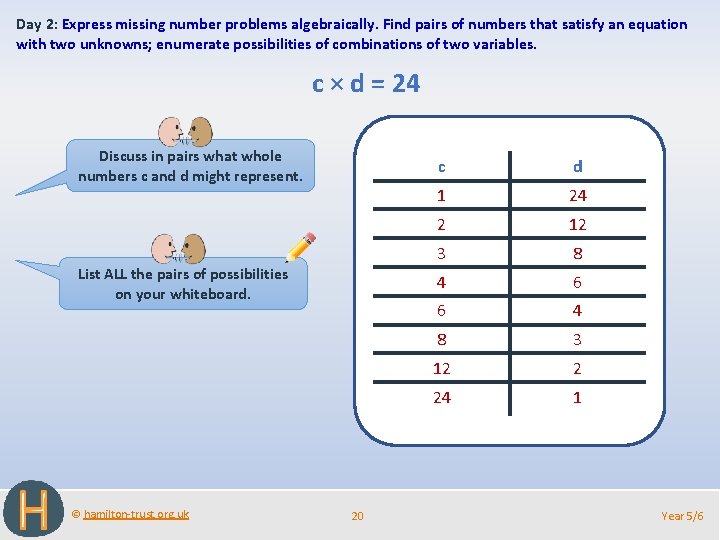
Day 2: Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. c × d = 24 Discuss in pairs what whole numbers c and d might represent. List ALL the pairs of possibilities on your whiteboard. © hamilton-trust. org. uk 20 c d 1 24 2 12 3 8 4 6 6 4 8 3 12 2 24 1 Year 5/6
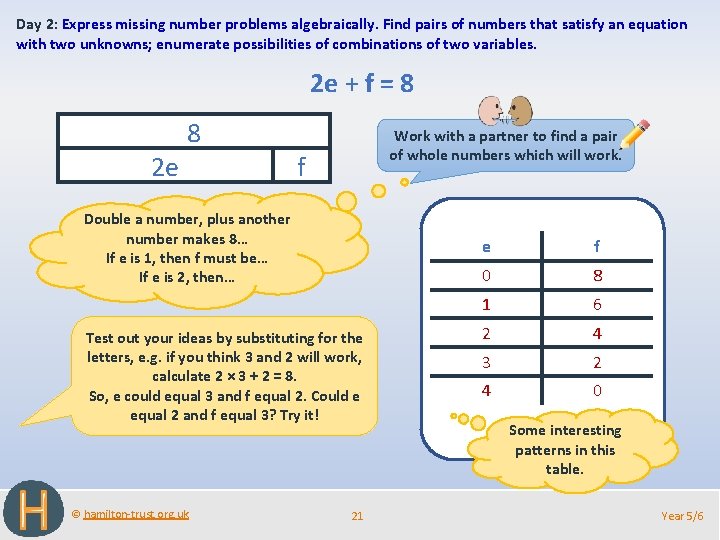
Day 2: Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns; enumerate possibilities of combinations of two variables. 2 e + f = 8 2 e 8 Work with a partner to find a pair of whole numbers which will work. f Double a number, plus another number makes 8… If e is 1, then f must be… If e is 2, then… Test out your ideas by substituting for the letters, e. g. if you think 3 and 2 will work, calculate 2 × 3 + 2 = 8. So, e could equal 3 and f equal 2. Could e equal 2 and f equal 3? Try it! © hamilton-trust. org. uk 21 e f 0 8 1 6 2 4 3 2 4 0 Some interesting patterns in this table. Year 5/6
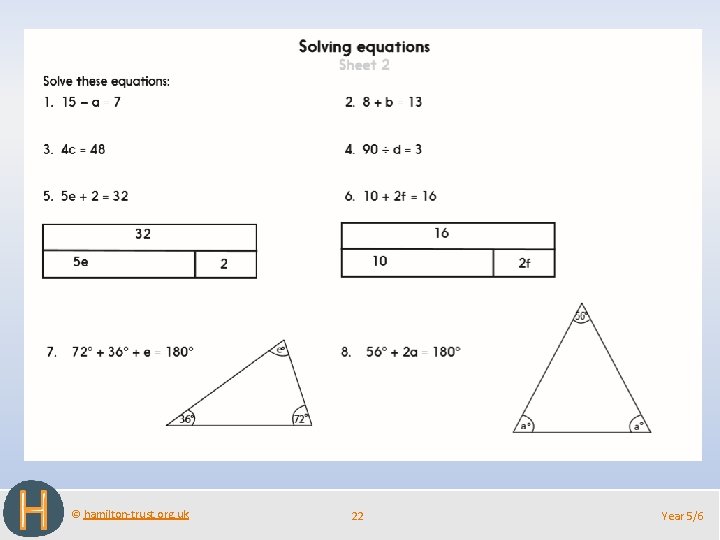
© hamilton-trust. org. uk 22 Year 5/6
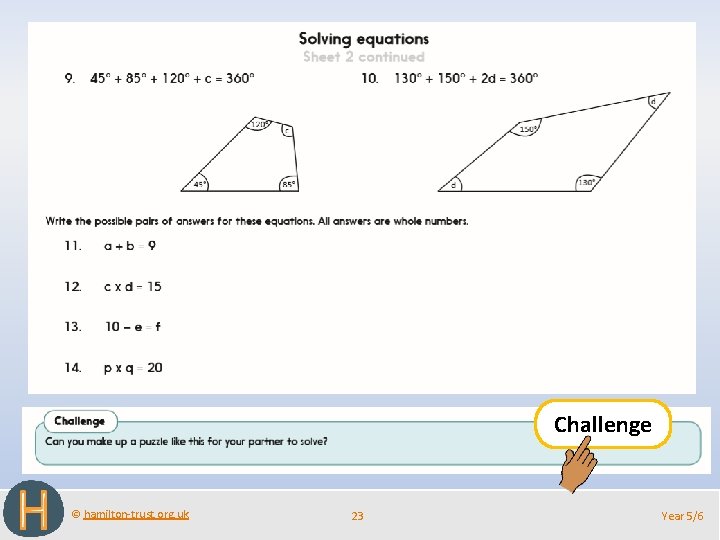
Challenge © hamilton-trust. org. uk 23 Year 5/6

Algebra and Ratio Algebra Objectives Day 3 Generate and describe linear number sequences. © hamilton-trust. org. uk 24 Year 5/6

Day 3: Generate and describe linear number sequences; Generate and describe linear number sequences. 2, 4, 6, 8 … • What is the next ‘term’ in this sequence? • What is the 10 th term? • And the 100 th? How did you work it out? You did not have time to count on in 2 s to 200! We can double 10 to find the 10 th term or double 100 to find the 100 th term. • So how can we find the nth term? The nth term is double the number of the term: 2 n. © hamilton-trust. org. uk 25 Year 5/6

Day 3: Generate and describe linear number sequences; Generate and describe linear number sequences. 1, 3, 5, 7… • What is the next ‘term’ in this sequence? And the nth? • We can put the results in a table number of term in sequence (n) 1 2 3 4 5 n value 1 3 5 7 9 ? • The values in this pattern also increase by 2 each time, but it’s not the 2 times table. How is it different? Describe what to do in words. How can you write that using n to represent any number? • 2 n – 1 Who can explain why that works? © hamilton-trust. org. uk 26 Year 5/6

Day 3: Generate and describe linear number sequences; Generate and describe linear number sequences. 3, 6, 9, 12 … • What is the next term in this sequence? • What is the 10 th term? • And the 100 th? How did you work it out? We can multiply 10 by 3 to find the 10 th term and multiply 100 by 3 to find the 100 th term. • So how can we find the nth term? The nth term is three times the number of the term: 3 n. © hamilton-trust. org. uk 27 Year 5/6

Day 3: Generate and describe linear number sequences; Generate and describe linear number sequences. 4, 7, 10, 13, 16 … • Talk to your partner about what the 10 th term might be. It is 1 more than the 10 th term in the last sequence, i. e. 31. • What do you think 100 th term will be? (3 × 100) + 1, i. e. 301 • Talk to your partner about how you could find any term in this sequence. We can multiply the number of the term by 3, then add 1. • How can we write this using n? 3 n + 1 We can use this formula to calculate the value of any term in the sequence. © hamilton-trust. org. uk 28 Year 5/6

Day 3: Generate and describe linear number sequences; Generate and describe linear number sequences. The number patterns you are looking at today are all sequences of numbers where the difference between each of the terms is the same. These are known as linear sequences. How do each of these sequences continue? Can you describe them algebraically using n for the nth term? 5, 10, 15, 20, 25… 4, 9, 14, 19, 24… 9, 16, 23, 30, 37… 1. 5, 5. 5, 9. 5, 13. 5, 17. 5 … © hamilton-trust. org. uk 29 Year 5/6
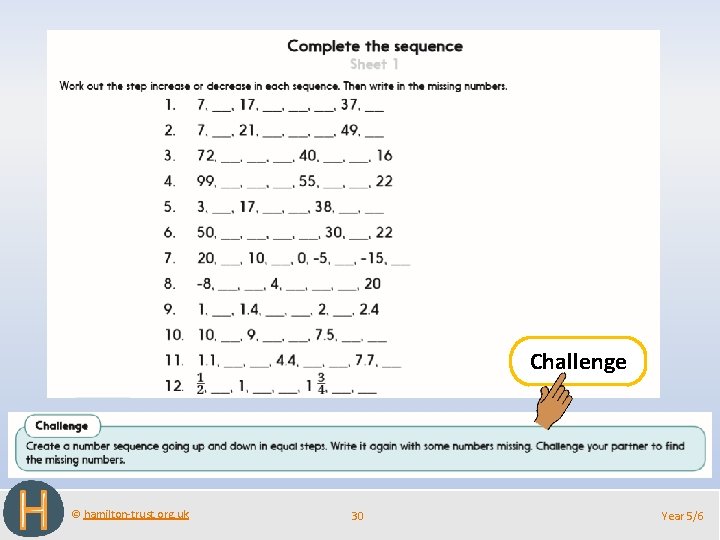
Challenge © hamilton-trust. org. uk 30 Year 5/6

Challenge © hamilton-trust. org. uk 31 Year 5/6

Algebra and Ratio Algebra Objectives Day 4 Generate and describe linear number sequences. © hamilton-trust. org. uk 32 Year 5/6
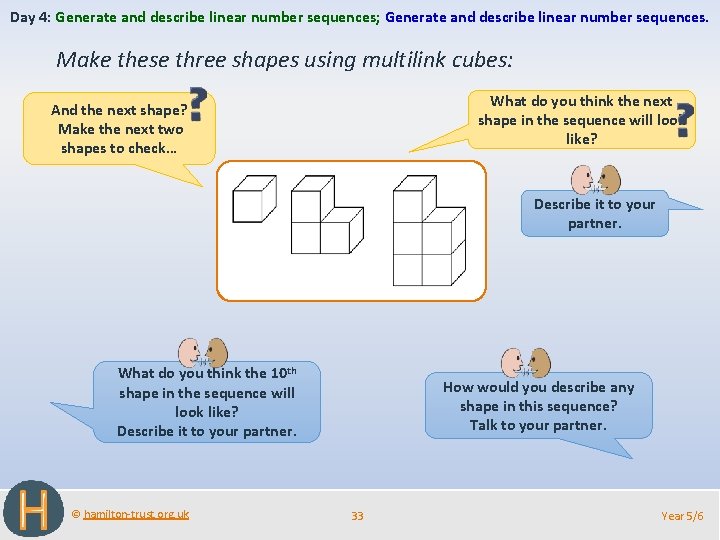
Day 4: Generate and describe linear number sequences; Generate and describe linear number sequences. Make these three shapes using multilink cubes: What do you think the next shape in the sequence will look like? And the next shape? Make the next two shapes to check… Describe it to your partner. What do you think the 10 th shape in the sequence will look like? Describe it to your partner. © hamilton-trust. org. uk How would you describe any shape in this sequence? Talk to your partner. 33 Year 5/6
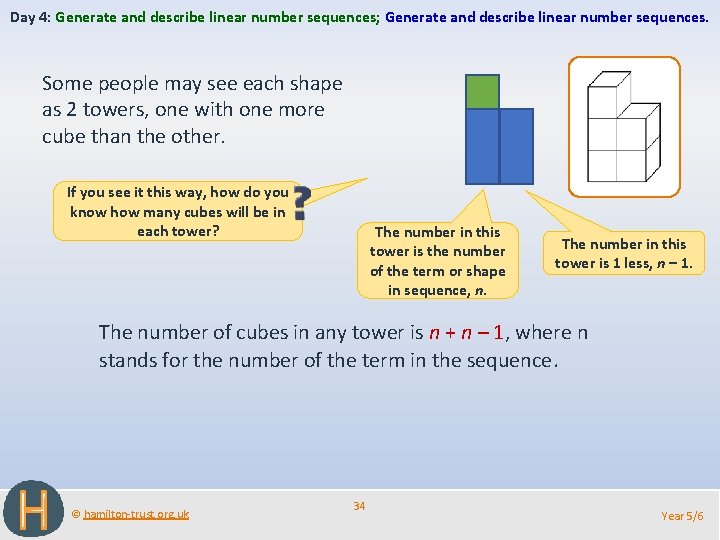
Day 4: Generate and describe linear number sequences; Generate and describe linear number sequences. Some people may see each shape as 2 towers, one with one more cube than the other. If you see it this way, how do you know how many cubes will be in each tower? The number in this tower is the number of the term or shape in sequence, n. The number in this tower is 1 less, n – 1. The number of cubes in any tower is n + n – 1, where n stands for the number of the term in the sequence. © hamilton-trust. org. uk 34 Year 5/6

Day 4: Generate and describe linear number sequences; Generate and describe linear number sequences. Some people may see each shape as a ‘rectangle’ with one cube taken out… If you see it this way, how do you know how big the rectangle is? It is 2 lots of the number of the term, and then 1 is subtracted. The number of cubes in any tower is 2 x n – 1. How can both these ways of seeing the shapes be correct? They are actually the same, because n + n – 1 = 2 n – 1, and 2 x n – 1 = 2 n – 1. © hamilton-trust. org. uk 35 Year 5/6

Day 4: Generate and describe linear number sequences; Generate and describe linear number sequences. So let’s use our general expression and check. • If n is 10, 2 lots of 10 is 20, and then subtract 1 leaves 19, and this is what we said. • So how many will be in the 100 th shape? 2 x 100 – 1 = 199 • What will it look like? A tower of 100, and a tower of 99. 2 x 1000 – 1 = 1999 • How many in the 1000 th shape? • What will it look like? • And the millionth? • Once we have a general expression, we can work out how many cubes will be in any shape in the sequence, without calculating all those before it! © hamilton-trust. org. uk 36 Year 5/6

Day 4: Generate and describe linear number sequences; Generate and describe linear number sequences. Y 6 Whole class investigation • Make these shapes from multilink: • In pairs, discuss what the 5 th shape would look like. • How tall will the 10 th shape be? How many cubes will be in it? • How tall will the 100 th shape be? How many cubes will be in it? • Then ask the same questions for this pattern of cubes: © hamilton-trust. org. uk 37 Year 5/6

Day 4: Generate and describe linear number sequences; Generate and describe linear number sequences. Y 6 Whole class investigation • Make these shapes from multilink: • In pairs, discuss how the number of cubes is growing, and predict how many might be in the 10 th shape. • Then try to write an expression for the nth term, and check this with several terms. How many cubes are in the 3 rd shape? The 10 th shape? What would the 20 th shape look like? So how many cubes would be in it? How many would be in the 100 th shape? 1000 th shape? So, how many are in the nth shape? © hamilton-trust. org. uk 38 Year 5/6
Challenge © hamilton-trust. org. uk 39 Year 5/6
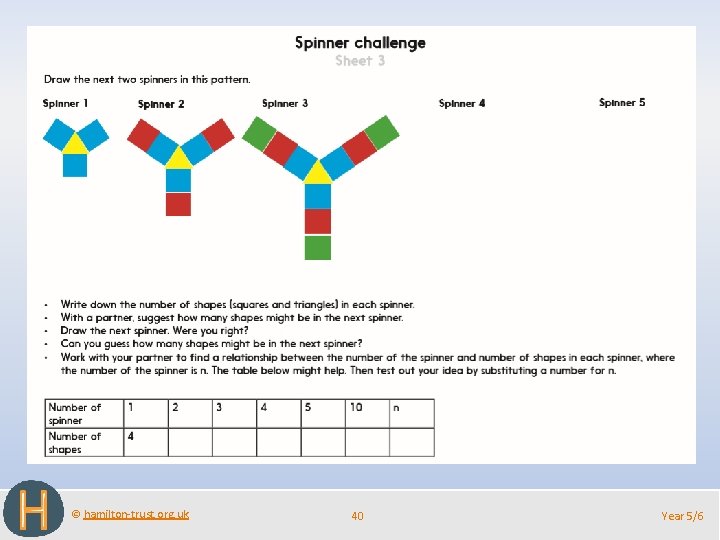
© hamilton-trust. org. uk 40 Year 5/6
Algebra and Ratio Algebra Well Done! You’ve completed this unit. Objectives Day 1 Begin to understand use simple formulae. Understand use simple formulae. Day 2 Express missing number problems algebraically. Find pairs of numbers that satisfy an equation with two unknowns, enumerate possibilities of combinations of two variables. Day 3 Generate and describe linear number sequences. Day 4 Generate and describe linear number sequences. © hamilton-trust. org. uk 41 Year 5/6

Problem solving and reasoning questions Year 5 & 6 If the perimeter of a regular shape is 5 × n, where n is the length of a side, what is the shape? Find the perimeter when n = 6. 5 cm. Darren draws a function machine. It trebles a number and then subtracts 6. Sophie sees that one of the outputs is 15. What was the input? Then Darren inputs 11. What output will Sophie see? Write the formula for Darren’s machine. Formula A is 3 n. Formula B is n + 6. What number can n represent which will make the two formulae equal the same amount? 2 a is 5 more than 3 b. If a and b are both whole numbers and a < 10, what are the possible values for a and b? The 4 th term of a sequence is 17, the 5 th is 21 and the 6 th is 25. Write the next four terms. Then write the first three terms. What is the nth term in this sequence? © hamilton-trust. org. uk 42 Year 5/6

Problem solving and reasoning answers Year 5 & 6 If the perimeter of a regular shape is 5 × n, where n is the length of a side, what is the shape? The shape is a pentagon. Find the perimeter when n = 6. 5 cm. 5 × 6. 5 = 32. 5 cm Darren draws a function machine. It trebles a number and then subtracts 6. Sophie sees that one of the outputs is 15. What was the input? 7 Use inverse operations to add 6 to 15, then divide by 3. Then Darren inputs 11. What output will Sophie see? 27 Write the formula for Darren’s machine. 3 n – 6. Formula A is 3 n. Formula B is n + 6. What number can n represent which will make the two formulae equal the same amount? n = 3. 2 a is 5 more than 3 b. If a and b are both whole numbers and a < 10, what are the possible values for a and b? Either a = 7 and b = 3 or a = 4 and b = 1. The 4 th term of a sequence is 17, the 5 th is 21 and the 6 th is 25. Write the next four terms. Then write the first three terms. What is the nth term in this sequence? 4 n + 1. Do children notice that the sequence of numbers is 1 more than the 4 times table? © hamilton-trust. org. uk 43 Year 5/6
- Slides: 43