Algebra 7 3 Solving Linear Systems by Linear

Algebra 7. 3 Solving Linear Systems by Linear Combinations

l This is the third and final way to solve linear systems. graphing l The other two are ______ substitution and _______.

Steps 1) 2) 3) 4) 5) Arrange the equations with like terms in columns. Multiply one or both equations by a number to obtain coefficients that are opposites for one variable. Add the equations. One variable will be eliminated. Solve for the other. Substitute this number into either original equation and solve for the other variable. Check.

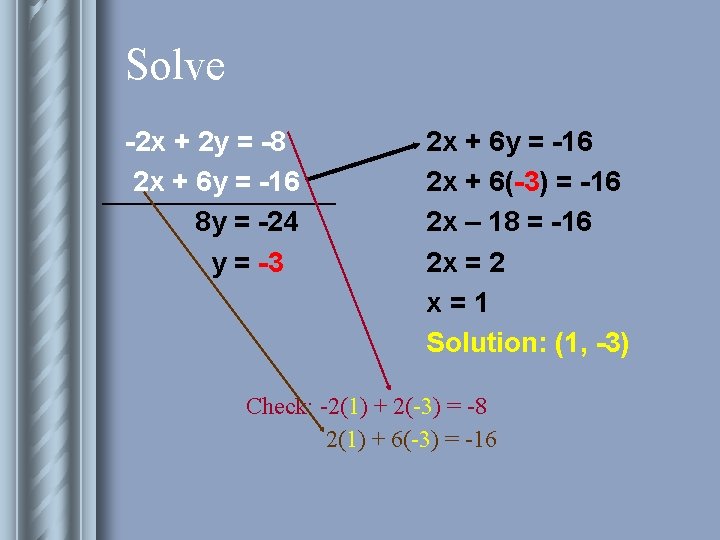
Solve -2 x + 2 y = -8 2 x + 6 y = -16 8 y = -24 y = -3 2 x + 6 y = -16 2 x + 6(-3) = -16 2 x – 18 = -16 2 x = 2 x=1 Solution: (1, -3) Check: -2(1) + 2(-3) = -8 2(1) + 6(-3) = -16

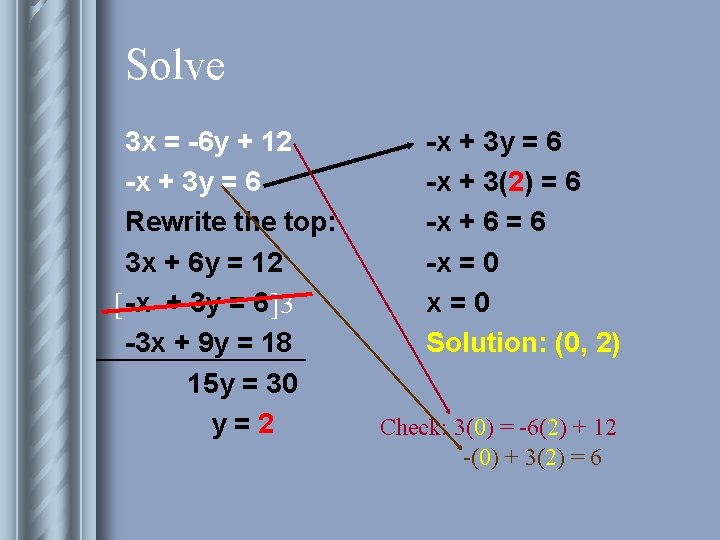
Solve 3 x = -6 y + 12 -x + 3 y = 6 Rewrite the top: 3 x + 6 y = 12 [ -x + 3 y = 6 ]3 -3 x + 9 y = 18 15 y = 30 y=2 -x + 3 y = 6 -x + 3(2) = 6 -x + 6 = 6 -x = 0 x=0 Solution: (0, 2) Check: 3(0) = -6(2) + 12 -(0) + 3(2) = 6

Solve 12 x + 20 y = 24 [ 3 x + 5 y = 6 ]4 [ -4 x + 2 y = 5 ]3 -12 x + 6 y = 15 26 y = 39/26 y = 3/2 -4 x + 2(3/2) = 5 -4 x + 3 = 5 -4 x = 2 x = -½ Answer: (-½, 3/2) Check: 12(-½) + 20(3/2) = 24 -4(-½) + 2(3/2) = 5

You try! Solve. 2 x + 8 y = -2 [ 5 x + 4 y = 3 ]-2 -10 x - 8 y = -6 -8 x = -8 x=1 2(1) + 8 y = -2 2 + 8 y = -2 8 y = -4 y = -½ Answer: (1, -½) Check: 2(1) + 8(-½) = -2 5(1) + 4(-½) = 3

A boat traveled from 24 miles downstream in 4 hours. It took the boat 12 hours to return upstream. Find the speed of the boat in still water(B) and the speed of the current(C). Speed in still water + current speed = speed downstream Speed in still water – current speed = speed upstream B + C = 6 mph B – C = 2 mph 2 B = 8 mph B = 4 mph The boat goes 4 mph + C = 6 mph C = 2 mph The current goes 2 mph. Speed downstream is 24 miles/4 hours = 6 mph Speed upstream is 24 miles/12 hours = 2 mph

HW P. 414 -415 (#9 -41 4 X) (#45 -48)