Algebra 2 Unit 2 Linear Relationships and Functions

Algebra 2 Unit 2: Linear Relationships and Functions Notes

1. 4—Solving Linear Equations • In your groups, discuss what you already know about the terms linear and equations.

Solving Equations • No matter how many steps are involved in solving equations, we have to remember our inverses: • The inverse of addition is subtraction. • The inverse of subtraction is addition. • The inverse of multiplication is division. • The inverse of division is multiplication.

One-Step Equations • With one-step equations, we only have to remember to do one inverse. • Example: 9 x = -90

Team Huddle • Complete the following problems in your groups. • 2 x = 14 • x – 11 = -9 • 18 + x = 13

Two-Step Equations • With two step equations, we have to add or subtract first. • Then we can multiply or divide. • Example: 7 x – 13 = 85

Team Huddle • Complete the following problems in your groups. • 8 x – 14 = 114 • 5 x + 22 = -28

Multi-Step Equations • With Multi-Step Equations, often times there are variables on both sides. • When this happens, simply pick what you want to get rid of first and then remember your inverses. • Example: 3 x + 2 = 6 x + 11

Team Huddle • Complete the following problem in your group: • 4 x + 12 = 8 x - 4

Distributive Property Equations • Remember from Unit 1 the rules of the distributive property. • Distributive Property Equations could see us having to do the property once or more than once. • Example: 2 (5 x – 6) = -4 x +16.

• Sometimes we have problems where one side cancels completely or everything cancels. • If we are solving an equation problem and we get 0=0, then our answer is an infinite number of solutions. • If we are solving an equation problem and we get 0=anything else, then our answer is no solution.

Team Huddle • Complete the following problem in your groups: • 8 (2 x + 18) = 0

1. 5—Rewriting Equations and Formulas • In your groups, write down as many math formulas as you can remember in two minutes.

• In your past math classes, you’ve had a goal of getting y by itself whenever you have worked with linear equations (whether it is graphing or writing) • You may be asked to take a variable and isolate it. This means you are trying to get it by itself.

Example • The formula for the perimeter of a rectangle is P = 2 l + 2 w • In this formula, P is isolated, l is the length, and w is the width. • What is the formula for l given the formula above?

Team Huddle • Given the formula A = lw, solve for w.

Calculating Variable Values • Given the equation 12 x + 4 y = 24, what is the value of x if y is 4. 5

Team Huddle • In your groups, find the value of y in the equation 3 x + 4 y = 10 when x = -2

Writing Equations with Two Variables • Example: A campus bookstore sells t-shirts for $15 each and sweatshirts for $22 each. Write an equation with more than one variable for the bookstore’s revenue R from selling m T-shirts and n sweatshirts. What does this algebraic model represent?

Solving Equations with Two Variables • Refer to our previous equation. Now lets assume that the bookstore made $6660 in revenue from sales of these two items. What is one possible combination of T-shirts and sweatshirts that will meet this objective?

1. 6—Problem Solving Using Algebraic Models • In your groups, huddle up and discuss the following scenario. • A recipe calls for 1 ½ cups of butter. However, you only have 2/3 cup of butter. How much more butter do you need?

• In looking at solving constructed response (openended) problems, the problem itself is known as a verbal model. • Our job is to convert a verbal model into an algebraic model.

Example • Chairlifts transport snowboarders and skiers to the tops of the ski runs. The Laurel Highlands Chairlift in Pennsylvania carries skiers a distance of 3250 feet. The chairlift moves at a speed of 450 feet per minute. Find the time it takes the chairlift to travel the entire distance.

Example • The table below gives the heights from the ground to the top of the first few stories of the Republic Plaza in Denver, Colorado. Determine the height from the ground to the top of the 9 th story. Story Lobby 2 3 4 Height (ft) 36 48. 5 61 73. 5

Team Huddle • Huddle up in your groups and solve the following: • The table shows the number of seats in each of the first four rows of an auditorium. The remaining 10 rows follow the same pattern. Determine how many seats are in the last row. Row 1 2 3 4 Seats 12 14 16 18

2. 3—Slope and Rate of Change • In your groups, talk about the following scenarios. Be ready to discuss. • A group of friends play a football game. • Then they climb up a mountain. • Then they ride roller coasters.

Slope • Slope—is the ratio of the line’s vertical change (rise) to its horizontal change (run). • It gives a measure of steepness. • Shown as the formula • This method would be used if we were given a graph with points.
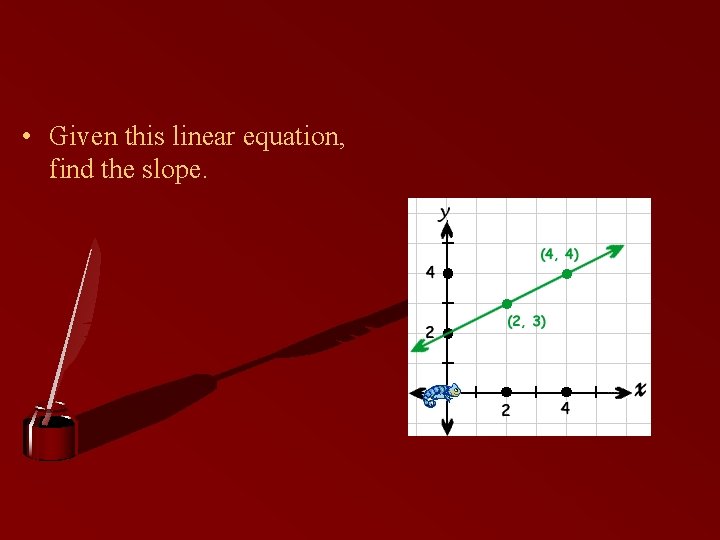
• Given this linear equation, find the slope.

Team Huddle • Given the linear equation, find the slope.

Slope Given Two Points • If we are given two points of a line as related to a coordinate plane, then we use the following formula:

Example • Find the slope of the line that goes through the points (-1, 5) and (3, 2).

Team Huddle • Find the slope that passes through the points (7, 4) and (8, 3)

Types of Slopes • Find the slope that passes through the point (4, 1) and (4, 3) • Find the slope that passes through the point (1, 4) and (3, 4) • What do you notice about these two problems?

• When given two points, if the x-values are the same, the slope is undefined. • When given two points, if the y-values are the same, the slope is zero.

Determining Which Line is Steeper • Whenever we look at the slopes of two lines, whichever number is bigger (in terms of its absolute value) is the steeper line. • Which line would be steeper, a line with slope -3 or a line with slope 2?

Team Huddle • Find the slope given the points (2, 5) and (-4, 1) • Find the slope given the points (-1, 6) and (4, 2) • Determine which line is steeper.

Slope as a Rate of Change • At 2: 00, the heated temperature of chocolate is 185 degrees. Fifteen minutes later, the temperature of the chocolate is 140 degrees. Find the average rate of change on the temperature of the chocolate.
- Slides: 37