Algebra 2 Standard Form of a Quadratic Function

Algebra 2 Standard Form of a Quadratic Function Lesson 4 -2 Part 1

Goals Goal • To graph quadratic functions written in standard form. Rubric Level 1 – Know the goals. Level 2 – Fully understand the goals. Level 3 – Use the goals to solve simple problems. Level 4 – Use the goals to solve more advanced problems. Level 5 – Adapts and applies the goals to different and more complex problems.

Vocabulary • Standard Form

Essential Question Big Idea: Function and Equivalence • Why is the standard form of a quadratic function useful?

Graphing a Quadratic Function in Standard Form • Two of the defining characteristics of a quadratic function are its vertex and axis of symmetry. • Therefore, when graphing a quadratic function, the first thing you want to calculate are the vertex and the axis of symmetry. • The vertex and axis of symmetry are related. The vertex is on the axis of symmetry and you can use the equation of the axis of symmetry to find the x -coordinate of the vertex.

Calculating the Properties of a Quadratic Function in Standard FORM 1. Axis of Symmetry 2. The Vertex 3. The y-Intercept

Review Axis of Symmetry The axis of symmetry is the line through the vertex of a parabola that divides the parabola into two congruent halves.

Standard Form Calculating the Axis of Symmetry You can use a formula to calculate the axis of symmetry. The formula works for all quadratic functions.

Standard Form Calculating the Axis of Symmetry Procedure: 1. Using the standard form of the quadratic function, y = ax 2 + bx + c, find the values of a and b. 2. Use the formula, . 3. Write the axis of symmetry as an equation.

Example: Find the axis of symmetry of the graph of y = – 3 x 2 + 10 x + 9. Step 1. Find the values of a and b. y = – 3 x 2 + 10 x + 9 a = – 3, b = 10 Step 3. Write as an equation. The axis of symmetry is Step 2. Use the formula.

Your Turn: Find the axis of symmetry of the graph of y = 2 x 2 + x + 3. Step 1. Find the values of a and b. y = 2 x 2 + 1 x + 3 a = 2, b = 1 Step 2. Use the formula. Step 3. Write as an equation. The axis of symmetry is .

Example: Find the vertex. y = – 3 x 2 + 6 x – 7 Step 1 Find the x-coordinate of the vertex. a = – 3, b = 10 Identify a and b. Substitute – 3 for a and 6 for b. The x-coordinate of the vertex is 1.

Example: Continued The x-coordinate of the vertex is 1. y = – 3 x 2 + 6 x – 7 Step 2 Find the corresponding y-coordinate. y = – 3 x 2 + 6 x – 7 = – 3(1)2 + 6(1) – 7 = – 3 + 6 – 7 = – 4 Step 3 Write the ordered pair. The vertex is (1, – 4). Use the function rule. Substitute 1 for x.

Your Turn: Find the vertex. y = x 2 – 4 x – 10 Step 1 Find the x-coordinate of the vertex. a = 1, b = – 4 Identify a and b. Substitute 1 for a and – 4 for b. The x-coordinate of the vertex is 2.

Continued The x-coordinate of the vertex is 2. y = x 2 – 4 x – 10 Step 2 Find the corresponding y-coordinate. y = x 2 – 4 x – 10 = (2)2 – 4(2) – 10 = 4 – 8 – 10 = – 14 Step 3 Write the ordered pair. The vertex is (2, – 14). Use the function rule. Substitute 2 for x.

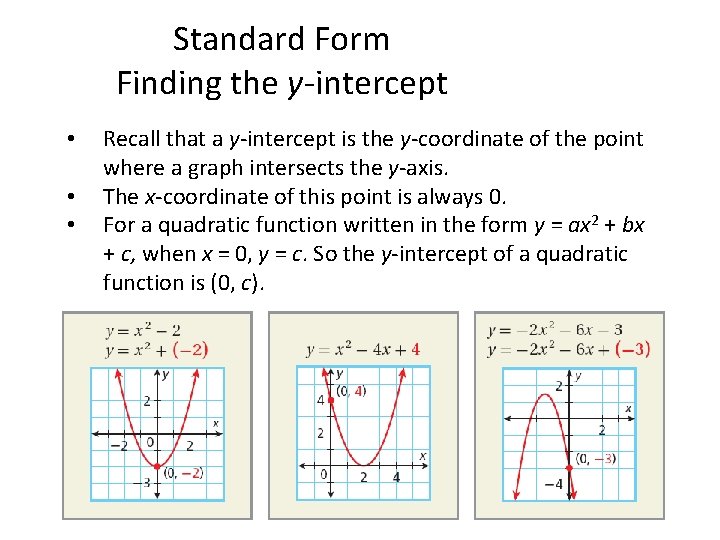
Standard Form Finding the y-intercept • • • Recall that a y-intercept is the y-coordinate of the point where a graph intersects the y-axis. The x-coordinate of this point is always 0. For a quadratic function written in the form y = ax 2 + bx + c, when x = 0, y = c. So the y-intercept of a quadratic function is (0, c).

Standard Form Graphing Quadratic Functions Procedure: 1. 2. 3. 4. Find the axis of symmetry, . Find the vertex, (h, k). Find the y-intercept. Find two more points on the same side of the axis of symmetry as the point containing the y-intercept. 5. Graph the axis of symmetry, the vertex, the point containing the y-intercept, and two other points. 6. Reflect the points across the axis of symmetry. Connect the points with a smooth curve. Confirm the direction the graph opens with the sign of a.

Example: Graph f(x) = 3 x 2 – 6 x + 1. Step 1 Find the axis of symmetry. Use x = . Substitute 3 for a and – 6 for b. =1 The axis of symmetry is x = 1. Step 2 Find the vertex. y = 3 x 2 – 6 x + 1 = 3(1)2 – 6(1) + 1 =3– 6+1 = – 2 The vertex is (1, – 2). Simplify. The x-coordinate of the vertex is 1. Substitute 1 for x. Simplify. The y-coordinate is – 2.

Example: Continued f(x) = 3 x 2 – 6 x + 1. Step 3 Find the y-intercept. y = 3 x 2 – 6 x + 1 Identify c. The y-intercept is 1; the graph passes through (0, 1).

Example: Continued f(x) = 3 x 2 – 6 x + 1. Step 4 Find two more points on the same side of the axis of symmetry as the point containing the y-intercept. Since the axis of symmetry is x = 1, choose x-values less than 1. Let x = – 1. y = 3(– 1)2 – 6(– 1) + 1 =3+6+1 = 10 Substitute x-coordinates. Simplify. Let x = – 2. y = 3(– 2)2 – 6(– 2) + 1 = 12 + 1 = 25 Two other points are (– 1, 10) and (– 2, 25).

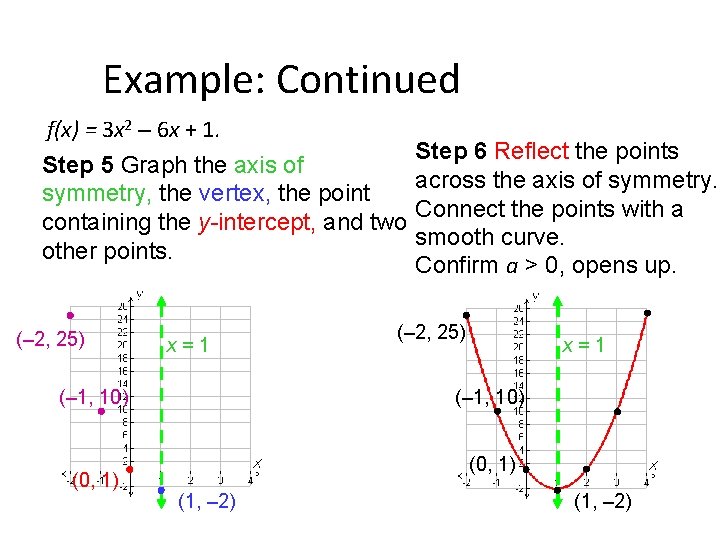
Example: Continued f(x) = 3 x 2 – 6 x + 1. Step 5 Graph the axis of symmetry, the vertex, the point containing the y-intercept, and two other points. (– 2, 25) x=1 (– 1, 10) (0, 1) Step 6 Reflect the points across the axis of symmetry. Connect the points with a smooth curve. Confirm a > 0, opens up. (– 2, 25) x=1 (– 1, 10) (0, 1) (1, – 2)

Example: Graph the quadratic function. f(x) = 2 x 2 + 6 x + 2 Step 1 Find the axis of symmetry. Use x = . Substitute 2 for a and 6 for b. Simplify. The axis of symmetry is x .

Continued f(x) = 2 x 2 + 6 x + 2 Step 2 Find the vertex. y = 2 x 2 + 6 x + 2 The x-coordinate of the vertex is. Substitute =4 – 9+2 Simplify. = – 2 The y-coordinate is The vertex is . for x. .

Continued f(x) = 2 x 2 + 6 x + 2 Step 3 Find the y-intercept. y = 2 x 2 + 6 x + 2 Identify c. The y-intercept is 2; the graph passes through (0, 2).

Continued f(x) = 2 x 2 + 6 x + 2 Step 4 Find two more points on the same side of the axis of symmetry as the point containing the y-intercept. Since the axis of symmetry is x = – 1 , choose x values greater than – 1 . Let x = – 1 y = 2(– 1)2 + 6(– 1) + 1 =2– 6+2 = – 2 Let x = 1 Substitute x-coordinates. Simplify. Two other points are (– 1, – 2) and (1, 10). y = 2(1)2 + 6(1) + 2 =2+6+2 = 10

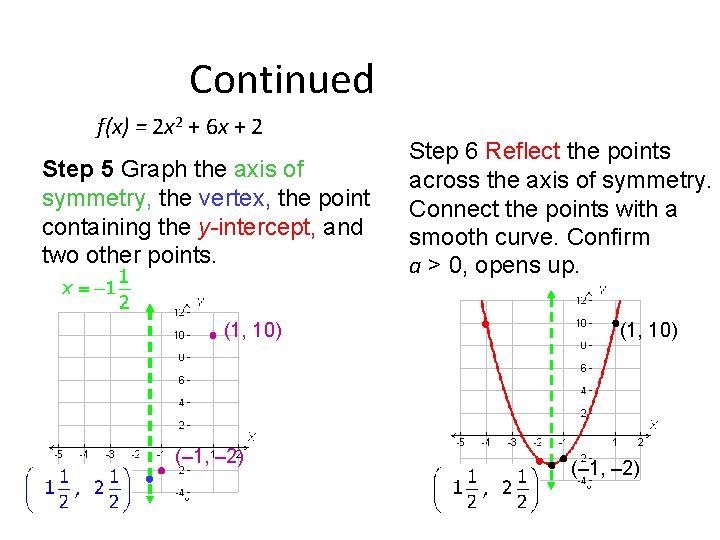
Continued f(x) = 2 x 2 + 6 x + 2 Step 5 Graph the axis of symmetry, the vertex, the point containing the y-intercept, and two other points. (1, 10) (– 1, – 2) Step 6 Reflect the points across the axis of symmetry. Connect the points with a smooth curve. Confirm a > 0, opens up. (1, 10) (– 1, – 2)

Your Turn: Graph the quadratic function. y + 6 x = x 2 + 9 f(x) = x 2 – 6 x + 9 Rewrite in standard form. Step 1 Find the axis of symmetry. Use x = . Substitute 1 for a and – 6 for b. =3 The axis of symmetry is x = 3. Simplify.

Continued f(x) = x 2 – 6 x + 9 Step 2 Find the vertex. y = x 2 – 6 x + 9 y= 32 – 6(3) + 9 The x-coordinate of the vertex is 3. Substitute 3 for x. = 9 – 18 + 9 Simplify. =0 The y-coordinate is 0. The vertex is (3, 0). .

Continued f(x) = x 2 – 6 x + 9 Step 3 Find the y-intercept. y = x 2 – 6 x + 9 Identify c. The y-intercept is 9; the graph passes through (0, 9).

Continued f(x) = x 2 – 6 x + 9 Step 4 Find two more points on the same side of the axis of symmetry as the point containing the y- intercept. Since the axis of symmetry is x = 3, choose x-values less than 3. Let x = 2 y = 1(2)2 – 6(2) + 9 = 4 – 12 + 9 =1 Substitute x-coordinates. Simplify. Two other points are (2, 1) and (1, 4). Let x = 1 y = 1(1)2 – 6(1) + 9 =1– 6+9 =4

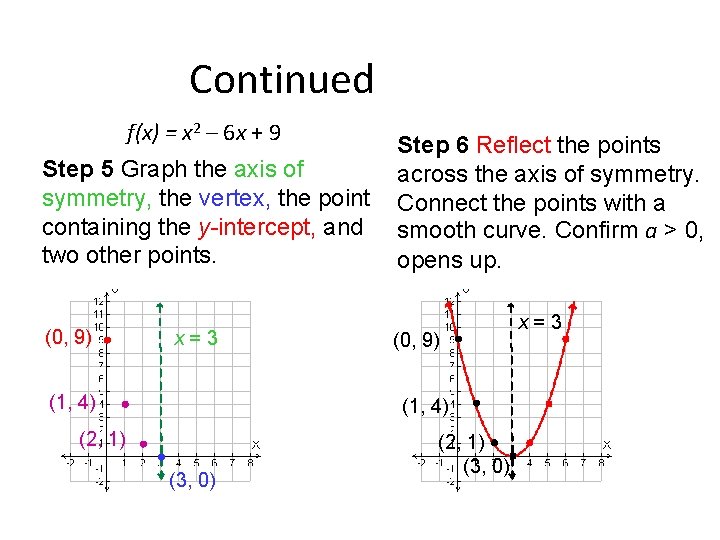
Continued f(x) = x 2 – 6 x + 9 Step 5 Graph the axis of symmetry, the vertex, the point containing the y-intercept, and two other points. (0, 9) x=3 (1, 4) Step 6 Reflect the points across the axis of symmetry. Connect the points with a smooth curve. Confirm a > 0, opens up. (0, 9) (1, 4) (2, 1) (3, 0) x=3

Assignment • Section 4 -2 pt 1, Pg. 214 – 215; #6 -18