Algebra 2 7 7 Inverse Relations and Functions

Algebra 2 7 -7 Inverse Relations and Functions

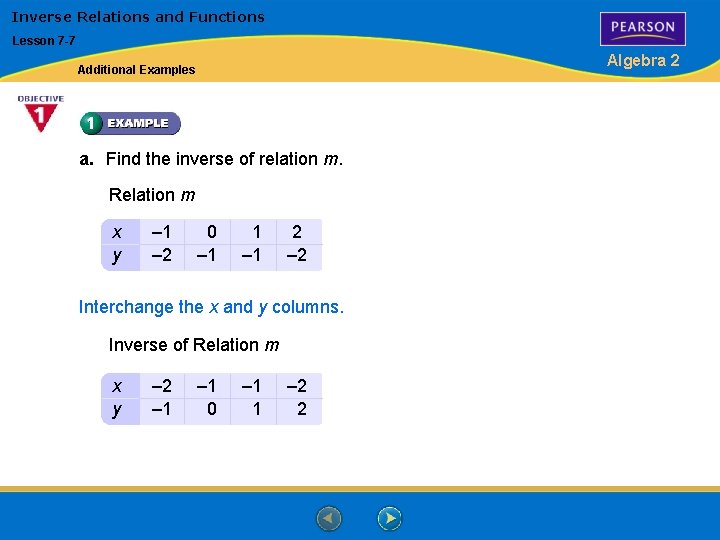
Inverse Relations and Functions Lesson 7 -7 Algebra 2 Additional Examples a. Find the inverse of relation m. Relation m x y – 1 – 2 0 – 1 1 – 1 2 – 2 Interchange the x and y columns. Inverse of Relation m x y – 2 – 1 0 – 1 1 – 2 2

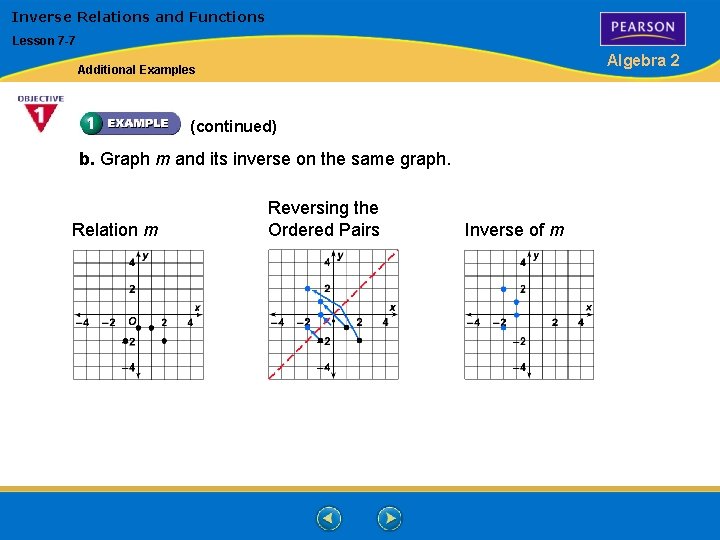
Inverse Relations and Functions Lesson 7 -7 Algebra 2 Additional Examples (continued) b. Graph m and its inverse on the same graph. Relation m Reversing the Ordered Pairs Inverse of m

Inverse Relations and Functions Lesson 7 -7 Algebra 2 Additional Examples Find the inverse of y = x 2 – 2 x = y 2 – 2 ± Interchange x and y. x + 2 = y 2 Solve for y. x+2=y Find the square root of each side.

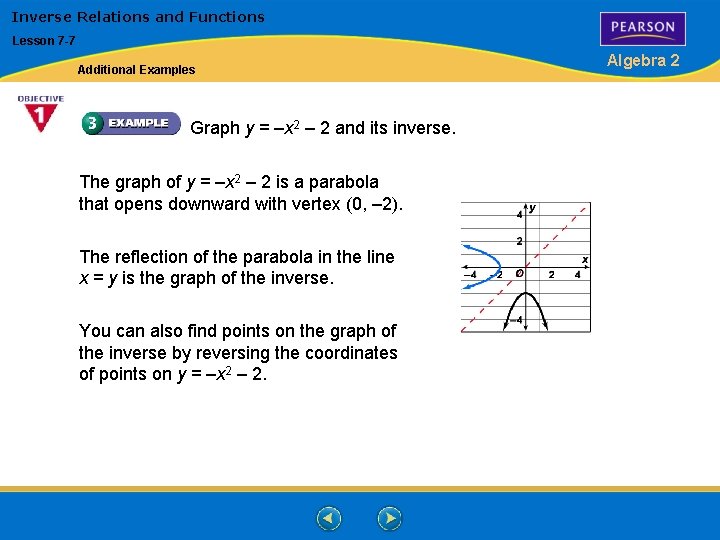
Inverse Relations and Functions Lesson 7 -7 Additional Examples Graph y = –x 2 – 2 and its inverse. The graph of y = –x 2 – 2 is a parabola that opens downward with vertex (0, – 2). The reflection of the parabola in the line x = y is the graph of the inverse. You can also find points on the graph of the inverse by reversing the coordinates of points on y = –x 2 – 2. Algebra 2

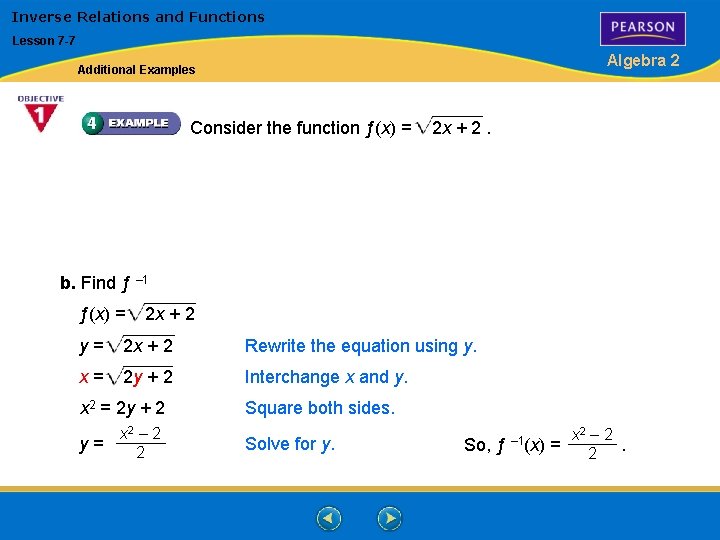
Inverse Relations and Functions Lesson 7 -7 Algebra 2 Additional Examples Consider the function ƒ(x) = 2 x + 2. b. Find ƒ – 1 ƒ(x) = 2 x + 2 y= 2 x + 2 Rewrite the equation using y. x= 2 y + 2 Interchange x and y. x 2 = 2 y + 2 y= x 2 – 2 2 Square both sides. Solve for y. So, ƒ – 1(x) x 2 – 2 = 2.

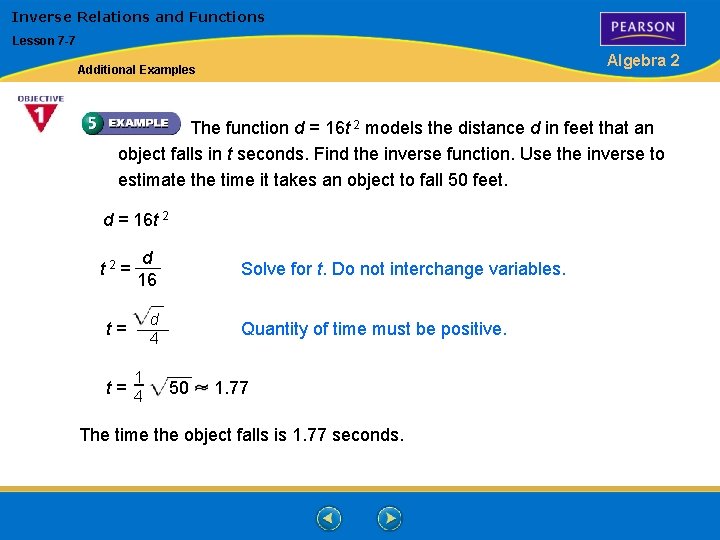
Inverse Relations and Functions Lesson 7 -7 Algebra 2 Additional Examples The function d = 16 t 2 models the distance d in feet that an object falls in t seconds. Find the inverse function. Use the inverse to estimate the time it takes an object to fall 50 feet. d = 16 t 2 = d 16 t= d 4 1 t= 4 Solve for t. Do not interchange variables. Quantity of time must be positive. 50 1. 77 The time the object falls is 1. 77 seconds.

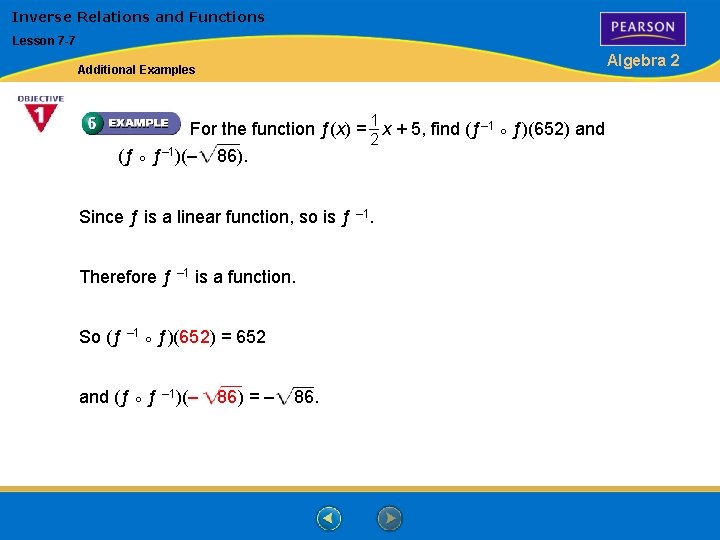
Inverse Relations and Functions Lesson 7 -7 Algebra 2 Additional Examples 1 For the function ƒ(x) = x + 5, find (ƒ– 1 ° ƒ)(652) and 2 – 1 (ƒ ° ƒ )(– 86). Since ƒ is a linear function, so is ƒ – 1. Therefore ƒ – 1 is a function. So (ƒ – 1 ° ƒ)(652) = 652 and (ƒ ° ƒ – 1)(– 86) = – 86.

Algebra 2 Pg 410 3 -33 ev 3 rd