Algebra 2 5 3 Transforming Parabolas Algebra 2

Algebra 2 5 -3 Transforming Parabolas

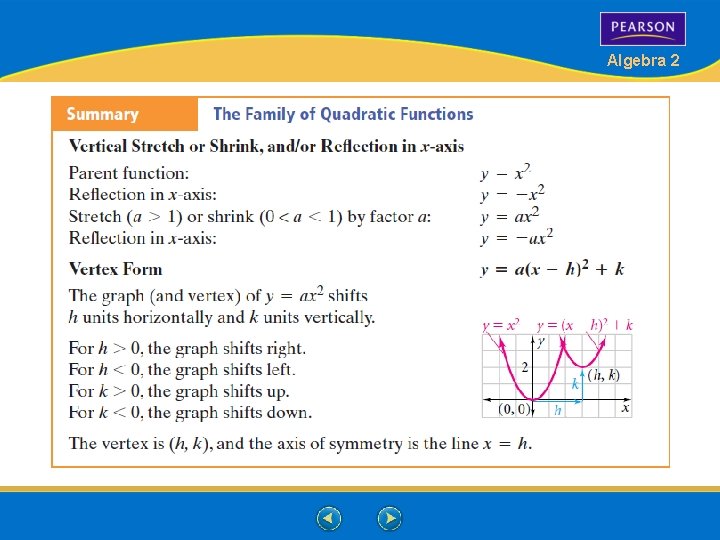
Algebra 2

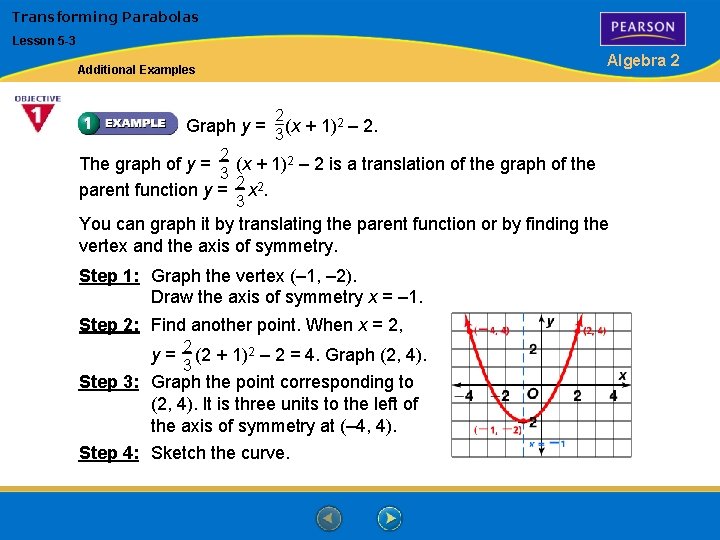
Transforming Parabolas Lesson 5 -3 Algebra 2 Additional Examples 2 Graph y = 3 (x + 1)2 – 2. 2 The graph of y = 3 (x + 1)2 – 2 is a translation of the graph of the parent function y = 2 x 2. 3 You can graph it by translating the parent function or by finding the vertex and the axis of symmetry. Step 1: Graph the vertex (– 1, – 2). Draw the axis of symmetry x = – 1. Step 2: Find another point. When x = 2, y= 2 (2 + 1)2 – 2 = 4. Graph (2, 4). 3 Step 3: Graph the point corresponding to (2, 4). It is three units to the left of the axis of symmetry at (– 4, 4). Step 4: Sketch the curve.

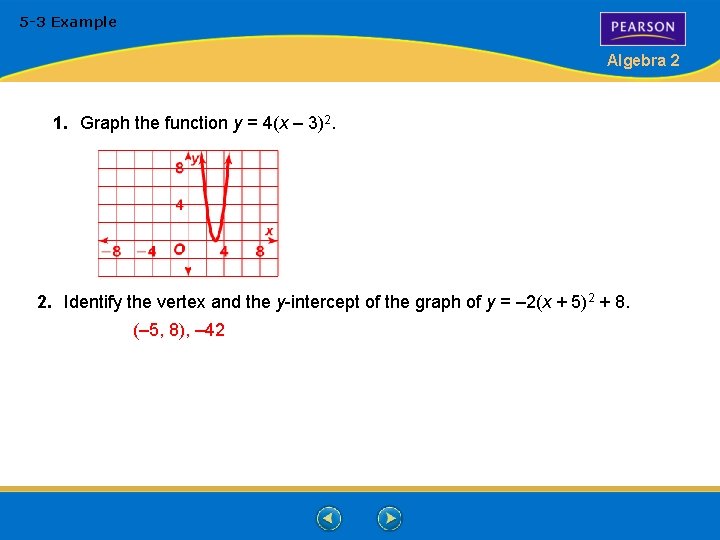
5 -3 Example Algebra 2 1. Graph the function y = 4(x – 3)2. 2. Identify the vertex and the y-intercept of the graph of y = – 2(x + 5)2 + 8. (– 5, 8), – 42

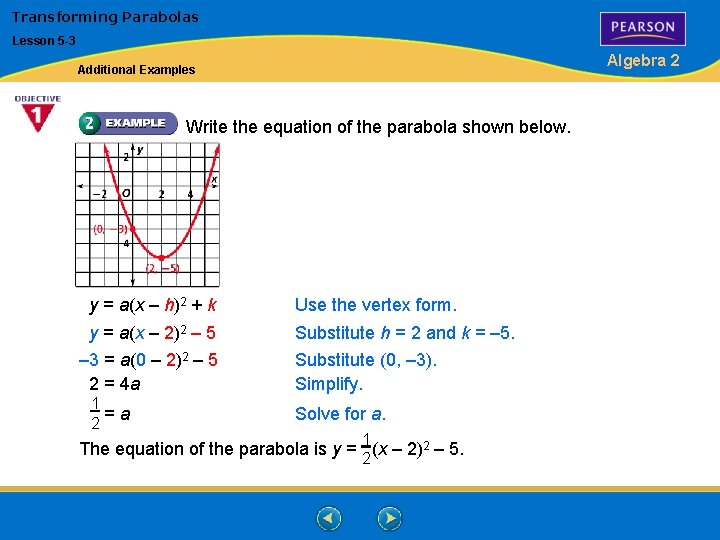
Transforming Parabolas Lesson 5 -3 Algebra 2 Additional Examples Write the equation of the parabola shown below. y = a(x – h)2 + k y = a(x – 2)2 – 5 – 3 = a(0 – 2)2 – 5 2 = 4 a 1 =a 2 Use the vertex form. Substitute h = 2 and k = – 5. Substitute (0, – 3). Simplify. Solve for a. 1 2 The equation of the parabola is y = (x – 2)2 – 5.

Transforming Parabolas Lesson 5 -3 Algebra 2 Additional Examples Write y = – 7 x 2 – 70 x – 169 in vertex form. b 2 a = – (– 70) 2(– 7) x=– Find the x-coordinate of the vertex. Substitute for a and b. = – 5 y = – 7 (– 5)2 – 70(– 5) – 169 Find the y-coordinate of the vertex. =6 The vertex is at (– 5, 6). y = a(x – h)2 + k = – 7(x – (– 5))2 + 6 Write in vertex form. Substitute for a, h and k. = – 7(x + 5)2 + 6 The vertex form of the function is y = – 7(x + 5)2 + 6.

5 -3 Example Algebra 2 3. Write the equation y = 3 x 2 + 12 x – 1 in vertex form. y = 3(x + 2)2 – 13