Algebra 1 Topic 8 Polynomial Operations Table of

Algebra 1 Topic 8 : Polynomial Operations

Table of Contents • Recommended Instructional Design and Planning Continuum ……. Slide 3 • Vocabulary …………………………… Slides 4 – 15 • Pre-Requisite Practice Items ……………………… Slides 16 – 29 • Reporting Category Practice Items ………………… Slides 30 – 41

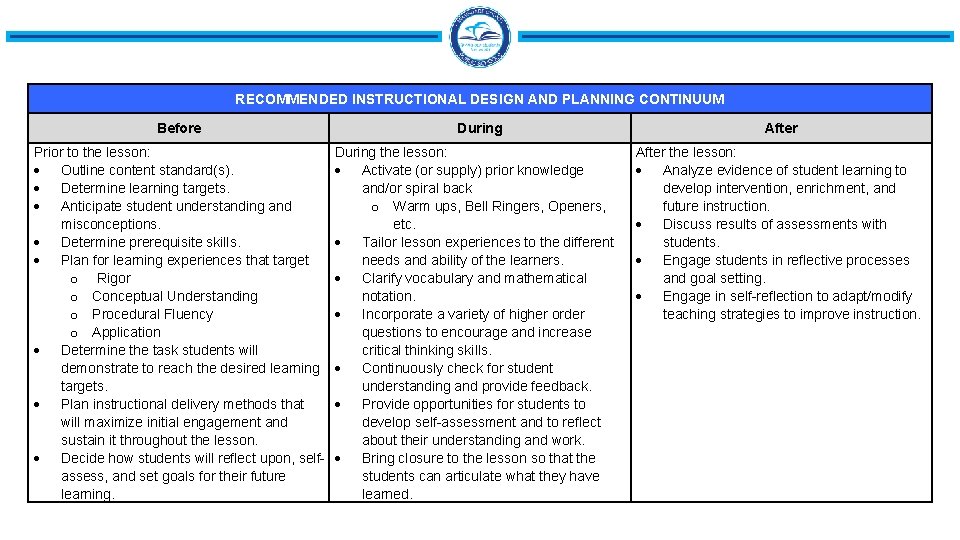
RECOMMENDED INSTRUCTIONAL DESIGN AND PLANNING CONTINUUM Before Prior to the lesson: Outline content standard(s). Determine learning targets. Anticipate student understanding and misconceptions. Determine prerequisite skills. Plan for learning experiences that target o Rigor o Conceptual Understanding o Procedural Fluency o Application Determine the task students will demonstrate to reach the desired learning targets. Plan instructional delivery methods that will maximize initial engagement and sustain it throughout the lesson. Decide how students will reflect upon, selfassess, and set goals for their future learning. During the lesson: Activate (or supply) prior knowledge and/or spiral back o Warm ups, Bell Ringers, Openers, etc. Tailor lesson experiences to the different needs and ability of the learners. Clarify vocabulary and mathematical notation. Incorporate a variety of higher order questions to encourage and increase critical thinking skills. Continuously check for student understanding and provide feedback. Provide opportunities for students to develop self-assessment and to reflect about their understanding and work. Bring closure to the lesson so that the students can articulate what they have learned. After the lesson: Analyze evidence of student learning to develop intervention, enrichment, and future instruction. Discuss results of assessments with students. Engage students in reflective processes and goal setting. Engage in self-reflection to adapt/modify teaching strategies to improve instruction.

Vocabulary

Mathematically Speaking! Choose 3 -4 vocabulary words for the day. Throughout the lesson, as students respond to your questions or are presenting a problem on the board, mark a tally when a vocabulary word is used accurately. This can be turned into a competition among groups or between periods. Examples of accuracy • translation vs slide • variable vs letter • addition property of equality vs adding on both sides

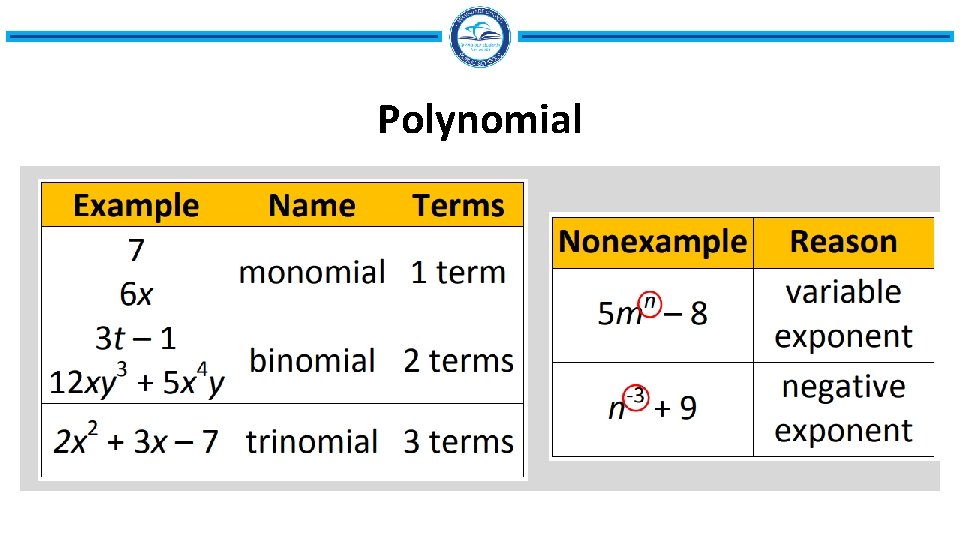
Polynomial

Degree of Polynomial The largest exponent or the largest sum of exponents of a term within a polynomial

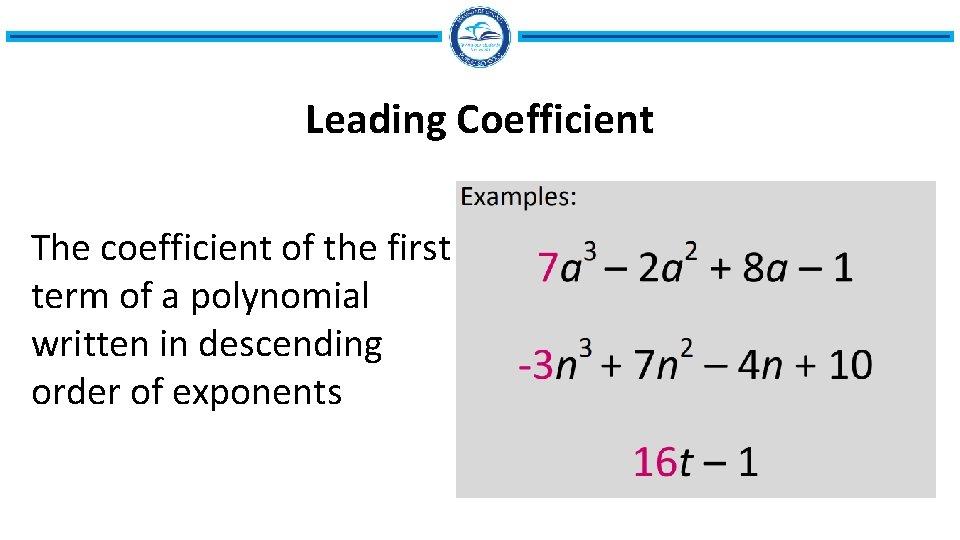
Leading Coefficient The coefficient of the first term of a polynomial written in descending order of exponents

Adding Polynomials Closure property: closed under addition of polynomials

Subtracting Polynomials Closure property: closed under subtraction of polynomials

Multiplying Polynomials Closure property: closed under multiplication of polynomials Apply the distributive property. (a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd Example: (x + 3)(x + 2) = x(x + 2) + 3(x + 2) = x 2 + 2 x + 3 x + 6 = x 2 + 5 x + 6

Multiplying Binomials Apply the distributive property. Example: (x + 8)(2 x – 3) = (x + 8)(2 x + -3) x + 8 2 x + -3 2 x 2 -3 x 16 x -24 2 x 2 + 16 x + -3 x + -24 = 2 x 2 + 13 x – 24

Multiplying Binomials: Squaring a Binomial (a + b)2 = a 2 + 2 ab + b 2 (a – b)2 = a 2 – 2 ab + b 2 Examples: (3 m + n)2 = 9 m 2 + 2(3 m)(n) + n 2 = 9 m 2 + 6 mn + n 2 (y – 5)2 = y 2 – 2(5)(y) + 25 = y 2 – 10 y + 25

Multiplying Binomials: Sum and Difference (a + b)(a – b) = a 2 – b 2 Examples: (2 b + 5)(2 b – 5) = 4 b 2 – 25 (7 – w)(7 + w) = 49 + 7 w – w 2 = 49 – w 2

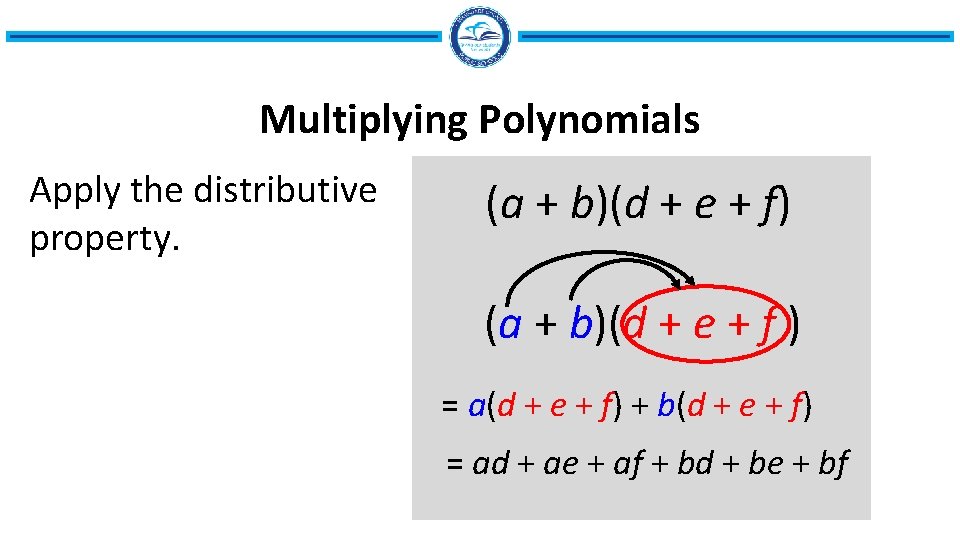
Multiplying Polynomials Apply the distributive property. (a + b)(d + e + f) (a + b)(d + e + f ) = a(d + e + f) + b(d + e + f) = ad + ae + af + bd + be + bf

Pre-Requisite Practice Items

Pre-Requisites MAFS. 6. EE. 1. 3 Watch out for Parenthesis

Pre-Requisites MAFS. 6. EE. 1. 3 Rectangle Perimeter 3

Pre-Requisites MAFS. 6. EE. 1. 3 Generating Equivalent Expressions 1. Lena bought some new clothes for school during tax-free weekend. Jeans cost $35, and shirts cost x dollars. Lena bought three outfits costing her 3(35 + x). Using the Distributive Property, generate an expression equivalent to 3(35 + x). Explain. 2. The area of Mr. Harrison’s rectangular vegetable garden can be represented with the expression 8 x + 16. Using the Distributive Property, rewrite 8 x + 16 as the product of the width (4 meters) and the length. Explain. 4 meters ?

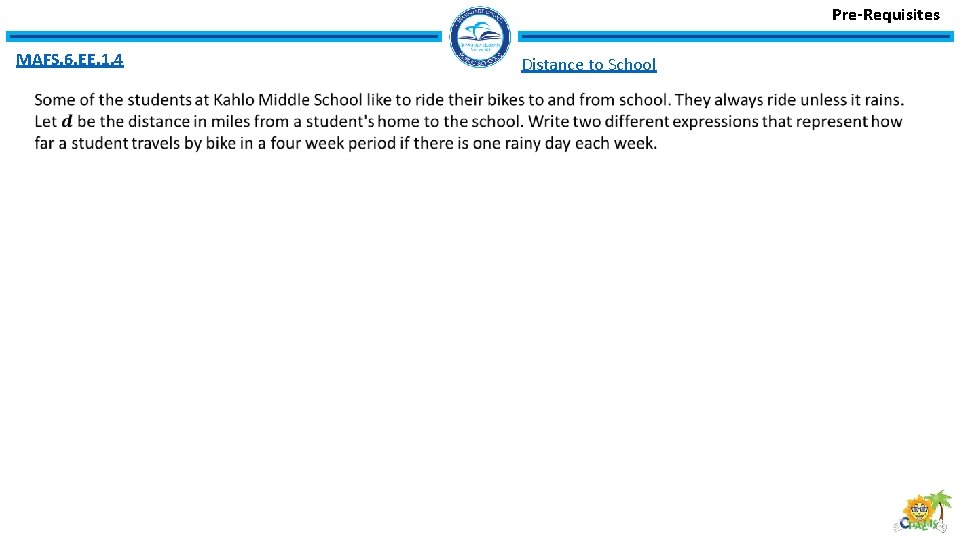
Pre-Requisites MAFS. 6. EE. 1. 4 Distance to School

Pre-Requisites MAFS. 6. EE. 1. 4 Equivalent Expressions

Pre-Requisites MAFS. 6. EE. 1. 4 Rectangle Perimeter 2 Which of the expressions are correct and how might the students have been thinking about finding the perimeter of the rectangle?

Pre-Requisites MAFS. 6. EE. 1. 4 Rectangle Perimeter 3

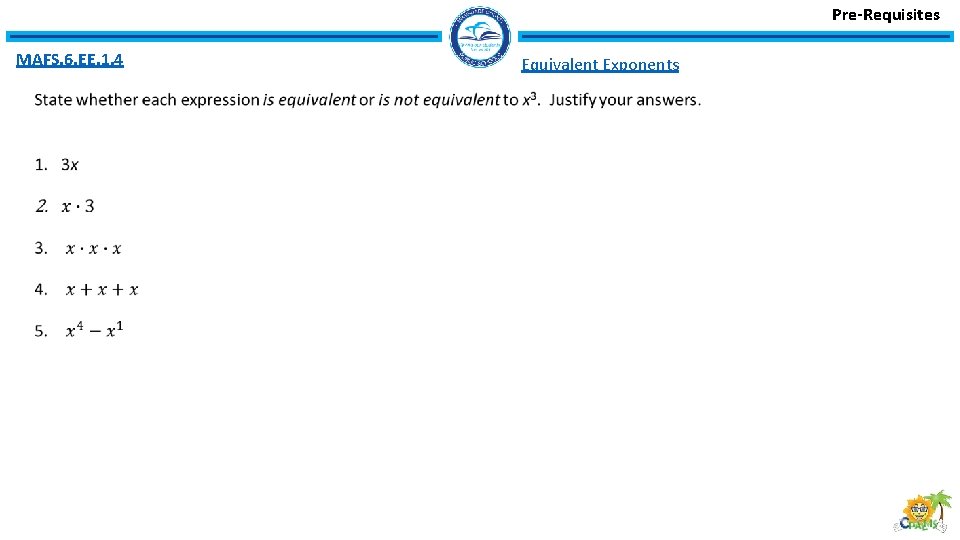
Pre-Requisites MAFS. 6. EE. 1. 4 Equivalent Exponents

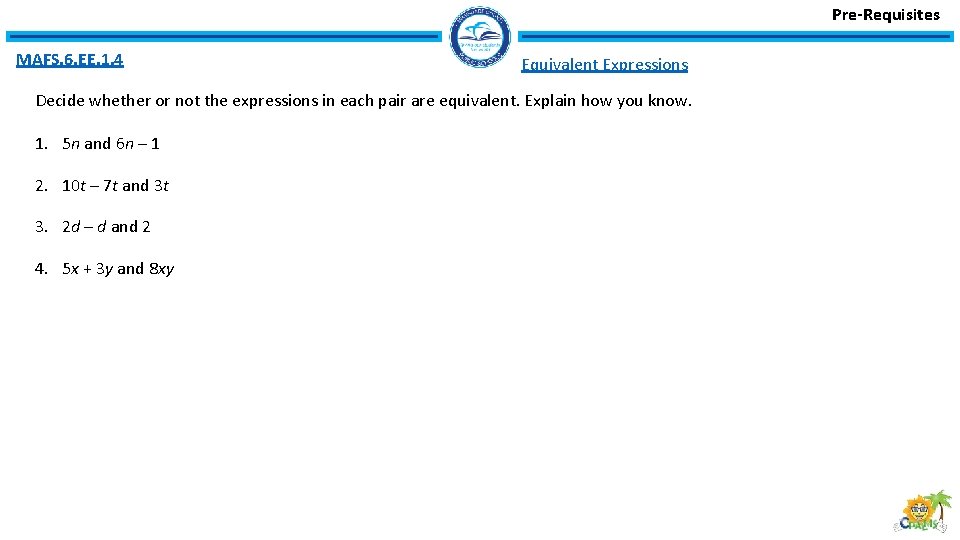
Pre-Requisites MAFS. 6. EE. 1. 4 Equivalent Expressions Decide whether or not the expressions in each pair are equivalent. Explain how you know. 1. 5 n and 6 n – 1 2. 10 t – 7 t and 3 t 3. 2 d – d and 2 4. 5 x + 3 y and 8 xy

Pre-Requisites MAFS. 6. EE. 1. 4 Identifying Equivalent Expressions 6 y + 1 6 y + 7 6(y) + 1(y) 6(y) + 6(1) 6 y + 6

Pre-Requisites MAFS. 6. EE. 1. 4 Property Combinations

Pre-Requisites MAFS. 7. EE. 1. 1 Equivalent Expressions?

Pre-Requisites MAFS. 7. EE. 1. 1 Miles to Kilometers The students in Mr. Sanchez's class are converting distances measured in miles to kilometers. To estimate the number of kilometers, Abby takes the number of miles, doubles it, then subtracts 20% of the result. Renato ﬁrst divides the number of miles by 5, then multiplies the result by 8. a. Write an algebraic expression for each method. b. Use your answer to part (a) to decide if the two methods give the same answer.

Reporting Category Items

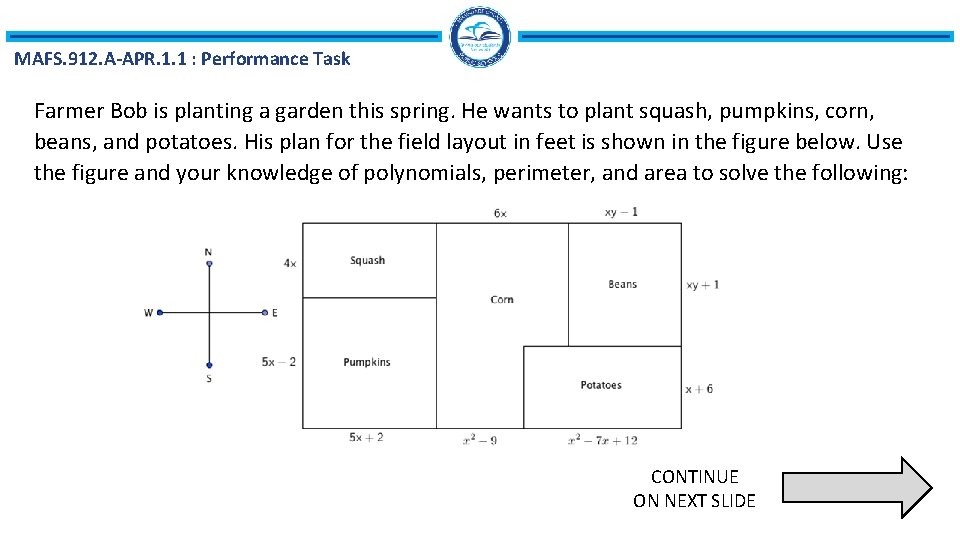
MAFS. 912. A-APR. 1. 1 : Performance Task Farmer Bob is planting a garden this spring. He wants to plant squash, pumpkins, corn, beans, and potatoes. His plan for the field layout in feet is shown in the figure below. Use the figure and your knowledge of polynomials, perimeter, and area to solve the following: CONTINUE ON NEXT SLIDE

MAFS. 912. A-APR. 1. 1 a) Write an expression that represents the length of the south side of the field. b) Simplify the polynomial expression that represents the south side of the field. c) Write a polynomial expression that represents the perimeter of the pumpkin field. d) Simplify the polynomial expression that represents the perimeter of the pumpkin field. State one reason why the perimeter would be useful to Farmer Bob. CONTINUE ON NEXT SLIDE

MAFS. 912. A-APR. 1. 1 CONTINUE ON NEXT SLIDE

MAFS. 912. A-APR. 1. 1

MAFS. 912. A-APR. 1. 1 Joey invested $400 and Katie invested $100. Their combined wealth after 5 years is $1160

MAFS. 912. A-APR. 1. 1

MAFS. 912. A-APR. 1. 1 2 a + 2 b + 4

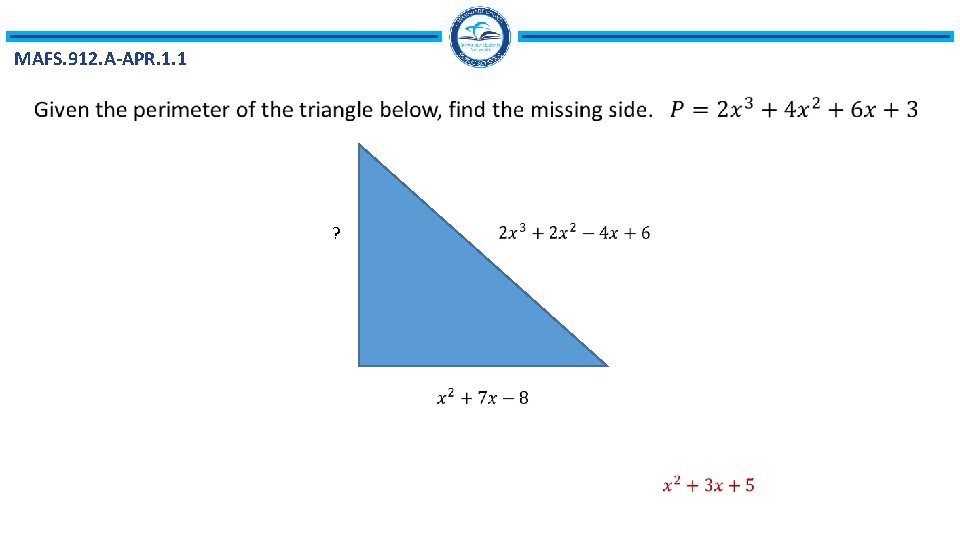
MAFS. 912. A-APR. 1. 1 ?