Algebra 1 Section 8 5 Definition An exponential

Algebra 1 Section 8. 5

Definition An exponential function is a function of the form f(x) = abx, where b > 0 and b ≠ 1.

Example 1 Create a table of ordered pairs for y = 2 x. (-3, ⅛) (-2, ¼) (-1, ½) (0, 1) (1, 2) (2, 4) (3, 8)

Example 1 Create a table of ordered pairs for y = (½)x. (-3, 8) (-2, 4) (-1, 2) (0, 1) (1, ½) (2, ¼) (3, ⅛)

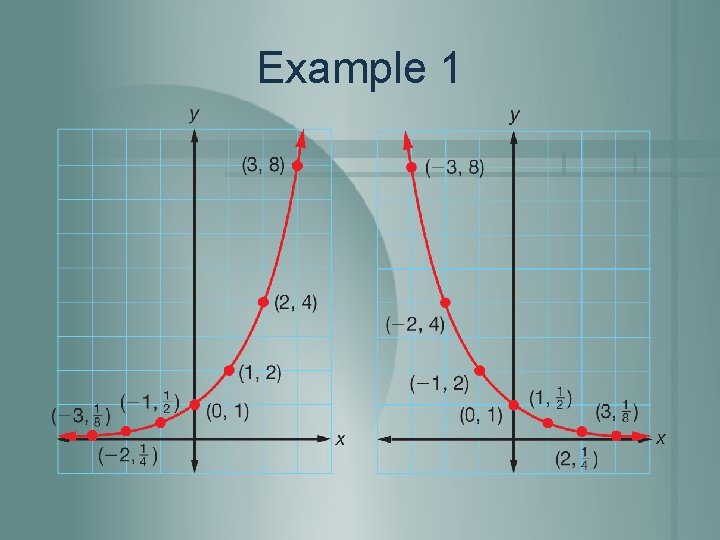
Example 1

Definition An asymptote is a line that a graph approaches but never intersects.

Example 1 In both functions, the domain is the set of all real numbers, and the range is the set of positive real numbers.

Example 2 In this example, we see that the curve of y = a • 2 x differs from y = 2 x in that for every value of x, the corresponding value of y will be a times its previous value. The y-intercept will be (0, a).

Example 3 y = px a) Three consecutive reductions of 75% p = 0. 75; y = 0. 75 x y = 0. 753 ≈ 0. 422 about 42. 2% of the original

Example 3 y = px b) Four consecutive enlargements of 150% p = 1. 5; y = 1. 5 x y = 1. 54 ≈ 5. 063 about 506. 3% of the original

Compound Interest Most real-world investments involve compound interest. Compound interest can be modeled with an exponential function.

Example 4 The total amount is modeled by the equation y = 10, 000(1. 05)n, where n is the number of years. 1 year n=1 y = 10, 000(1. 05)1 = $10, 500

Example 4 The total amount is modeled by the equation y = 10, 000(1. 05)n, where n is the number of years. 2 years n=2 y = 10, 000(1. 05)2 = $11, 025

Example 4 The total amount is modeled by the equation y = 10, 000(1. 05)n, where n is the number of years. 50 years y = 10, 000(1. 05)50 n = 50 ≈ $114, 674 That’s $104, 674 in interest!

Homework: pp. 352 -355