Algebra 1 Section 4 4 Compound Sentences In

Algebra 1 Section 4. 4

Compound Sentences In mathematics, a compound sentence is made by connecting two statements using the word and or the word or.

Definition A conjunction is a compound sentence consisting of mathematical statements connected by the word and.

Conjunctions In order for a conjunction to be true, both parts must be true. The intersection—the values that are in both solutions— forms the solution to the conjunction.

Example 1 Graph the solution set of x > -1 and x ≤ 4.

Example 1 -1 < x ≤ 4 -1 is less than x, which is less than or equal to 4 The symbol is often used for the word and.

Example 2 Graph and state the solution to x ≥ 5 x < 0. Ø: No points in the solution set

Example 3 Solve and graph the solution set of 2 x + 5 ≤ 11 and -3 x > 18. 2 x ≤ 6 x < -6 x≤ 3 x ≤ 3 x < -6

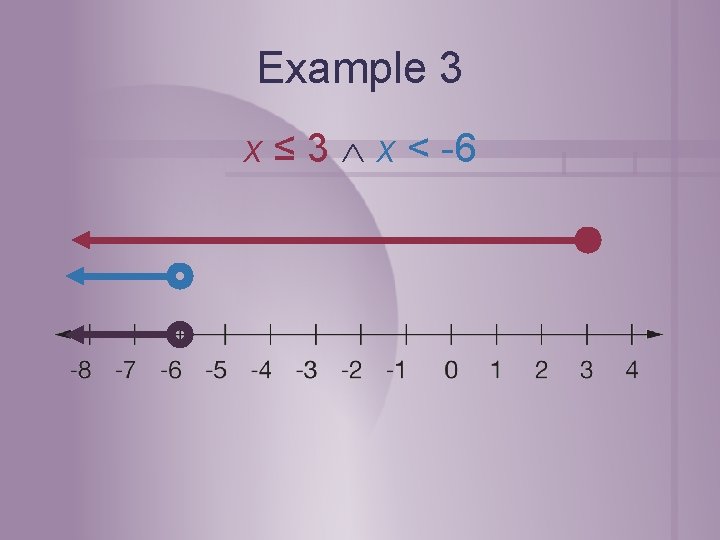
Example 3 x ≤ 3 x < -6

Example 4 The combined conjunction -1 < 3 x + 5 < 8 can be separated into two inequalities separated by the word and: -1 < 3 x + 5 and 3 x + 5 < 8

Example 4 The steps to solve this conjunction can be applied to the combined conjunction, or to the separate inequalities. -1 < 3 x + 5 < 8 -1 < 3 x + 5 and 3 x + 5 < 8

Example 5 In Example 4, both inequalities required the same steps to solve. In Example 5, different steps are required; therefore, the inequalities must be written separately.

Example 5 x – 3 ≤ 2 x – 9 < 15 x – 3 ≤ 2 x – 9 and 2 x – 9 < 15 -3 ≤ x – 9 6≤x x≥ 6 2 x < 24 x < 12

Example 5 x ≥ 6 and x < 12 x ≥ 6 x < 12 6 ≤ x < 12

Example 6 This problem involves a range of values. Brittany’s grade must be at least 80, but less than 90, to get a B in the class. 80 ≤ grade < 90

Example 6 Let t = the score on the 3 rd test 73 + 85 + t 80 ≤ < 90 3 240 ≤ 158 + t < 270 82 ≤ t < 112

Example 6 82 ≤ t < 112 She must get at least an 82. An 82 would get her an average of exactly 80. A grade of 112 is needed for an A; this is not possible.

Homework: pp. 160 -162