Algebra 1 Section 12 2 Solving Quadratic Equations

Algebra 1 Section 12. 2

Solving Quadratic Equations Another method of solving equations of the form x 2 – c = 0 is to isolate the squared term and then take the square root of each side of the equation.

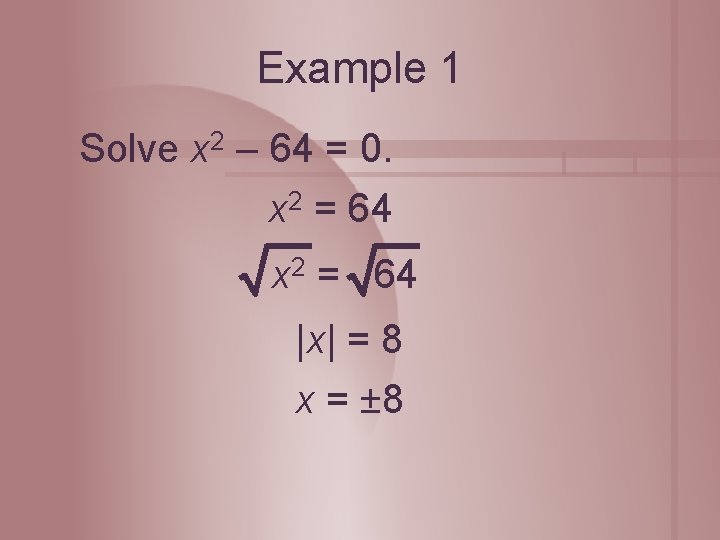
Example 1 Solve x 2 – 64 = 0. x 2 = 64 |x| = 8 x = ± 8

Square Root Property 1. If n ≥ 0 and x 2 = n, then x = ±n. a. If n > 0, then x has two real solutions. b. If n = 0, then x has one real solution.

Square Root Property 2. If n < 0 and x 2 = n, then x has no real solutions.

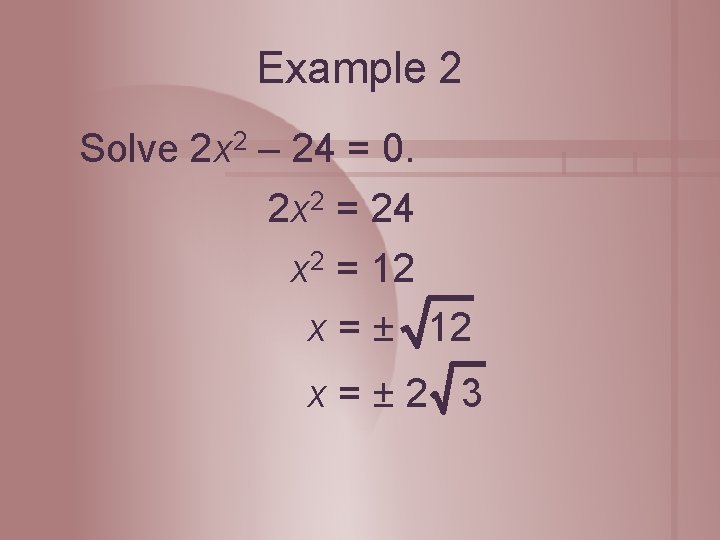
Example 2 Solve 2 x 2 – 24 = 0. 2 x 2 = 24 x 2 = 12 x = ± 12 x=± 2 3

Example 3 Solve (x + 2)2 = 36. x+2=± 6 x = -2 ± 6 x = 4, -8 Did you check each solution in the original equation?

Solving Equations of the Form ax 2 – c = 0 1. Isolate the squared expression. 2. Apply the Square Root Property. 3. Simplify the radical and solve each equation.

Example 4 Solve (x – 5)2 = 21. x – 5 = ± 21 x = 5 ± 21 x ≈ 5 ± 4. 58 The solution set is {0. 42, 9. 58}.

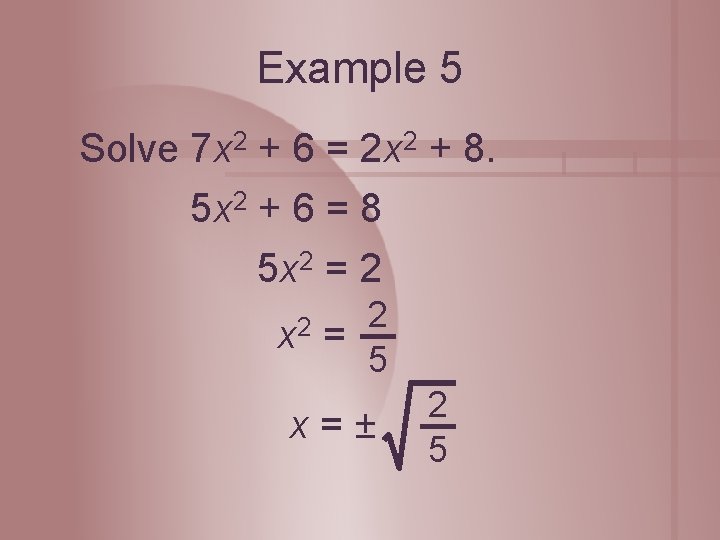
Example 5 Solve 7 x 2 + 6 = 2 x 2 + 8. 5 x 2 + 6 = 8 5 x 2 = 2 x 2 2 = 5 x=± 2 5

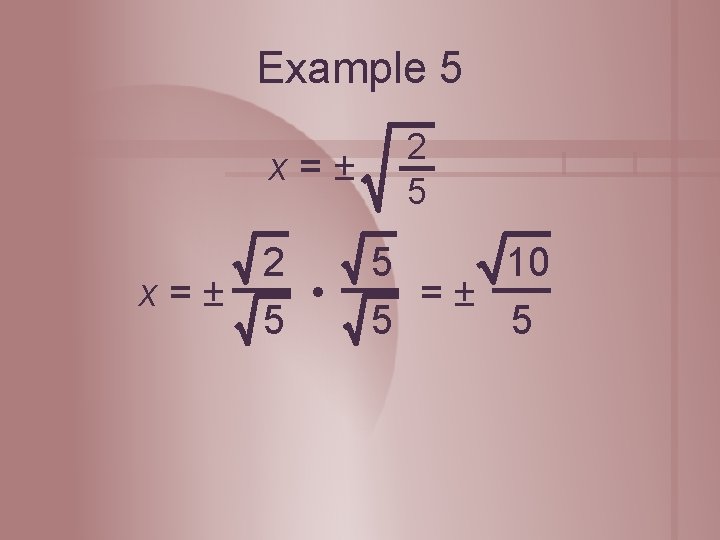
Example 5 x=± 2 x=± • 5 2 5 5 10 =± 5 5

Solving Quadratic Equations Solving x 2 + 7 = 0 yields the solutions x = ± -7. The square root of -7 is not a real number.

Solving Quadratic Equations For now, solve the problem, leaving the negative number under the radical; and state that there are no real solutions.

The Free Fall Equation Assuming negligible air resistance, the height of a dropped object can be modeled by the function h(t) = -16 t 2 + hi, where t is the time in seconds and hi is the initial height in feet.

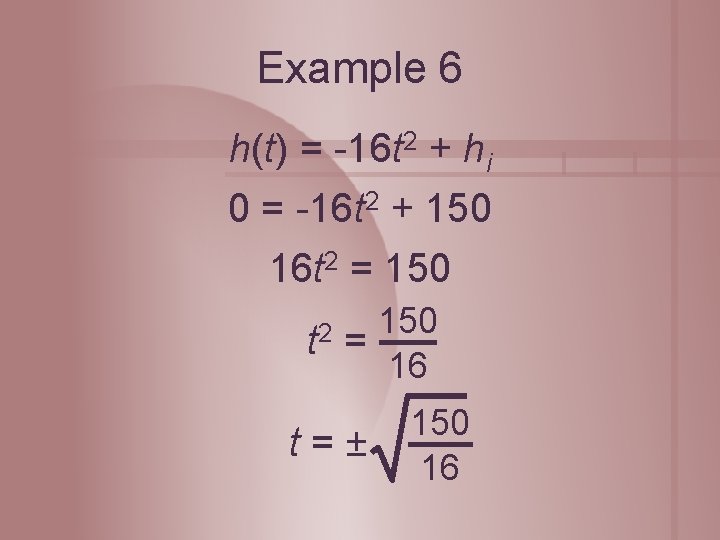
Example 6 h(t) = -16 t 2 + hi 0 = -16 t 2 + 150 16 t 2 = 150 t 2 150 = 16 t=± 150 16

Example 6 t=± 150 16 5 6 t=± ≈ ± 3. 06 4 Only t ≈ 3. 06 sec is a reasonable answer.

Homework: pp. 491 -493