Algebra 1 Section 12 1 Solving Quadratic Equations

Algebra 1 Section 12. 1

Solving Quadratic Equations Linear equations are firstdegree equations, since the variable is only to the first power. Quadratic equations are second-degree equations.

Definition A quadratic equation is an equation of the second degree. Its standard form is ax 2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0.

Zero Product Property In the equation xy = 0, we know that either x = 0 or y = 0, or possibly both equal zero. We use this property to solve quadratic equations. If pq = 0, then p = 0 or q = 0.
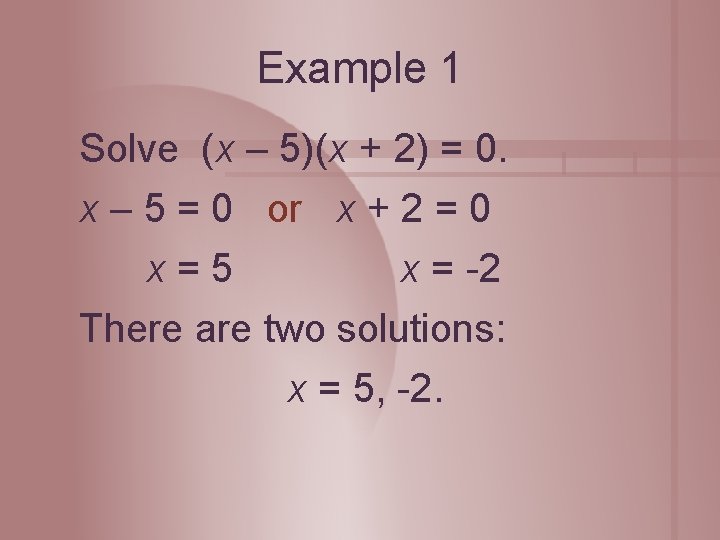
Example 1 Solve (x – 5)(x + 2) = 0. x – 5 = 0 or x + 2 = 0 x=5 x = -2 There are two solutions: x = 5, -2.

Solving Quadratic Equations Many quadratic equations must be factored before you can apply the Zero Product Property. Be sure to have a zero on one side of the equation before factoring.

Example 2 Solve x 2 + 8 x + 12 = 0. (x + 2)(x + 6) = 0 x + 2 = 0 or x + 6 = 0 x = -2 x = -6 Be sure to check your solutions in the original equation.
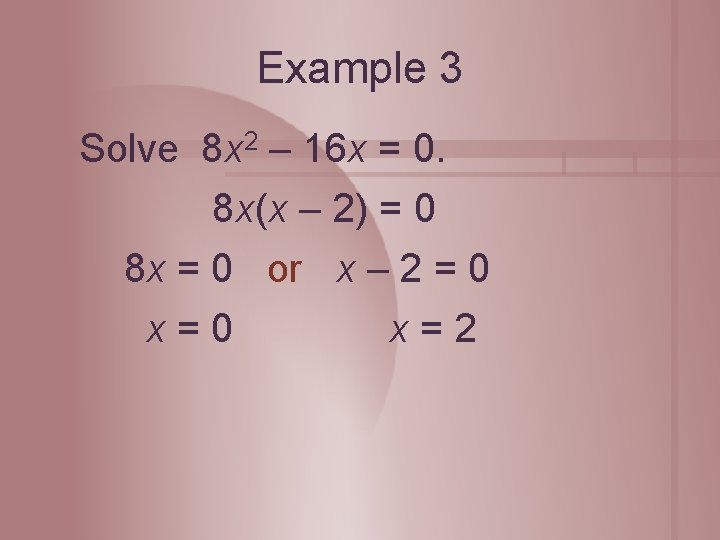
Example 3 Solve 8 x 2 – 16 x = 0. 8 x(x – 2) = 0 8 x = 0 or x – 2 = 0 x=2

Solving Quadratic Equations 1. Write the equation in standard form: ax 2 + bx + c = 0. 2. Factor the polynomial side of the equation. 3. Set each factor that contains a variable equal to zero using the Zero Product Property.

Solving Quadratic Equations 4. Solve the resulting equations. 5. Check your solutions in the original equation.
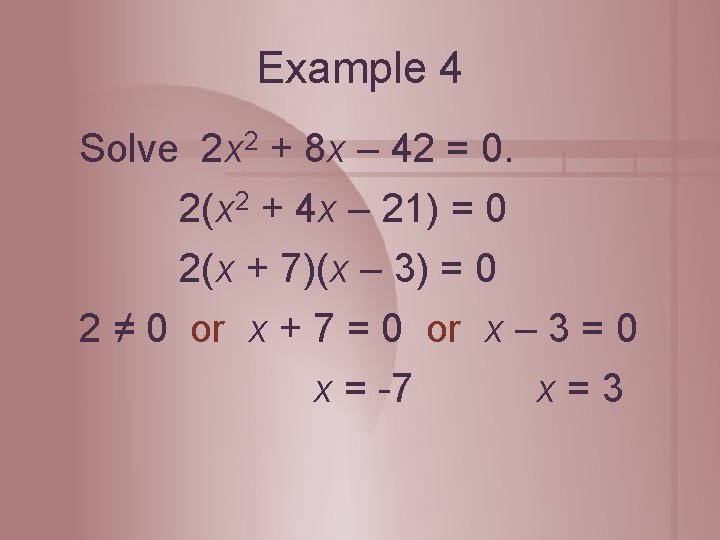
Example 4 Solve 2 x 2 + 8 x – 42 = 0. 2(x 2 + 4 x – 21) = 0 2(x + 7)(x – 3) = 0 2 ≠ 0 or x + 7 = 0 or x – 3 = 0 x = -7 x=3
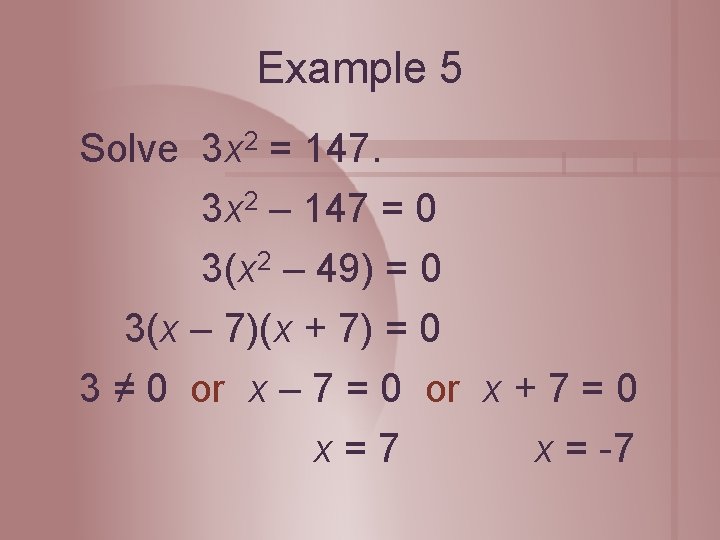
Example 5 Solve 3 x 2 = 147. 3 x 2 – 147 = 0 3(x 2 – 49) = 0 3(x – 7)(x + 7) = 0 3 ≠ 0 or x – 7 = 0 or x + 7 = 0 x=7 x = -7

Solving Quadratic Equations Quadratic equations will have at most two real number solutions. The Zero Product Property can also be applied to equations with higher degrees after they have been factored.

Example 6 Solve 4 x 3 = 14 x 2 + 8 x. 4 x 3 – 14 x 2 – 8 x = 0 2 x(2 x 2 – 7 x – 4) = 0 2 x(2 x + 1)(x – 4) = 0 2 x = 0 or 2 x + 1 = 0 or x – 4 = 0 x=0 x = -½ x=4

Solving Quadratic Equations Dividing both sides of an equation by a variable expression causes a solution to be lost. Some word problems require you to write and solve a quadratic equation.

Example 7 Let w = the width w + 5 = the length Since (length)(width) = area, w(w + 5) = 204 w 2 + 5 w – 204 = 0

Example 7 w 2 + 5 w – 204 = 0 (w + 17)(w – 12) = 0 w + 17 = 0 or w – 12 = 0 w = -17 w = 12 Since the width cannot be negative, w = 12.
![Example 7 The width [w] is 12 ft. The length [w + 5] is Example 7 The width [w] is 12 ft. The length [w + 5] is](http://slidetodoc.com/presentation_image_h2/4b897623e9462948d42c15b7ac9797cb/image-18.jpg)
Example 7 The width [w] is 12 ft. The length [w + 5] is 17 ft. Check: The area is (12 ft)(17 ft) = 204 ft 2.

Homework: pp. 487 -488
- Slides: 19