Algebra 1 Regents Preparation Topic 4 Lets begin

Algebra 1 Regents Preparation Topic 4 Let’s begin by reviewing Pre -Test Item #4. We’ll analyze it using the steps of problem solving, animated on the next slide.

Pre-Test Item 4 (August 2016 #15) Which function has a constant rate of change equal to – 3? (1) x y 0 2 1 5 2 8 3 11 Strategies Question Clues (3) (All of the problem solving prompts will animate here. )

! What (popular) mistakes can we learn from? Which function has a constant rate of change equal to – 3? (1) x y 0 2 1 5 2 8 3 11 +3 Slope is +3, +3 not – 3 +3 Slope is not – 3 (close, but not quite) (3) __ Students y = – 3 x + 5 __ Students

Topic 4: Different representations of linear functions Aim: What concepts and strategies can help you solve Regents problems about this topic? Key Concepts: “y-intercept” is literally the y-value where a graph intercepts the y-axis , which means it’s the y-value when x = 0.

Problem Remixes

How else could the testmakers remix this problem? Which function has a constant rate of change equal to – 3? (1) x y 0 2 1 5 2 8 3 11 +3 Slope is +3, +3 not – 3 Slope is not – 3 (close, but not quite) (3) +3 y = – 3 x + 5

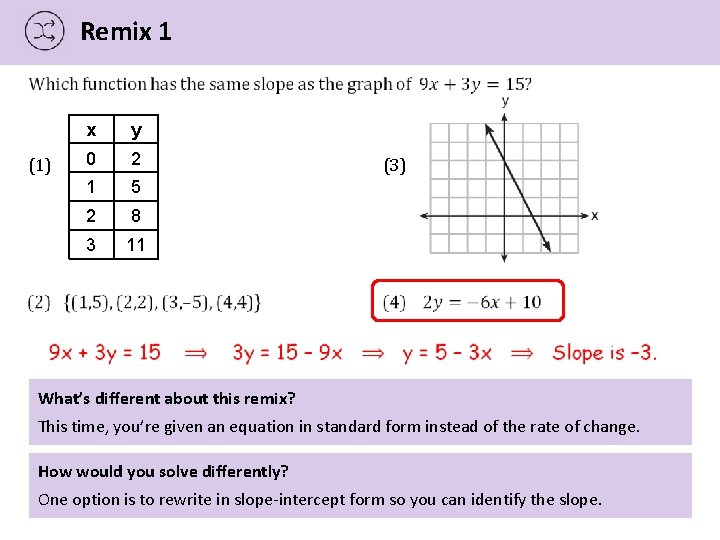
Remix 1 (1) x y 0 2 1 5 2 8 3 11 (3) What’s different about this remix? This time, you’re given an equation in standard form instead of the rate of change. How would you solve differently? One option is to rewrite in slope-intercept form so you can identify the slope.

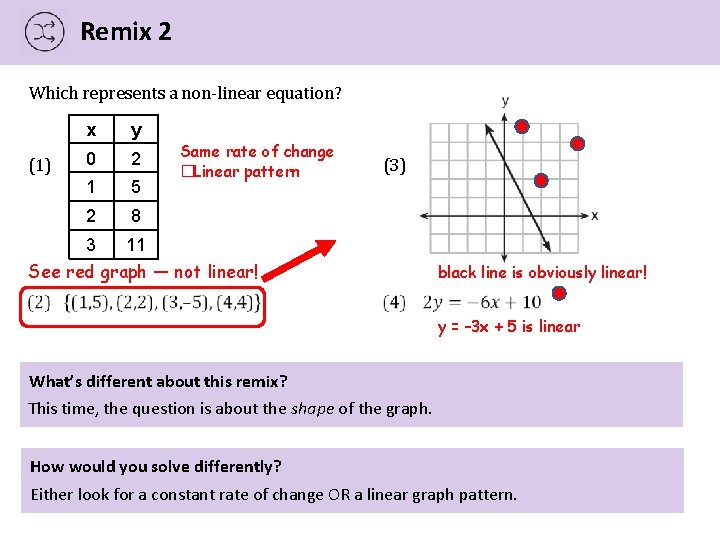
Remix 2 Which represents a non-linear equation? (1) x y 0 2 1 5 2 8 3 11 Same rate of change �Linear pattern (3) See red graph — not linear! black line is obviously linear! y = – 3 x + 5 is linear What’s different about this remix? This time, the question is about the shape of the graph. How would you solve differently? Either look for a constant rate of change OR a linear graph pattern.

Remix 3 Which function has the least y-intercept? (1) x y 0 2 1 5 2 8 3 11 (0, 2) (0, 3) (0, 5) What’s different about this remix? This time, the question asks about y-intercepts; Answer choice 2 is now an equation. How would you solve differently? Look for the y-intercept in each answer choice. Since the y-intercepts the y-axis, that means looking for the y-value where x = 0.

Practice Problems On the practice sheet, work on the problems shown. If you finish early, please do one or more of the following: • Check each other’s solutions. • Make sure you can solve multiple ways — both so that you have options and so that you can check work. • Help classmates. • Post solutions on the board for us to go over. • Work on parts of Lessons 31 -35.

What options do we have for going over solutions and mistakes for the practice problems? 1) Post Solutions on Board 2) Show answers with fingers 3) Post under a Doc Camera Early finishers post solutions on board. Your work be he will re! Write neatl y! I may check 1 or 2 while you work. 4) Post Solutions on Chart Paper and do a Gallery Walk 5) Stand in Four Corners (front) 1 6) Compare to the Solution Slides 2 our classroom 3 4 7) I may collect your papers and give written feedback.

Practice Problem 1: June 2016 #6 All x-jumps = 1. Can look at y-jumps �+7 �+7 consistent �+2 �+4 �+8 inconsistent Also inconsistent

Practice Problem 2: August 2016 #4 Strategy 2: Set Y 1 = – 2 x + 6 and check the calculator table

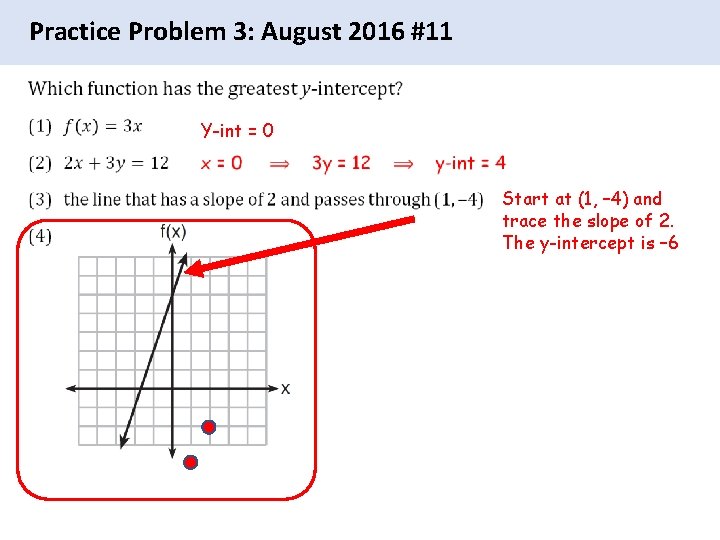
Practice Problem 3: August 2016 #11 Y-int = 0 Start at (1, – 4) and trace the slope of 2. The y-intercept is – 6

Practice Problem 4: June 2015 #11 The graph of a linear equation contains the points (3, 1) and (– 2, 1). Which point also I graphed it. It’s a horizontal line and y always = 1. lies on the graph? (1) (2, 1) (3) (2, 4) (2, 6) (4) (2, 9)

End-of-Lesson Self-Assessment 1) How confident do you now feel with this topic? 2) What do you still need to work on for this topic? (You are welcome to consult a partner. )

Optional Activities

Brain Dump In your notebook or on a separate piece of paper, write down everything you remember learning about: Different Ways You Can Represent a Linear Function You can include: • Definitions • Formulas / “templates” • Graphs or Pictures • Examples • Explanations • How to do Computations

Brain Dump — Sample List Different Ways You Can Represent a Linear Function • Standard Form: Ax + By = C • Slope Intercept Form: y = mx + b • Point-Slope form: y = m(x – h) + k • A table of values has a constant rate of change (∆y/∆x is the same no matter what two points) • You can graph the line given two points. • You can graph the line given a y-intercept and slope. • You can graph the line given a y-intercept and any point.

Math in Motion (Option A) Directions Walk to a place in the room where there is a line with. . . • . . . positive slope. Use two hands to show the line. • . . . 0 slope. Use two hands to show the line. • . . . undefined (infinite) slope. Use two hands to show the line. • negative slope. Use two hands to show the line.

Math in Motion (Option B) Directions Stand at the bottom of a staircase with a partner. • Walk up the staircase exactly with your partner. Partner X measures how far foward you move. Partner B measures how far up. (You can estimate in inches. ) What is the slope of the staircase? • Now, Partner A will walk back down the staircase 1 step at a time. Partner B will walk down 2 steps at a time. Did Partner A walk with a different slope than Person B? Explain why.

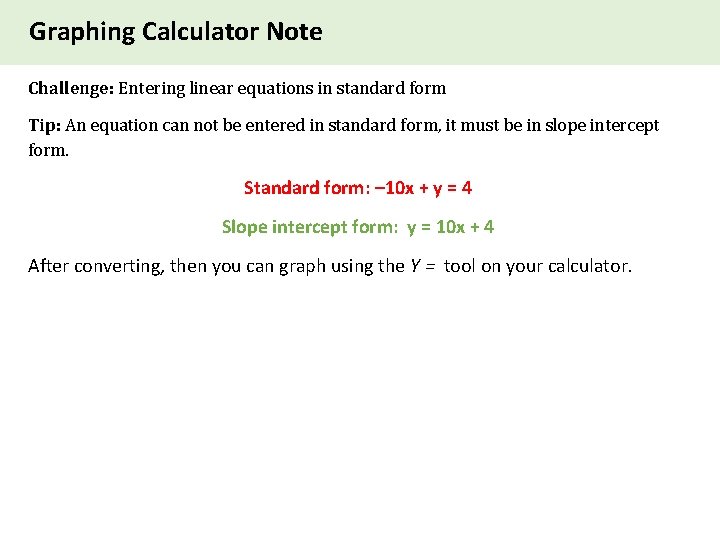
Graphing Calculator Note Challenge: Entering linear equations in standard form Tip: An equation can not be entered in standard form, it must be in slope intercept form. Standard form: – 10 x + y = 4 Slope intercept form: y = 10 x + 4 After converting, then you can graph using the Y = tool on your calculator.

Educators who prepared this lesson Mrs. Asia Goubourn, Catapult Learning Mathematics Coach Mrs. Beth Berg, Catapult Learning Mathematics Coach Editor: Mr. Dennis Desormier, Catapult Learning National Lead Math Consultant The contents of this file are all public domain, including past NYS Regents Exam items, except the text and design at the bottom of slides 2, 3, and 4, which are used with permission by the author.