Algebra 1 Notes Lesson 4 2 Transformations on

Algebra 1 Notes Lesson 4 -2: Transformations on the Coordinate Plane

Mathematics Standards - Number, Number Sense and Operations: Demonstrate fluency in computations using real numbers. - Geometry and Spatial Sense: Identify the reflection and rotation symmetries of two- and three-dimensional geometric figures. - Geometry and Spatial Sense: Perform reflections and rotation using compass and straightedge constructions and dynamic geometry software.

Mathematics Standards - Geometry and Spatial Sense: Derive coordinate rules for translations, reflections and rotations of geometric figures in the coordinate plane. - Geometry and Spatial Sense: Show and describe the results of combinations of translations, reflections and rotations (compositions). - Geometry and Spatial Sense: Analyze twodimensional figures in a coordinate plane.

Vocabulary • Transformation – Movement of figures • Preimage –image before a transformation • Image – Image after a transformation

Reflection A figure is flipped over a line. We will always flip figures over the xaxis or y-axis

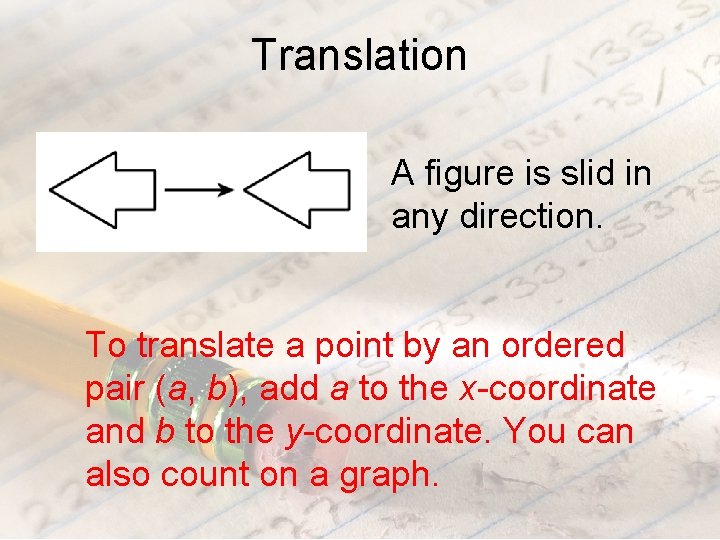
Translation A figure is slid in any direction. To translate a point by an ordered pair (a, b), add a to the x-coordinate and b to the y-coordinate. You can also count on a graph.

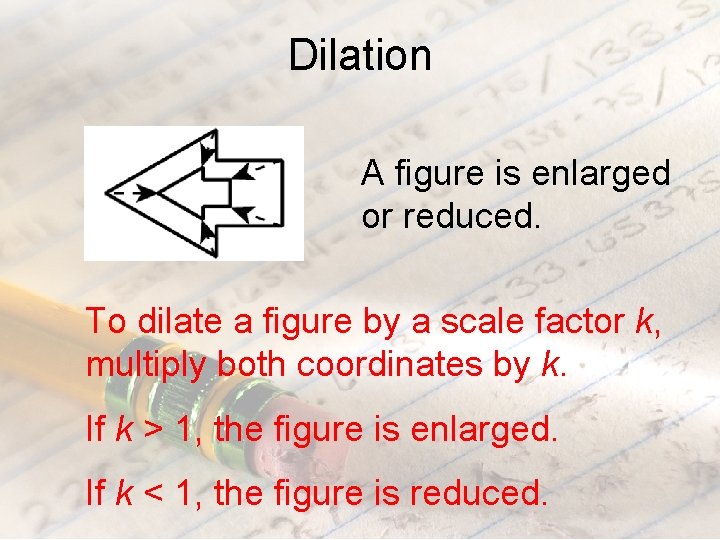
Dilation A figure is enlarged or reduced. To dilate a figure by a scale factor k, multiply both coordinates by k. If k > 1, the figure is enlarged. If k < 1, the figure is reduced.

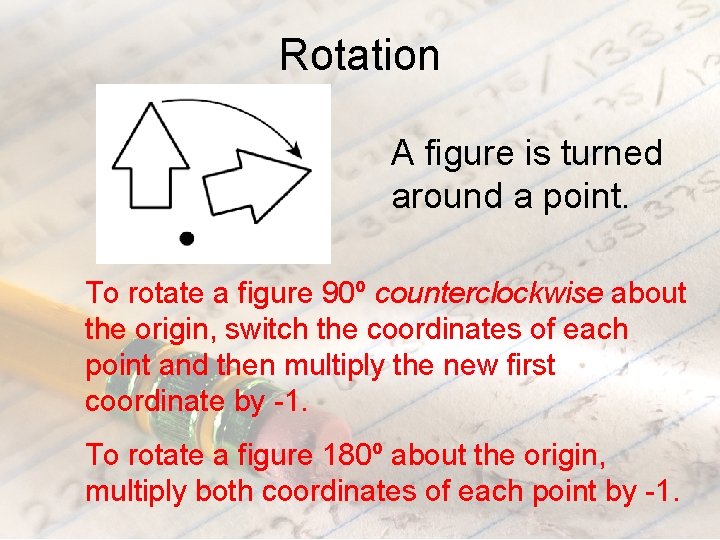
Rotation A figure is turned around a point. To rotate a figure 90º counterclockwise about the origin, switch the coordinates of each point and then multiply the new first coordinate by -1. To rotate a figure 180º about the origin, multiply both coordinates of each point by -1.

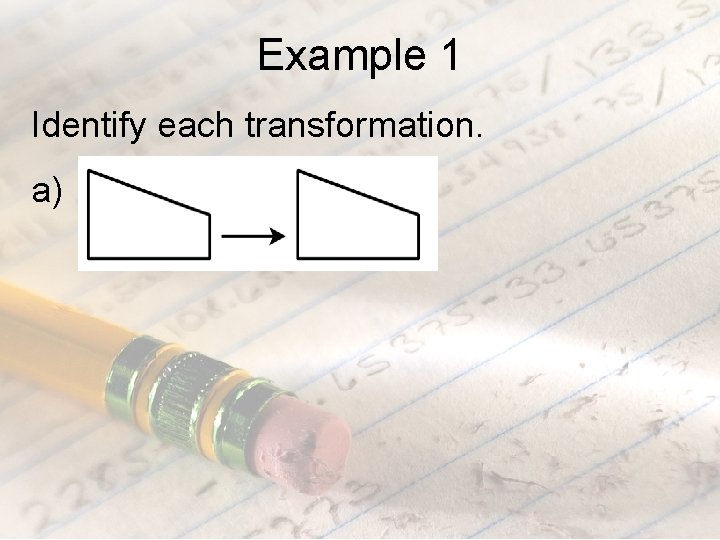
Example 1 Identify each transformation. a)

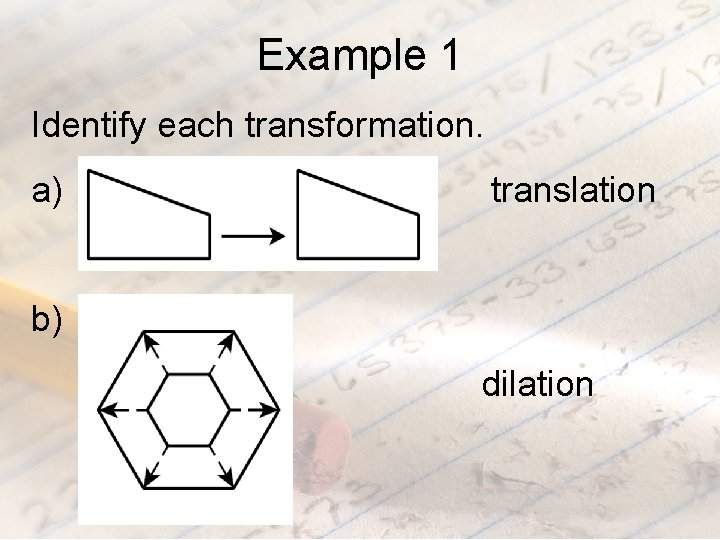
Example 1 Identify each transformation. a) translation b) dilation

Begin Walkthrough