ALGEBRA 1 LESSON 86 7 Function Rules Tables

ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs (For help, go to Lesson 5 -2. ) Graph the data in each table. 1. x – 3 – 1 0 2 y – 7 – 1 2 8 2. x – 3 – 2 0 2 8 -6, 7 y 4 0 – 2 4 3. x – 4 0 2 4 y – 3 – 2 – 1. 5 – 1

ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs Solutions 1. Graph the points: (– 3, – 7) (– 1, – 1) (0, 2) (2, 8) 2. Graph the points: (– 3, 4) (– 2, 0) (0, – 2) (2, 4) 3. Graph the points: (– 4, – 3) (0, – 2) (2, – 1. 5) (4, – 1) 8 -6, 7

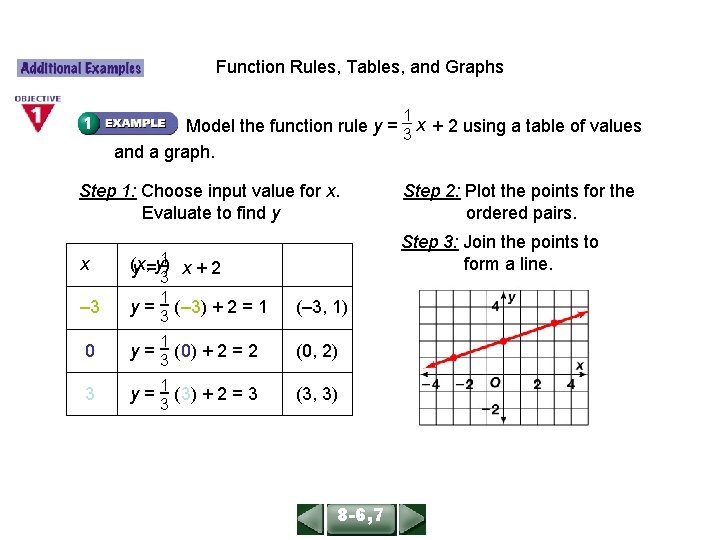
ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs 1 Model the function rule y = 3 x + 2 using a table of values and a graph. Step 1: Choose input value for x. Evaluate to find y Step 3: Join the points to form a line. x 1 (x, y =y) x+2 3 – 3 y = 3 (– 3) + 2 = 1 0 y= 1 (0) + 2 = 2 3 (0, 2) 3 y = 1 (3) + 2 = 3 (3, 3) 1 3 Step 2: Plot the points for the ordered pairs. (– 3, 1) 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs At the local video store you can rent a video game for $3. It costs you $5 a month to operate your video game player. The total monthly cost C(v) depends on the number of video games v you rent. Use the function rule C(v) = 5 + 3 v to make a table of values and a graph. v C(v) = 5 + 3 v (v, C(v)) 0 C(0) = 5 + 3(0) = 5 (0, 5) 1 C(1) = 5 + 3(1) = 8 (1, 8) 2 C(2) = 5 + 3(2) = 11 (2, 11) 8 -6, 7

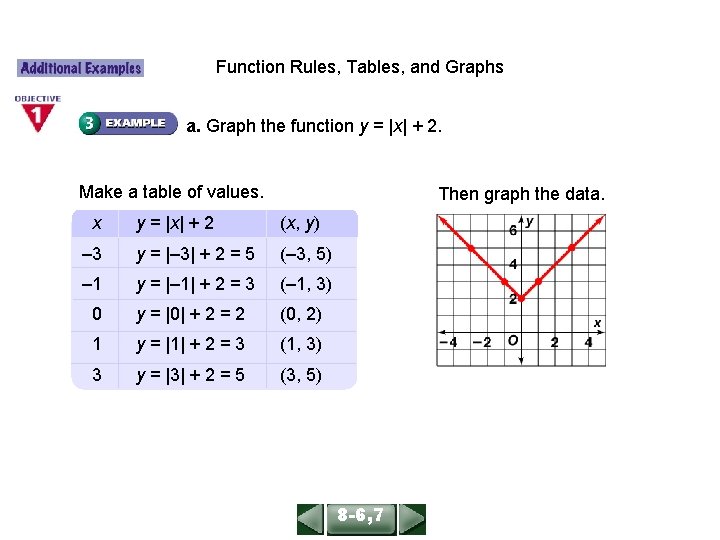
ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs a. Graph the function y = |x| + 2. Make a table of values. x Then graph the data. y = |x| + 2 (x, y) – 3 y = |– 3| + 2 = 5 (– 3, 5) – 1 y = |– 1| + 2 = 3 (– 1, 3) 0 y = |0| + 2 = 2 (0, 2) 1 y = |1| + 2 = 3 (1, 3) 3 y = |3| + 2 = 5 (3, 5) 8 -6, 7

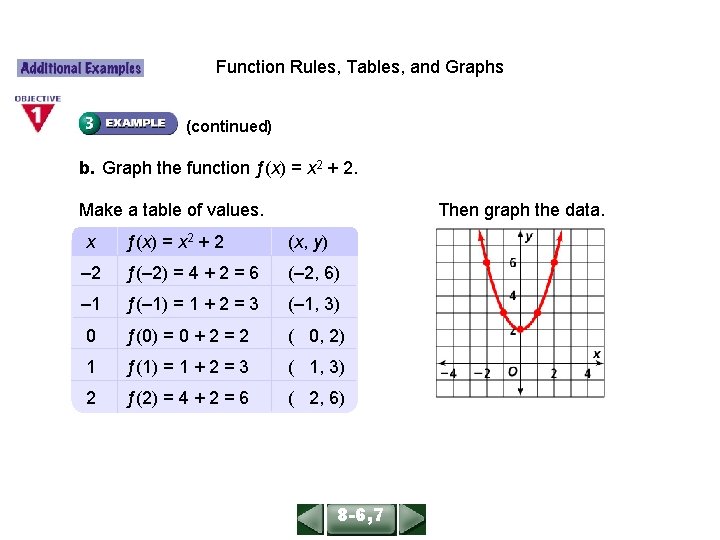
ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs (continued) b. Graph the function ƒ(x) = x 2 + 2. Make a table of values. Then graph the data. x ƒ(x) = x 2 + 2 (x, y) – 2 ƒ(– 2) = 4 + 2 = 6 (– 2, 6) – 1 ƒ(– 1) = 1 + 2 = 3 (– 1, 3) 0 ƒ(0) = 0 + 2 = 2 ( 0, 2) 1 ƒ(1) = 1 + 2 = 3 ( 1, 3) 2 ƒ(2) = 4 + 2 = 6 ( 2, 6) 8 -6, 7

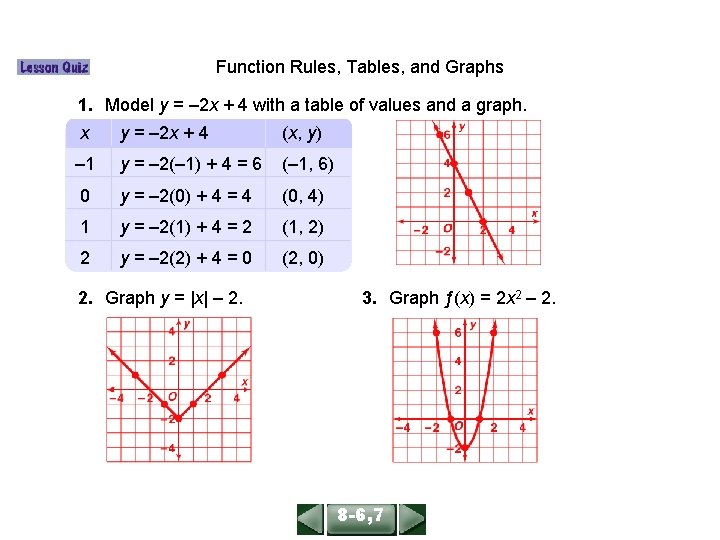
ALGEBRA 1 LESSON 86, 7 Function Rules, Tables, and Graphs 1. Model y = – 2 x + 4 with a table of values and a graph. x y = – 2 x + 4 (x, y) – 1 y = – 2(– 1) + 4 = 6 (– 1, 6) 0 y = – 2(0) + 4 = 4 (0, 4) 1 y = – 2(1) + 4 = 2 (1, 2) 2 y = – 2(2) + 4 = 0 (2, 0) 2. Graph y = |x| – 2. 3. Graph ƒ(x) = 2 x 2 – 2. 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule (For help, go to Lesson 8 -6, 7. ) Model each rule with a table of values. 1. f(x) = 5 x – 1 2. y = – 3 x + 4 3. g(t) = 0. 2 t – 7 4. y = 4 x + 1 5. f(x) = 6 – x 6. c(d) = d + 0. 9 Evaluate each function rule for n = 2. 7. A(n) = 2 n – 1 8. f(n) = – 3 + n – 1 8 -6, 7 9. g(n) = 6 – n

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule Solutions 1. 2. 3. 4. 5. 6. 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule Solutions (continued) 7. A(n) = 2 n – 1 for n = 2: A(2) = 2(2) – 1 = 4 – 1 = 3 8. f(n) = – 3 + n – 1 for n = 2: f(2) = – 3 + 2 – 1 = – 2 9. g(n) = 6 – n for n = 2: g(2) = 6 – 2 = 4 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule Write a function rule for each table. a. x 2 4 6 8 ƒ(x) 8 10 12 14 Ask yourself, “What can I do to 2 to get 8, 4 to get 10, . . . ? ” You add 6 to each x-value to get the ƒ(x) value. Relate: ƒ(x) equals x plus 6 Write: ƒ(x) = x + 6 A rule for the function is ƒ(x) = x + 6. 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule (continued) b. x 1 2 3 4 y 2 5 10 17 Ask yourself, “What can I do to 1 to get 2, 2 to get 5, . . . ? ” You multiply each x-value times itself and add 1 to get the y value. Relate: y Write: y equals x times itself plus = x 2 A rule for the function is y = x 2 + 1. 8 -6, 7 + 1 1

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule The journalism class makes $25 per page of advertising in the yearbook. If the class sells n pages, how much money will it earn? a. Write a function rule to describe this relationship. Relate: money earned is 25 times number of pages sold Define: Let n = number of pages sold. Let P(n) = money earned. Write: P(n) = 25 • n The function rule P(n) = 25 n describes the relationship between the number of pages sold and the money earned. 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule (continued) b. The class sold 6 pages of advertising. How much money did the class make? P(n) = 25 • n P(6) = 25 • 6 Substitute 6 for n. P(6) = 150 Simplify. The class made $150. 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule The choir spent $100 producing audio tapes of its last performance and will sell the tapes for $5. 50 each. Write a rule to describe the choir’s profit as a function of the number of tapes sold. Relate: total profit is $5. 50 times tapes sold minus cost of tape production Define: Let t = number of tapes sold. Let P(t) = total profit. Write: P(t) = 5. 5 t • – 100 The function rule P(t) = 5. 5 t – 100 describes the profit as a function of the number of tapes sold. 8 -6, 7

ALGEBRA 1 LESSON 86, 7 Writing a Function Rule 1. Write a function rule for each table. a. x b. x y – 1 0 1 2 – 5 0 5 10 y = 5 x – 1 0 1 2 ƒ(x) – 4 – 3 – 2 – 1 ƒ(x) = x – 3 2. Write a function rule to describe each relationship. a. the total cost T(c) of c pounds of apples at $. 82 a pound T(c) = 0. 82 c b. a scale model s of a moth m that is 6 times the actual size of the moth s(m) = 6 m 3. You borrow $60 to buy a bread-making machine. You charge customers $1. 50 a loaf for your special bread. Write a rule to describe your profit as a function of the number n of loaves sold. P(n) = 1. 5 n - 60 8 -6, 7