ALGEBRA 1 LESSON 5 2 Relations and Functions

ALGEBRA 1 LESSON 5 -2 Relations and Functions Use the vertical-line test to determine whether the relation {(3, 2), (5, – 1), (– 5, 3), (– 2, 2)} is a function. Step 2: Pass a pencil across the graph. Keep your pencil straight to represent a vertical line. Step 1: Graph the ordered pairs on a coordinate plane. A vertical line would not pass through more than one point, so the relation is a function. 5 -2

ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs (For help, go to Lesson 5 -2. ) Graph the data in each table. 1. x – 3 – 1 0 2 y – 7 – 1 2 8 2. x – 3 – 2 0 2 5 -3 y 4 0 – 2 4 3. x – 4 0 2 4 y – 3 – 2 – 1. 5 – 1

ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs Solutions 1. Graph the points: (– 3, – 7) (– 1, – 1) (0, 2) (0, – 2) (2, 8) (2, 4) 3. 2. (– 3, 4) (– 2, 0) Graph the points: (– 4, – 3) (0, – 2) (2, – 1. 5) (4, – 1) 5 -3

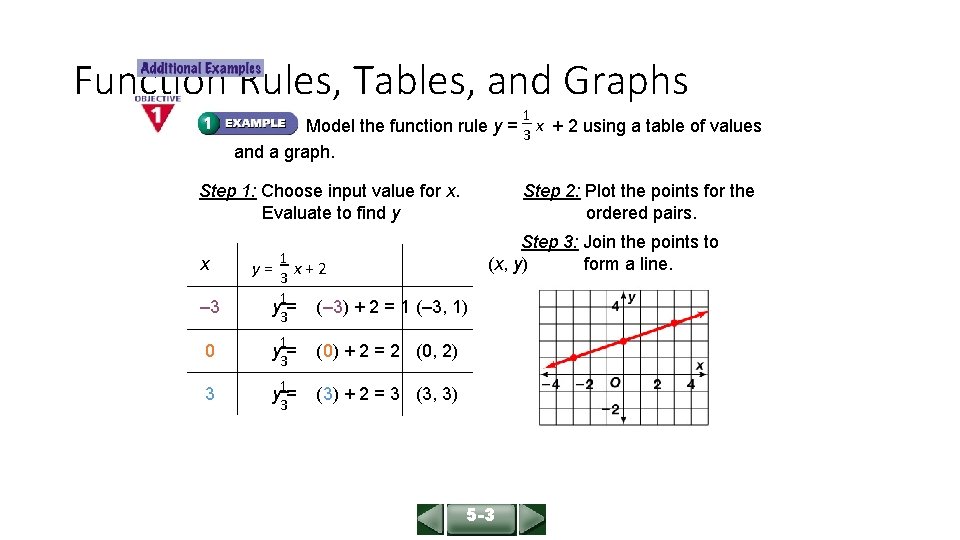
ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs 1 Model the function rule y = 3 x + 2 using a table of values and a graph. Step 1: Choose input value for x. Evaluate to find y x – 3 Step 2: Plot the points for the ordered pairs. 1 y= 3 x+2 1 y 3= (– 3) + 2 = 1 (– 3, 1) 0 y= 1 3 (0) + 2 = 2 (0, 2) 3 y= 1 3 (3) + 2 = 3 (3, 3) Step 3: Join the points to form a line. (x, y) 5 -3

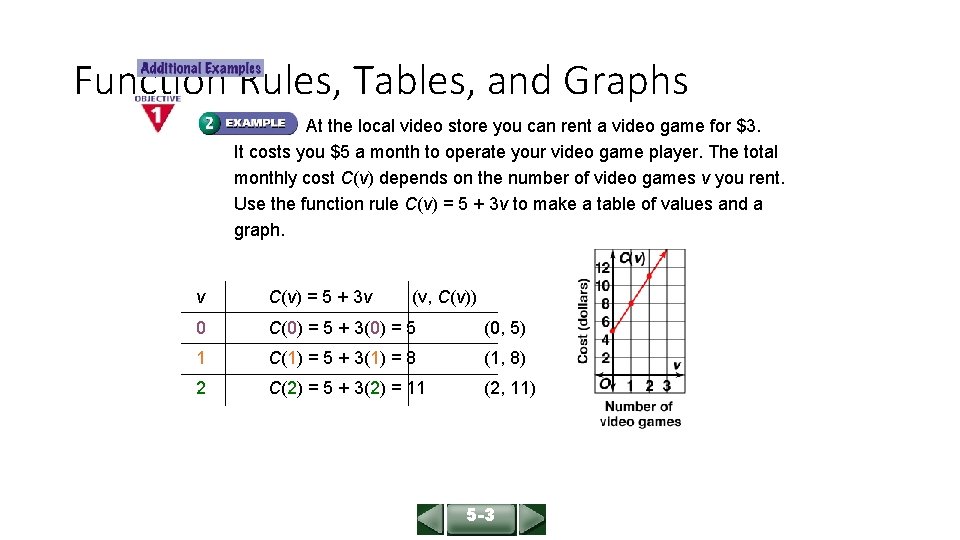
ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs At the local video store you can rent a video game for $3. It costs you $5 a month to operate your video game player. The total monthly cost C(v) depends on the number of video games v you rent. Use the function rule C(v) = 5 + 3 v to make a table of values and a graph. v C(v) = 5 + 3 v (v, C(v)) 0 C(0) = 5 + 3(0) = 5 (0, 5) 1 C(1) = 5 + 3(1) = 8 (1, 8) 2 C(2) = 5 + 3(2) = 11 (2, 11) 5 -3

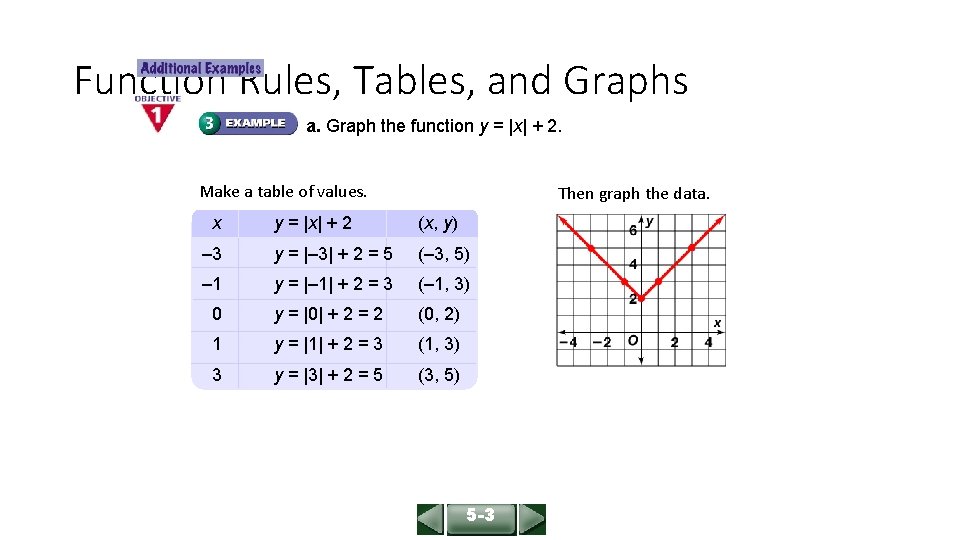
ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs a. Graph the function y = |x| + 2. Make a table of values. x Then graph the data. y = |x| + 2 (x, y) – 3 y = |– 3| + 2 = 5 (– 3, 5) – 1 y = |– 1| + 2 = 3 (– 1, 3) 0 y = |0| + 2 = 2 (0, 2) 1 y = |1| + 2 = 3 (1, 3) 3 y = |3| + 2 = 5 (3, 5) 5 -3

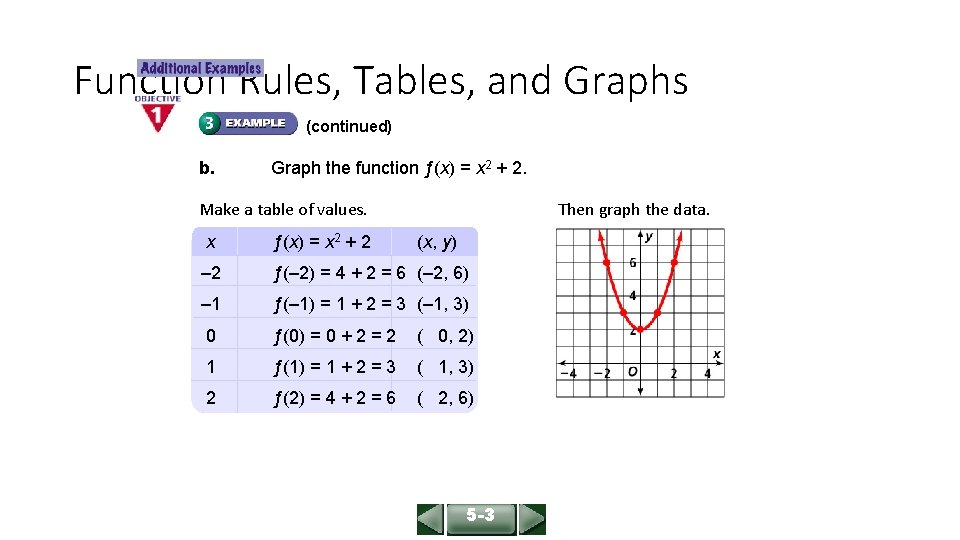
ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs (continued) b. Graph the function ƒ(x) = x 2 + 2. Make a table of values. Then graph the data. x ƒ(x) = x 2 + 2 (x, y) – 2 ƒ(– 2) = 4 + 2 = 6 (– 2, 6) – 1 ƒ(– 1) = 1 + 2 = 3 (– 1, 3) 0 ƒ(0) = 0 + 2 = 2 ( 0, 2) 1 ƒ(1) = 1 + 2 = 3 ( 1, 3) 2 ƒ(2) = 4 + 2 = 6 ( 2, 6) 5 -3

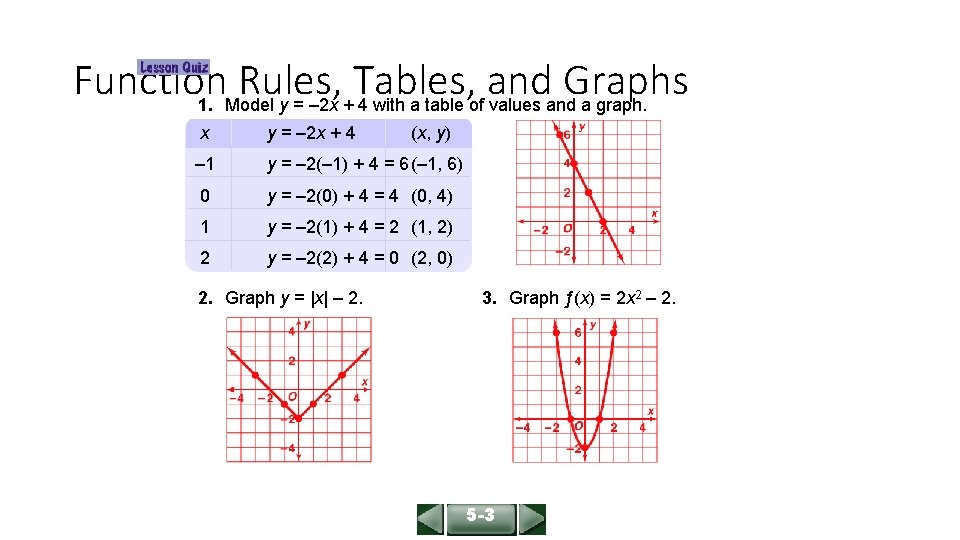
ALGEBRA 1 LESSON 5 -3 Function Rules, Tables, and Graphs 1. Model y = – 2 x + 4 with a table of values and a graph. x y = – 2 x + 4 – 1 y = – 2(– 1) + 4 = 6(– 1, 6) 0 y = – 2(0) + 4 = 4 (0, 4) 1 y = – 2(1) + 4 = 2 (1, 2) 2 y = – 2(2) + 4 = 0 (2, 0) 2. Graph y = |x| – 2. (x, y) 3. Graph ƒ(x) = 2 x 2 – 2. 5 -3

ALGEBRA 1 LESSON 5 -4 Writing a Function Rule (For help, go to Lesson 5 -3. ) Model each rule with a table of values. 1. f(x) = 5 x – 1 2. y = – 3 x + 4 3. g(t) = 0. 2 t – 7 4. y = 4 x + 1 5. f(x) = 6 – x 6. c(d) = d + 0. 9 Evaluate each function rule for n = 2. 7. A(n) = 2 n – 1 8. f(n) = – 3 + n – 1 9. 5 -4 g(n) = 6 – n

ALGEBRA 1 LESSON 5 -4 Writing a Function Rule Solutions 1. 2. 3. 4. 5. 6. 5 -4

ALGEBRA 1 LESSON 5 -4 Writing a Function Rule Solutions (continued) 7. A(n) = 2 n – 1 for n = 2: A(2) = 2(2) – 1 = 4 – 1 = 3 8. f(n) = – 3 + n – 1 for n = 2: f(2) = – 3 + 2 – 1 = – 2 9. g(n) = 6 – n for n = 2: g(2) = 6 – 2 = 4 5 -4