ALGEBRA 1 LESSON 2 3 For help go

ALGEBRA 1 LESSON 2 -3 (For help, go to Lessons 1 -2 and 1 -7. ) Solving Multi-Step Equations Simplify each expression. 1. 2 n – 3 n 2. – 4 + 3 b + 2 + 5 b 3. 9(w – 5) 4. – 10(b – 12) 5. 3(–x + 4) 6. 5(6 – w) Evaluate each expression. 7. 28 – a + 4 a for a = 5 8. 8 + x – 7 x for x = – 3 9. (8 n + 1)3 for n = – 2 10. –(17 + 3 y) for y = 6 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solutions 1. 2 n – 3 n = (2 – 3)n = – 1 n = –n 2. – 4 + 3 b + 2 + 5 b = (3 + 5)b + (– 4 + 2) = 8 b – 2 3. 9(w – 5) = 9 w – 9(5) = 9 w – 45 4. – 10(b – 12) = – 10 b – (– 10)(12) = – 10 b + 120 5. 3(–x + 4) = 3(–x) + 3(4) = – 3 x + 12 6. 5(6 – w) = 5(6) – 5 w = 30 – 5 w 7. 28 – a + 4 a for a = 5: 28 – 5 + 4(5) = 28 – 5 + 20 = 23 + 20 = 43 8. 8 + x – 7 x for x = – 3: 8 + (– 3) – 7(– 3) = 8 + (– 3) + 21 = 5 + 21 = 26 9. (8 n + 1)3 for n = – 2: (8(– 2) + 1)3 = (– 16 + 1)3 = (– 15)3 = – 45 10. –(17 + 3 y) for y = 6: –(17 + 3(6)) = –(17 + 18) = – 35 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solve 3 a + 6 + a = 90 4 a + 6 = 90 Combine like terms. 4 a + 6 – 6 = 90 – 6 Subtract 6 from each side. 4 a = 84 Simplify. 4 a = 84 4 4 Divide each side by 4. a = 21 Simplify. Check: 3 a + 6 + a = 90 3(21) + 6 + 21 90 63 + 6 + 21 90 Substitute 21 for a. 90 = 90 2 -3
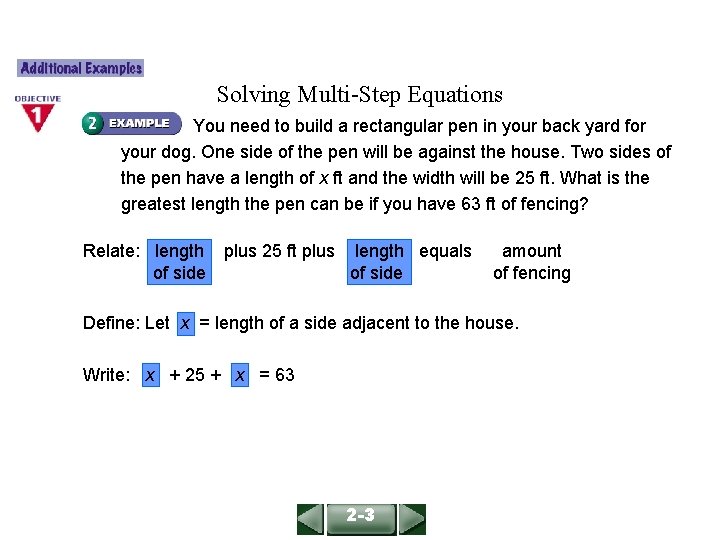
ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations You need to build a rectangular pen in your back yard for your dog. One side of the pen will be against the house. Two sides of the pen have a length of x ft and the width will be 25 ft. What is the greatest length the pen can be if you have 63 ft of fencing? Relate: length of side plus 25 ft plus length equals of side amount of fencing Define: Let x = length of a side adjacent to the house. Write: x + 25 + x = 63 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations (continued) x + 25 + x = 63 2 x + 25 = 63 Combine like terms. 2 x + 25 – 25 = 63 – 25 Subtract 25 from each side. 2 x = 38 Simplify. 2 x = 38 2 2 Divide each side by 2. x = 19 The pen can be 19 ft long. 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solve 2(x – 3) = 8 2 x – 6 = 8 Use the Distributive Property. 2 x – 6 + 6 = 8 + 6 Add 6 to each side. 2 x = 14 Simplify. 2 x = 14 2 2 Divide each side by 2. x = 7 Simplify. 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solve 3 x + x = 17 2 5 Method 1: Finding common denominators 3 x x + 5 = 17 2 3 1 x + x = 17 2 5 15 2 x + x = 17 10 10 Rewrite the equation. 3 1 A common denominator of 2 and 5 is 10. 17 x = 17 10 10 17 10 ( x ) = 17 10 17 (17) Combine like terms. Multiply each by the reciprocal of 17 , which is 10. 10 x = 10 Simplify. 2 -3 17

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solve 3 x + x = 17 2 5 Method 2: Multiplying to clear fractions 3 x x + 5 = 17 2 3 x x 10( 2 + 5 ) = 10(17) 3 x Multiply each side by 10, a common multiple of 2 and 5. x 10( 2 ) + 10( 5 ) = 10(17) 15 x + 2 x = 170 Use the Distributive Property. Multiply. 17 x = 170 Combine like terms. 17 x 170 = 17 17 Divide each side by 17. x = 10 Simplify. 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solve 0. 6 a + 18. 65 = 22. 85. 100(0. 6 a + 18. 65) = 100(22. 85) 100(0. 6 a) + 100(18. 65) = 100(22. 85) 60 a + 1865 = 2285 60 a + 1865 – 1865 = 2285 – 1865 60 a = 420 60 a 420 = 60 60 a = 7 The greatest of decimal places is two places. Multiply each side by 100. Use the Distributive Property. Simplify. Subtract 1865 from each side. Simplify. Divide each side by 60. Simplify. 2 -3

ALGEBRA 1 LESSON 2 -3 Solving Multi-Step Equations Solve each equation. 1. 4 a + 3 – a = 24 7 n 2. – 3(x – 5) = 66 – 17 n 3. 3 + 4 = 7 12 4. 0. 05 x + 24. 65 = 27. 5 57 2 -3

ALGEBRA 1 LESSON 2 -4 (For help, go to Lessons 1 -7 and 2 -3. ) Equations with Variables on Both Sides Simplify. 1. 6 x – 2 x 2. 2 x – 6 x 3. 5 x – 5 x 4. – 5 x + 5 x Solve each equation. 5. 4 x + 3 = – 5 6. –x + 7 = 12 7. 2 t – 8 t + 1 = 43 8. 0 = – 7 n + 4 – 5 n 2 -4

ALGEBRA 1 LESSON 2 -4 Solutions Equations with Variables on Both Sides 1. 6 x – 2 x = (6 – 2)x = 4 x 2. 3. 5 x – 5 x = (5 – 5)x = 0 4. – 5 x + 5 x = (– 5 + 5)x = 0 5. 4 x + 3 = – 5 4 x = – 8 x = – 2 7. 2 t – 8 t + 1 = – 6 t = t= 6. 43 43 42 – 7 8. 2 -4 2 x – 6 x = (2 – 6)x = – 4 x –x + 7 = 12 –x = 5 x = – 5 0 0 12 n n = = – 7 n + 4 – 5 n – 12 n + 4 4 1 3

ALGEBRA 1 LESSON 2 -4 Equations with Variables on Both Sides The measure of an angle is (5 x – 3)°. Its vertical angle has a measure of (2 x + 12)°. Find the value of x. 5 x – 3 = 2 x + 12 Vertical angles are congruent. 5 x – 3 – 2 x = 2 x + 12 – 2 x Subtract 2 x from each side. 3 x – 3 = 12 Combine like terms. 3 x – 3 + 3 = 12 + 3 Add 3 to each side. 3 x = 15 Simplify. 3 x = 15 3 3 Divide each side by 3. x = 5 Simplify. 2 -4

ALGEBRA 1 LESSON 2 -4 Equations with Variables on Both Sides You can buy a skateboard for $60 from a friend and rent the safety equipment for $1. 50 per hour. Or you can rent all items you need for $5. 50 per hour. How many hours must you use a skateboard to justify buying your friend’s skateboard? Relate: cost of plus equipment equals skateboard and equipment friend’s rental skateboard Define: let h = the number of hours you must skateboard Write: 60 + 1. 5 h = 2 -4 5. 5 h

ALGEBRA 1 LESSON 2 -4 Equations with Variables on Both Sides (continued) 60 + 1. 5 h = 5. 5 h 60 + 1. 5 h – 1. 5 h = 5. 5 h – 1. 5 h Subtract 1. 5 h from each side. 60 = 4 h Combine like terms. 60 = 4 h 4 4 Divide each side by 4. 15 = h Simplify. You must use your skateboard for more than 15 hours to justify buying the skateboard. 2 -4

ALGEBRA 1 LESSON 2 -4 Equations with Variables on Both Sides Solve each equation. a. – 6 z + 8 = z + 10 – 7 z – 6 z + 8 = – 6 z + 10 Combine like terms. – 6 z + 8 + 6 z = – 6 z + 10 + 6 z Add 6 z to each side. 8 = 10 Not true for any value of z! This equation has no solution b. 4 – 4 y = – 2(2 y – 2) 4 – 4 y = – 4 y + 4 Use the Distributive Property. 4 – 4 y + 4 y = – 4 y + 4 y Add 4 y to each side. 4 = 4 Always true! The equation is true for every value of y, so the equation is an identity. 2 -4

ALGEBRA 1 LESSON 2 -4 Equations with Variables on Both Sides Solve each equation. 1 1. 3 – 2 t = 7 t + 4 – 9 2. 4 n = 2(n + 1) + 3(n – 1) 1 3. 3(1 – 2 x) = 4 – 6 x no solution 4. You work for a delivery service. With Plan A, you can earn $5 per hour plus $. 75 per delivery. With Plan B, you can earn $7 per hour plus $. 25 per delivery. How many deliveries must you make per hour with Plan A to earn as much as with Plan B? 4 deliveries 2 -4
- Slides: 17