ALevel Maths Core 3 for Edexcel C 3

A-Level Maths: Core 3 for Edexcel C 3. 4 Trigonometry 2 This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 39 © Boardworks Ltd 2006

Contents The addition formulae The double angle formulae Expressions of the form a sin θ + b cos θ Examination-style questions 2 of 39 © Boardworks Ltd 2006

The addition formulae In trigonometry we often have to solve problems involving compound angles. For example, It is important to note that trigonometric functions are not distributive over addition. In other words, In fact, for two angles A and B, This is known as one of the addition formulae (or compound angle formulae) and it should be learnt. 3 of 39 © Boardworks Ltd 2006

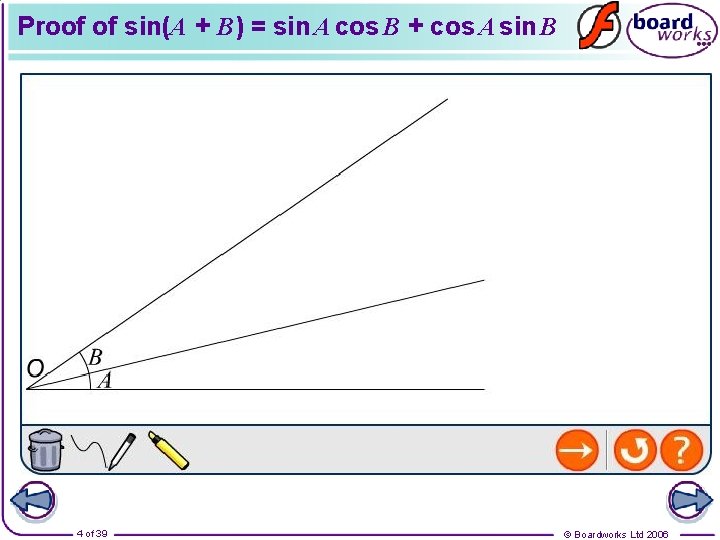
Proof of sin(A + B) = sin A cos B + cos A sin B 4 of 39 © Boardworks Ltd 2006

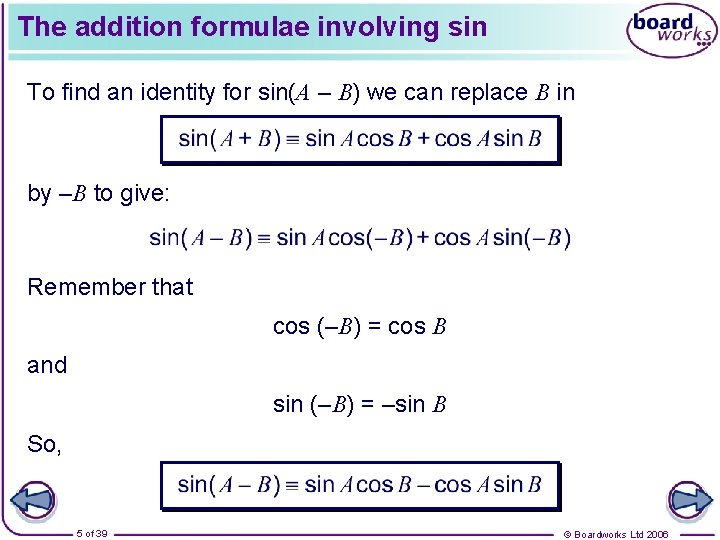
The addition formulae involving sin To find an identity for sin(A – B) we can replace B in by –B to give: Remember that cos (–B) = cos B and sin (–B) = –sin B So, 5 of 39 © Boardworks Ltd 2006

Proof of cos(A + B) = cos A cos B – sin A sin B To find the addition formula for cos(A + B) we can use the fact that cos θ = sin(90 – θ), to give Using the fact that and It follows that the addition formula for cos(A + B) is 6 of 39 © Boardworks Ltd 2006

The addition formulae involving cos To find an identity for cos(A – B) we can replace B in by –B to give: Using the fact that cos (–B) = cos B and sin (–B) = –sin B, we have: 7 of 39 © Boardworks Ltd 2006

The addition formulae involving tan Addition formulae involving tan can be derived from the addition formulae involving sin and cos. Dividing through by cos A cos B gives: 8 of 39 © Boardworks Ltd 2006

The addition formulae involving tan This can be written in terms of tan as: If we replace B by –B we get: 9 of 39 © Boardworks Ltd 2006

Using the addition formulae Use the identity for sin(A + B) to find the exact value of sin 75°. We don’t know the exact value of 75° but we do know the sine and cosine of 30° and 45°. We can write sin 75° as sin (30° + 45°) to give 10 of 39 © Boardworks Ltd 2006

Using the addition formulae Calculate the exact value of Using the identity 11 of 39 © Boardworks Ltd 2006

Using the addition formulae Given that sin A = and cos B = , where A and B are acute, find the exact value of cos (A + B). We can find the value of cos A and sin B using Pythagoras: sin A = So cos A = cos B = 3 1 A ? So sin B = 5 ? 3 B 4 Using these values, 12 of 39 © Boardworks Ltd 2006

Using the addition formulae Solve Using the addition formulae: 13 of 39 © Boardworks Ltd 2006

Using the addition formulae Now, using a calculator, = 52. 5° Tan is positive in the first and third quadrants, so the second solution in the required range is θ = – 180° + 52. 5° S A T C = – 127. 5° So the solution set for – 180° ≤ θ ≤ 180° is – 127. 5° θ = – 127. 5°, 52. 5° 14 of 39 © Boardworks Ltd 2006

Contents The double angle formulae The addition formulae The double angle formulae Expressions of the form a sin θ + b cos θ Examination-style questions 15 of 39 © Boardworks Ltd 2006

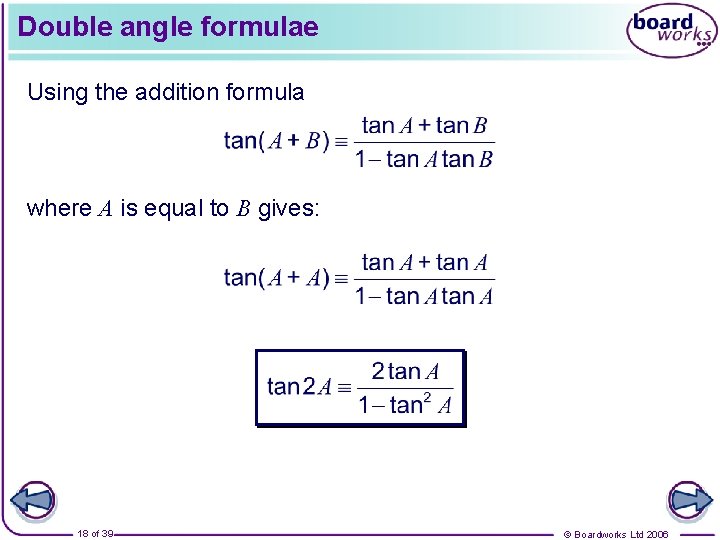
Double angle formulae We can use the addition formulae to derive formulae involving sin 2 A, cos 2 A and tan 2 A. Using the formula where A is equal to B gives: This is the first double angle formula and it should be learnt. 16 of 39 © Boardworks Ltd 2006

Double angle formulae Using the addition formula where A is equal to B gives: We can use the identity sin 2 A + cos 2 A = 1 to write this in two more ways: 17 of 39 © Boardworks Ltd 2006

Double angle formulae Using the addition formula where A is equal to B gives: 18 of 39 © Boardworks Ltd 2006

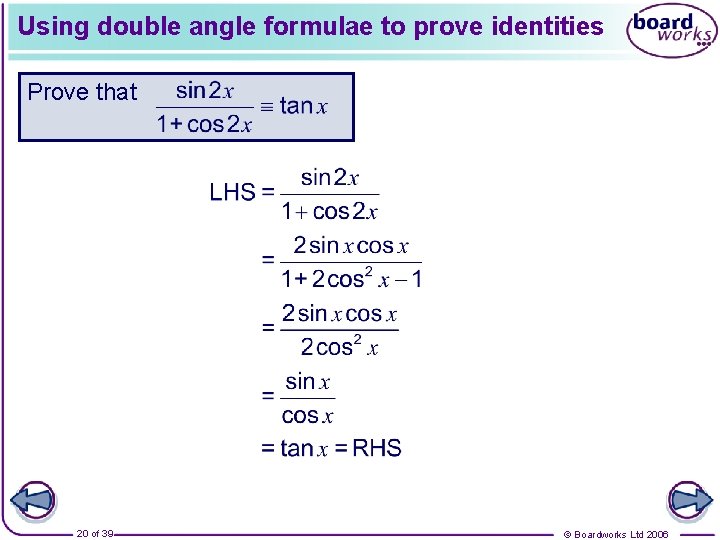
Using double angle formulae to prove identities We can use the double angle formulae to prove other identities involving multiple angles. For example: Use the compound and double angle formulae to prove that 19 of 39 © Boardworks Ltd 2006

Using double angle formulae to prove identities Prove that 20 of 39 © Boardworks Ltd 2006

Solving equations We can also use the double angle formulae to solve equations involving double angles. For example, Solve or θ = 60°, 300° θ = 109. 5°, 250. 5° The complete solution set is θ = 60°, 300°, 109. 5°, 250. 5°. 21 of 39 © Boardworks Ltd 2006

Contents Expressions of the form a sin θ + b cos θ The addition formulae The double angle formulae Expressions of the form a sin θ + b cos θ Examination-style questions 22 of 39 © Boardworks Ltd 2006

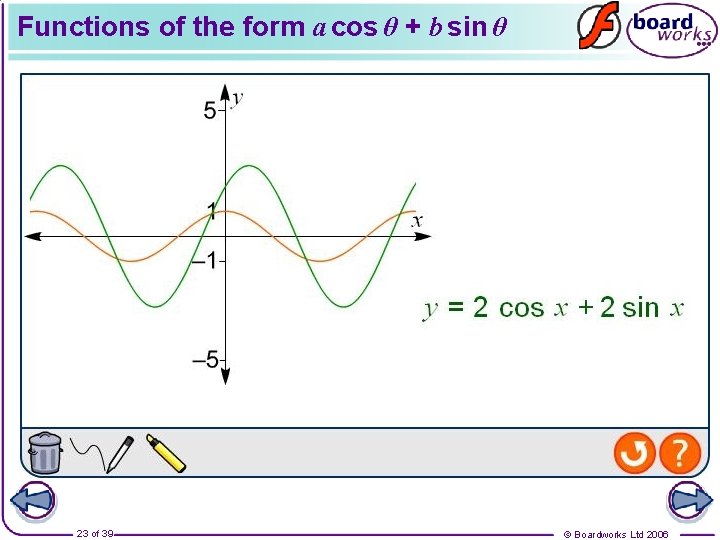
Functions of the form a cos θ + b sin θ 23 of 39 © Boardworks Ltd 2006

Expressions of the form a cos θ + b sin θ As we have seen, the graph of f(θ) = a cos θ + b sin θ can be obtained by stretching a sine or cosine curve vertically and translating it horizontally. Expressions of the form a cos θ + b sin θ can therefore be expressed in the form R cos (θ ± α) or R sin (θ ± α). Suppose we want to express a cos θ + b sin θ in terms of cos only. If we divide and multiply a cos θ + b sin θ by we have 24 of 39 © Boardworks Ltd 2006

Expressions of the form a cos θ + b sin θ Let Now, using a right-angled triangle containing the acute angle α we have: b and α a So 25 of 39 © Boardworks Ltd 2006

Expressions of the form a cos θ + b sin θ But cos α cos θ + sin α sin θ = cos(θ – α), so: = R cos(θ – α) where R = and α = tan– 1. Now use the following right-angled triangle to show that a cos θ + b sin θ can be written in the form R sin(θ + α) where R = and α = tan– 1. b α 26 of 39 a © Boardworks Ltd 2006

Expressions of the form a cos θ + b sin θ In general, for positive values of a, b and R and 0 < α < 90°, it can be shown that: a cos θ + b sin θ = R cos (θ – α) and a cos θ – b sin θ = R cos (θ + α) and a cos θ + b sin θ = R sin (θ + α) and – a cos θ + b sin θ = R sin (θ – α) 27 of 39 © Boardworks Ltd 2006

Equations of the form a cos θ + b sin θ = c Express 3 cos θ + 4 sin θ in the form R cos (θ – α). Start by writing this as an identity: Using the addition formula for cos(A – B) gives: Equating the coefficients of cos θ and sin θ : 28 of 39 © Boardworks Ltd 2006

Equations of the form a cos θ + b sin θ = c Using the following right-angled triangle: R 4 α 3 So, using these values: 3 cos θ + 4 sin θ = 5 cos (θ – 53. 1°) 29 of 39 © Boardworks Ltd 2006

Equations of the form a cos θ + b sin θ = c a) Express 12 sin θ – 5 cos θ in the form R sin(θ – α). b) Solve the equation 12 sin θ – 5 cos θ = 8 in the interval 0 < θ < 360°. a) Using the addition formula for sin(θ – α) gives: Equating the coefficients of cos θ and sin θ : 30 of 39 © Boardworks Ltd 2006

Equations of the form a cos θ + b sin θ = c Using the following right-angled triangle: R 5 α 12 So, using these values 12 sin θ – 5 cos θ = 13 sin (θ – 22. 6°) 31 of 39 © Boardworks Ltd 2006

Equations of the form a cos θ + b sin θ = c b) Using the form found in part a) we can write the equation 12 sin θ – 5 cos θ = 8 as (Using a calculator set to degrees: ) This is the solution in the 2 nd quadrant. So θ – 22. 6° = 38. 0° or 142° θ = 60. 6° or 164. 6° (to 3 s. f. ) 32 of 39 © Boardworks Ltd 2006

Contents Examination-style questions The addition formulae The double angle formulae Expressions of the form a sin θ + b cos θ Examination-style questions 33 of 39 © Boardworks Ltd 2006

Examination-style question 1 The function f is defined by a) Show that when f(x) = 0, . b) Hence solve f(x) = 0 in the interval – 180° < x < 180°. a) 34 of 39 © Boardworks Ltd 2006

Examination-style question 1 b) When f(x) = 0, Dividing through by cos x gives: (Using a calculator set to degrees: ) In the interval – 180° < x < 180°: S – 163. 9° T 35 of 39 A 16. 1° x = 16. 1° or – 164° (to 3 s. f. ) C © Boardworks Ltd 2006

Examination-style question 2 a) Express 2 sin 2θ + 3 cos 2θ in the form R cos (2θ – α), where R > 0 and 0 < α < 90. b) Use the double angle formulae to express 4 sin θ cos θ + 6 cos 2 θ in the form a cos 2θ + b sin 2θ + c where a, b and c are constants to be determined. c) Use your answer to part a) to find the maximum value of 4 sin θ cos θ + 6 cos 2 θ and find the smallest positive value of θ at which it occurs. a) Using the addition formula for cos(2θ – α) gives: 36 of 39 © Boardworks Ltd 2006

Examination-style question 2 Equating the coefficients of cos θ and sin θ : Using the following right-angled triangle: R 2 α 3 So, as required 37 of 39 © Boardworks Ltd 2006

Examination-style question 2 b) We can write as: Using the double angle formulae, we can write this as: c) Using the answer to part a) we can write: 38 of 39 © Boardworks Ltd 2006

Examination-style question 2 Therefore, This reaches its maximum value when Therefore the maximum value of is The smallest positive value of θ at which this maximum occurs is given when 39 of 39 © Boardworks Ltd 2006