ALevel Maths Core 3 for Edexcel C 3

A-Level Maths: Core 3 for Edexcel C 3. 6 Differentiation This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 56 © Boardworks Ltd 2006

The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 2 of 56 © Boardworks Ltd 2006

Review of differentiation So far, we have used differentiation to find the gradients of functions made up of a sum of multiples of powers of x. We found that: and when xn is preceded by a constant multiplier k we have: Also: 3 of 56 © Boardworks Ltd 2006

Review of differentiation We will now look at how to differentiate exponential, logarithmic and trigonometric functions. We will also look at techniques that can be used to differentiate: Compound functions of the form f(g(x)). For example: Products of the form f(x) × g(x), such as: Quotients of the form 4 of 56 , such as: © Boardworks Ltd 2006

The chain rule is used to differentiate composite functions. For instance, suppose we want to differentiate y = (2 x + 1)3 with respect to x. One way to do this is to expand (2 x + 1)3 and differentiate it term by term. Using the binomial theorem: Differentiating with respect to x: 5 of 56 © Boardworks Ltd 2006

The chain rule Another approach is to use the substitution u = 2 x + 1 so that we can write y = (2 x + 1)3 as y = u 3. The chain rule states that: If y is a function of u and u is a function of x, then So if y = u 3 where u = 2 x + 1, Using the chain rule: 6 of 56 © Boardworks Ltd 2006

The chain rule Use the chain rule to differentiate y= with respect to x. Let where u = 3 x 2 – 5 Using the chain rule, 7 of 56 © Boardworks Ltd 2006

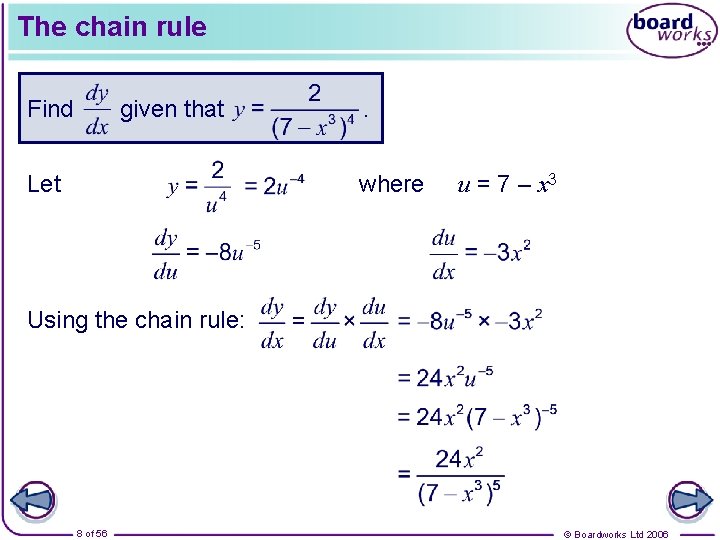
The chain rule Find given that . where Let u = 7 – x 3 Using the chain rule: 8 of 56 © Boardworks Ltd 2006

The chain rule using function notation With practice some of the steps in the chain rule can be done mentally. Suppose we have a composite function y = g(f(x)) If we let y = g(u) then where u = f(x) and Using the chain rule: But u = f(x) so If y = g(f(x)) then 9 of 56 © Boardworks Ltd 2006

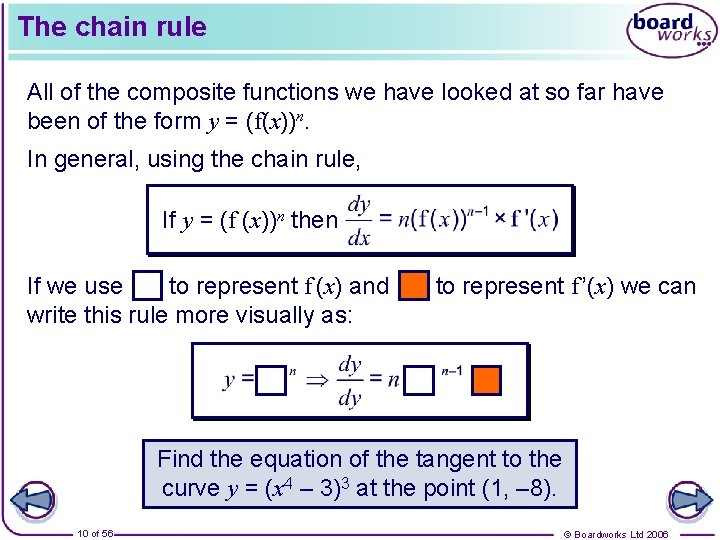
The chain rule All of the composite functions we have looked at so far have been of the form y = (f(x))n. In general, using the chain rule, If y = (f (x))n then If we use to represent f (x) and write this rule more visually as: to represent f ’(x) we can Find the equation of the tangent to the curve y = (x 4 – 3)3 at the point (1, – 8). 10 of 56 © Boardworks Ltd 2006

The chain rule y = (x 4 – 3)3 When x = 1, Using y – y 1 = m(x – x 1) the equation of the tangent at the point (1, – 8) is: y + 8 = 48(x – 1) y = 48 x – 48 – 8 y = 48 x – 56 y = 8(6 x – 7) 11 of 56 © Boardworks Ltd 2006

The relationship between The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 12 of 56 © Boardworks Ltd 2006

The relationship between Suppose we are given x as a function of y instead of y as a function of x. For instance, x = 4 y 2 We can find by differentiating with respect to y: Using the chain rule we can write from which we get: So by the above result, if 13 of 56 8 y then © Boardworks Ltd 2006

The relationship between Find the gradient of the curve with equation x = 2 y 3 – 3 y – 7 at the point (3, 2). x = 2 y 3 – 3 y – 7 At the point (3, 2), y = 2: We can now find the gradient using the fact that 14 of 56 © Boardworks Ltd 2006

Differentiating inverse functions The result is particularly useful for differentiating inverse functions. For example: Find , writing your answer in terms of x. Let y = sin– 1 x so x = sin y Using the identity cos 2 y = 1 – sin 2 y But sin y = x so 15 of 56 © Boardworks Ltd 2006

Differentiating ex and related functions The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 16 of 56 © Boardworks Ltd 2006

The derivative of ex A special property of the exponential function ex is that From this, it follows that where k is a constant. For example, 17 of 56 if y = 4 ex – x 3 © Boardworks Ltd 2006

Functions of the form ekx Suppose we are asked to differentiate a function of the form ekx, where k is a constant. For example, Differentiate y = e 5 x with respect to x. Let where u = 5 x Using the chain rule: In practice, we wouldn’t need to include this much working. 18 of 56 © Boardworks Ltd 2006

Functions of the form ekx We would just remember that in general, For example, We can use the chain rule to extend this to any function of the form ef(x). 19 of 56 © Boardworks Ltd 2006

Functions of the form ef(x) If y = ef(x) then we can let Let where u = f(x) then Using the chain rule: So in general, In words, to differentiate an expression of the form y = ef(x) we multiply it by the derivative of the exponent. 20 of 56 © Boardworks Ltd 2006

Functions of the form ef(x) Using to represent f(x) and to represent f ’(x): For example, 21 of 56 © Boardworks Ltd 2006

Differentiating ln x and related functions The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 22 of 56 © Boardworks Ltd 2006

The derivative of ln x Remember, ln x is the inverse of ex. So, if y = ln x then x = ey Differentiating with respect to y gives: But ey = x so, 23 of 56 © Boardworks Ltd 2006

Functions of the form ln kx Suppose we want to differentiate a function of the form ln kx, where k is a constant. For example: Differentiate y = ln 3 x with respect to x. Let where u = 3 x Using the chain rule: 24 of 56 © Boardworks Ltd 2006

Functions of the form ln kx When functions of the form ln kx are differentiated, the k’s will always cancel out, so in general, We can use the chain rule to extend to functions of the more general form y = ln f(x). Let where u = f(x) then Using the chain rule: 25 of 56 © Boardworks Ltd 2006

Functions of the form ln (f(x)) In general, using the chain rule Using to represent f(x) and to represent f ’(x): For example, 26 of 56 © Boardworks Ltd 2006

Functions of the form ln (f(x)) In some cases we can use the laws of logarithms to simplify a logarithmic function before differentiating it. Remember that, ln (ab) = ln a + ln b Differentiate 27 of 56 ln an = n ln a with respect to x. © Boardworks Ltd 2006

Functions of the form ln (f(x)) ln 2 is a constant and so it disappears when we differentiate. If we had tried to differentiate first, we would have had: without simplifying it The derivative is the same, but the algebra is more difficult. 28 of 56 © Boardworks Ltd 2006

The product rule The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 29 of 56 © Boardworks Ltd 2006

The product rule allows us to differentiate the product of two functions. It states that if y = uv, where u and v are functions of x, then Let u = x 4 and v So 30 of 56 © Boardworks Ltd 2006

The product rule Using the product rule: 31 of 56 © Boardworks Ltd 2006

The product rule Give the coordinates of any stationary points on the curve y = x 2 e 2 x. Let u = x 2 and v So Using the product rule: 32 of 56 © Boardworks Ltd 2006

The product rule When x = 0, y = (0)2 e 0 =0 The point (0, 0) is a stationary point on the curve y = x 2 e 2 x. When x = – 1, y = (– 1)2 e– 2 = e– 2 The point (– 1, e– 2) is also a stationary point on the curve y = x 2 e 2 x. 33 of 56 © Boardworks Ltd 2006

The quotient rule The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 34 of 56 © Boardworks Ltd 2006

The quotient rule allows us to differentiate the quotient of two functions. It states that if y = , where u and v are functions of x, then Find given that Let u = 2 x + 1 . and v = 5 x 2 So 35 of 56 © Boardworks Ltd 2006

The quotient rule 36 of 56 © Boardworks Ltd 2006

The quotient rule Find the equation of the tangent to the curve y = Let at the point (1, 0). u = ln x 4 and v = x 2 So Using the quotient rule: Using ln x 4 = 4 ln x 37 of 56 © Boardworks Ltd 2006

The quotient rule When x = 1, Remember that ln 1 = 0 =4 The gradient of the tangent at the point (1, 0) is 4. Use y – y 1 = m(x – x 1) to find the equation of the tangent at the point (1, 0). y – 0 = 4(x – 1) y = 4 x – 4 38 of 56 © Boardworks Ltd 2006

Differentiating trigonometric functions The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 39 of 56 © Boardworks Ltd 2006

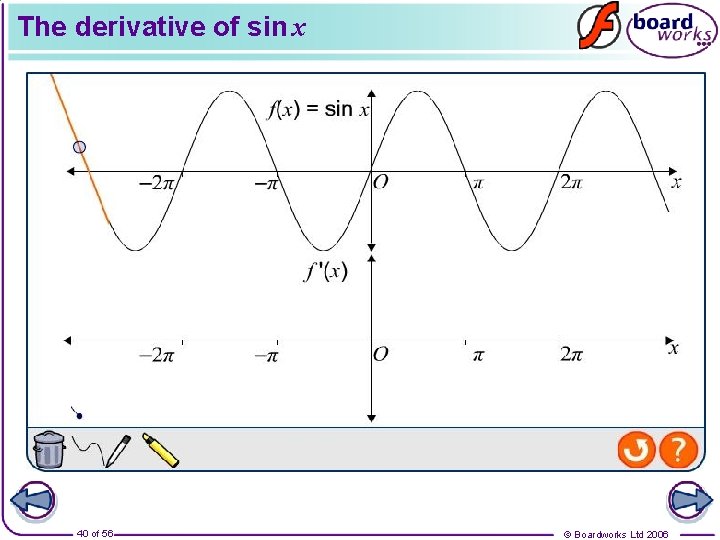
The derivative of sin x 40 of 56 © Boardworks Ltd 2006

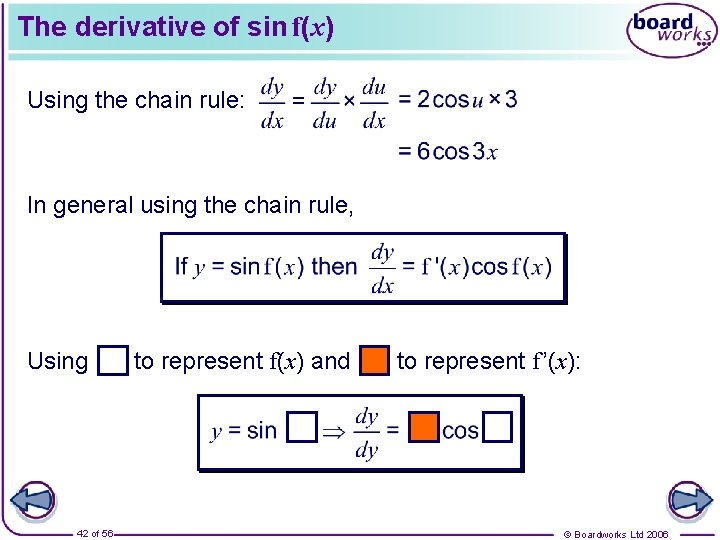
The derivative of sin x By plotting the gradient function of y = sin x, where x is measured in radians, we can deduce that Functions of the form k sin f(x) can be differentiated using the chain rule. Differentiate y = 2 sin 3 x with respect to x. So if y = 2 sin u 41 of 56 where u = 3 x © Boardworks Ltd 2006

The derivative of sin f(x) Using the chain rule: In general using the chain rule, Using 42 of 56 to represent f(x) and to represent f ’(x): © Boardworks Ltd 2006

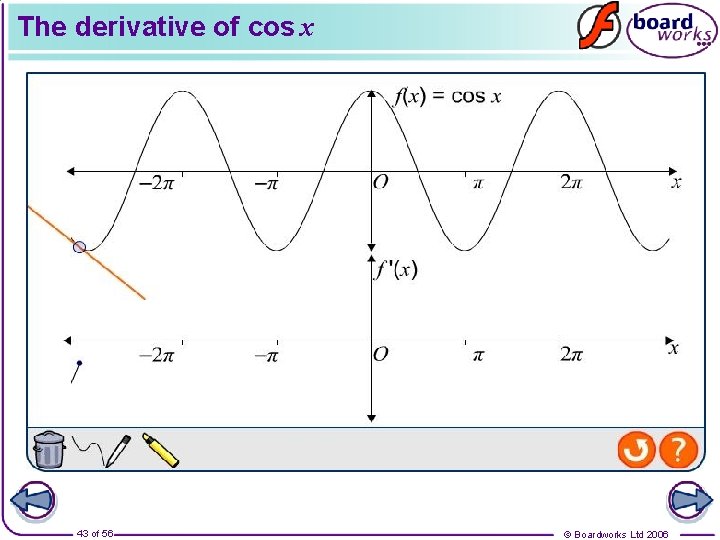
The derivative of cos x 43 of 56 © Boardworks Ltd 2006

The derivative of cos x By plotting the gradient function of y = cos x, where x is measured in radians, we can deduce that Find given that y = –x 2 cos x. Let u = –x 2 and v = cos x So 44 of 56 © Boardworks Ltd 2006

The derivative of cos x Using the product rule: Functions of the form k cos f(x) can be differentiated using the chain rule. Differentiate y = 3 cos (x 3 – 4) with respect to x. So if y = 3 cos u 45 of 56 where u = x 3 – 4 © Boardworks Ltd 2006

The derivative of cos x Using the chain rule: In general using the chain rule, Using 46 of 56 to represent f(x) and to represent f ’(x): © Boardworks Ltd 2006

The derivative of tan x We can differentiate y = tan x (where x is in radians) by writing it as Then we apply the quotient rule with u = sin x and v = cos x : 47 of 56 © Boardworks Ltd 2006

The derivative of sec x We can differentiate y = sec x (where x is in radians) by writing it as Then using the chain rule we get: 48 of 56 © Boardworks Ltd 2006

The derivative of cosec x We can differentiate y = cosec x (where x is in radians) by writing it as Then using the chain rule we get: 49 of 56 © Boardworks Ltd 2006

The derivative of cot x We can differentiate y = cot x (where x is in radians) by writing it as Then we apply the quotient rule with u = cos x and v = sin x: 50 of 56 © Boardworks Ltd 2006

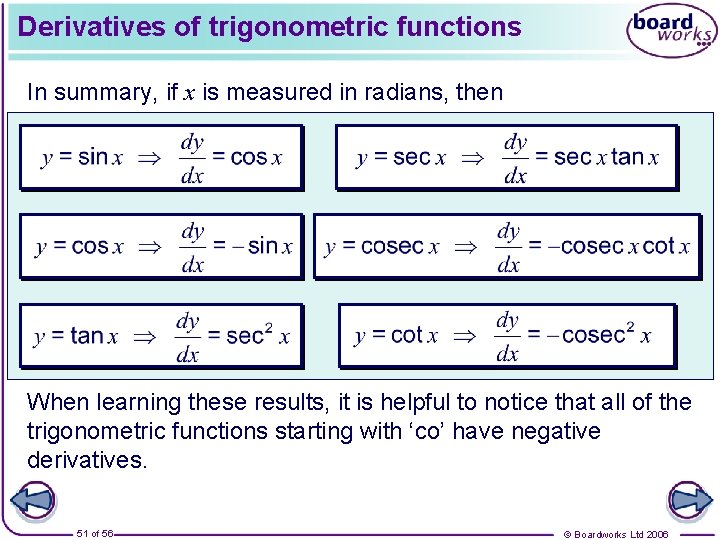
Derivatives of trigonometric functions In summary, if x is measured in radians, then When learning these results, it is helpful to notice that all of the trigonometric functions starting with ‘co’ have negative derivatives. 51 of 56 © Boardworks Ltd 2006

Examination-style question The chain rule Contents The relationship between Differentiating ex and related functions Differentiating ln x and related functions The product rule The quotient rule Differentiating trigonometric functions Examination-style question 52 of 56 © Boardworks Ltd 2006

Examination-style question Given that , a) find f ’(x), b) find the coordinates of any stationary points and determine their nature, c) sketch the curve y = f(x). a) Using the quotient rule: 53 of 56 © Boardworks Ltd 2006

Examination-style question b) When f(x) = 0, When x = 2, When x = – 2, Therefore, the graph of the function points at (2, ) and (– 2, – ). 54 of 56 has turning © Boardworks Ltd 2006

Examination-style question Looking at the gradient just before and just after x = 2: x Value of Slope 1. 9 2 2. 1 0. 01 0 – 0. 01 +ive –ive 0 So (2, ) is a maximum point. Looking at the gradient just before and just after x = – 2: x Value of Slope – 2. 1 – 2 – 1. 9 0. 01 0 – 0. 01 –ive 0 +ive So (– 2, – ) is a minimum point. 55 of 56 © Boardworks Ltd 2006

Examination-style question c) The curve y = 0. crosses the axes when x = 0 and when When x = 0, y = 0. (Also, when y = 0, x = 0). Therefore the curve has one crossing point at the origin, a minimum at (– 2, – ) and a maximum at (2, ): Also, y 0– – 2 0 2 x and, 0+. 56 of 56 © Boardworks Ltd 2006