Alevel Mathematics 2 year Route Map AS Maths

A-level Mathematics - 2 year Route Map AS Maths year 1, A-level Maths year 2 (2017 specification) This route map has been created to provide a suggested route for teaching the A-level Mathematics specification over 2 years. This route would allow a decision to be made about whether to enter students for the AS Mathematics at the end of year 1. To activate the route map open it in Power. Point, click on the Slide Show tab followed by the From Beginning button in the navigation bar. If you want to customise the route map (move topics around/change length of teaching time), please do so before running the slideshow. You can then save your customised version of the route map. Clicking on a topic tile will then give further information about the specification references, specification notes and link to supporting resources. Supporting resources for this teaching route will be available on All About Maths and will be added to the site in time for first teaching. Please note this route map provides a suggested route to teaching the qualification, the topics can be taught in any order over any length of time to suit your own students.

Use of data in statistics The Department for Education (Df. E) have set out the following requirements regarding the use of data in statistics as follows: 9. • • AS and A level mathematics specifications must require students to: become familiar with one or more specific large data set(s) in advance of the final assessment (these data must be real and sufficiently rich to enable the concepts and skills of data presentation and interpretation in the specification to be explored) use technology such as spreadsheets or specialist statistical packages to explore the data set(s) interpret real data presented in summary or graphical form use data to investigate questions arising in real contexts 10. Specifications should require students to explore the data set(s), and associated contexts, during their course of study to enable them to perform tasks that assume familiarity with the contexts, the main features of the data and the ways in which technology can help explore the data. Specifications should also require students to demonstrate the ability to analyse a subset or features of the data using a calculator with standard statistical functions, as detailed in paragraph 8 (please see Df. E content for further information). We encourage the use of statistical data sets and statistical packages throughout the course of study of statistics. In this route map, we have set aside 2 weeks in year 12, weeks 41 and 42, to encourage independent interrogation of data. In week 41, we suggest students study an A-level statistics topic and in week 42, we suggest students complete an activity using statistical packages. Note: It is up teachers to decide which statistics topics to use with statistical data sets and packages. The weeks suggested and the content suggested (N 2 and N 3) are an example.

A-level Mathematics - 2 year Route Map, - AS Maths year 1, A-level Maths year 2 (2017 specification) Algebra & Proof Geometry Calculus Trigonometry Exponentials & Logarithms Sequences & Series Statistics Mechanics Numerical Methods Year 12

A-level Year 1(new spec) – September 2018 (Mon 6&7, Tue 3&4, Wed 1&2) 3 -7 Sept 10 -14 Sept 17 -21 Sept 24 -28 Sept 1 -5 Oct K 1 Statistical Sampling (4) 9. 1 A 1 Proof 1. 1 (4) 29 – 2 Nov 5 – 9 Nov 12 -16 Nov 19 -23 Nov B 5, B 7, B 9 Graphs, Linear & Quadratic Inequalities 1. 7, 2. 4 (12) D 1 Binomial 24 -4 Jan Holiday 7 -11 Jan J 1 -J 4 Vectors 6. 1 - 6. 2 (12) 14 -18 Jan Exam Week 4 -8 Mar 17 -21 June R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) Consolidation 17 -21 Dec G 1 -G 3 Differentiation 4. 1 4. 5 (15) J 1 -J 4 Vectors 6. 1 - 6. 2 (12) 28 -1 Feb 4 -8 Feb 10. 1 – 10. 2 11 -15 Feb P 1 Q 1 – Q 4 Kinematics in one Dimension 7. 1 – 7. 4 (15) 18 -22 Feb Holiday 11 -15 Mar 18 -22 Mar 25 -29 Mar 1 -5 Apr R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) (12) 8 -12 Apr Holiday 15 -19 Apr Holiday 3 -7 June 10 -14 June H 1 -H 3 Integration 4. 6, 4. 7 (12) F 1 – F 3, F 6, F 7 Exponentials & Logarithms 5. 2 – 5. 4 (12) H 1 -H 3 Integration 4. 6, 01 Statistical 4. 7 (12) Hypothesis Testing (9) 11. 1 – 11. 2 10 -14 Dec J 1 -J 4 Vectors 6. 1 - 6. 2 (12) F 1 – F 3, F 6, F 7 Exponentials & Logarithms 5. 2 – 5. 4 P 1 Q 1 – Q 4 Kinematics in one Dimension 7. 1 – 7. 4 22 -26 Apr 3 -7 Dec G 1 -G 3 Differentiation 4. 1 - 4. 5 (15) M 1 N 1 G 1 -G 3 Differentiation 4. 1 4. 5 (15) 26 -30 Nov M 1 N 1 Probability & Statistical Distributions (9) 21 -25 Jan G 1 -G 3 Differentiation 4. 1 4. 5 (15) 25 -1 Mar F 1, F 4, F 5 Logarithms 5. 1 (6) E 1, E 3, E 5, E 7 Trigonometry 3. 1 (9), E 1 Sine ad Cosine rules 3. 2 (3) L 1 -4 Data Presentation & Interpretation (8) 9. 2 -9. 4 22 – 26 Oct Holiday D 1 Binomial Expansions 2. 2 (5) B 6 Polynomials 2. 1, 2. 3 (5) B 1 -B 4 Algebraic Manipulation 1. 2 – 1. 5 (7) 15 -19 Oct 8 -12 Oct B 5, B 7, B 9 Graphs, Linear & Quadratic Inequalities 1. 7, 2. 4 (12) C 1 -C 2 Straight Lines & Circles 1. 6 (8) 29 -3 May 01 Statistical Hypothesis Testing (9) 11. 1 – 11. 2 6 -10 May R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) 13 -17 May 20 -24 May R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) 27 -31 May Holiday 1 -5 July R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) 8 -12 July 15 -19 July Exam Week Consolidation (Y 2 MODULE)J 1, J 5, Q 3 -Q 5 Kinematics in two dimensions Analysis of Data using Statistical N 2 – N 3 Statistical Distributions Packages (18. 1, 18. 3 -18. 4) 24 -28 June R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) 22 -26 July Holiday 29 -2 Aug July Holiday 5 -9 August Holiday

Year 12 (new spec) – September 2017 (Mon 3+4, Tues 6+7, Thurs 1+2) 4 – 8 Sept 11 – 15 Sept 18 – 22 Sept 25 – 29 Sept B 1 -B 4 Algebraic Manipulation 1. 2 – 1. 5 (7) A 1 Proof 1. 1 (4) C 1 -C 2 Straight Lines & Circles 1. 6 (8) 30 – 3 Nov 6 – 10 Nov 13 – 17 Nov 2 – 6 Oct 20 – 24 Nov 27 – 1 Dec E 1, E 3, E 5, E 7 Trigonometry 3. 1 (9), E 1 Sine ad Cosine rules 3. 2 (3) J 1 -J 4 Vectors 6. 1 - 6. 2 (12) B 5, B 7, B 9 Graphs, Linear & Quadratic Inequalities 1. 7, 2. 4 (12) Wed 3 - 5 Jan 8 - 12 Jan Exam Week 26 - 2 Mar 15 – 19 Jan 4 – 8 Dec 5 - 9 Mar F 1 – F 3, F 6, F 7 Exponentials & Logarithms 5. 2 – 5. 4 D 1 Binomial Expansions 2. 2 (5) 23 – 27 Oct Holiday (12) 18 – 19 Dec G 1 -G 3 Differentiation 4. 1 - 4. 5 (15) 22 – 26 Jan K 1 Statistical Sampling (4) 9. 1 12 - 16 Mar 11 – 15 Dec F 1, F 4, F 5 Logarithms 5. 1 (6) 29 - 2 Feb 5 - 9 Feb L 1 -4 Data Presentation & Interpretation (8) 9. 29. 4 19 - 23 Mar 12 – 16 Feb Holiday Consolidation Week G 1 -G 3 Differentiation 4. 1 - 4. 5 (15) 19 - 23 Feb B 6 Polynomials 2. 1, 2. 3 (5) 16 – 20 Oct J 1 -J 4 Vectors 6. 1 - 6. 2 (12) D 1 Binomial Expansions 2. 2 25 - 29 Dec Holiday 9 – 13 Oct 26 - 30 Mar M 1 N 1 Probability & Statistical Distributions (9) 10. 1 – 10. 2 2 – 6 Apr Holiday 9 - 13 Apr Holiday 28 - 1 June Holiday 4 - 8 June P 1 Q 1 – Q 4 Kinematics in one Dimension 7. 1 – 7. 4 (15) H 1 -H 3 Integration 4. 6, 4. 7 (12) Consolidation Starters 16 - 20 Apr M 1 N 1 Probability & Stat Distributi 23 – 27 Apr 30 - 4 May 7 - 11 May 01 Statistical Hypothesis Testing (9) 11. 1 – 11. 2 P 1 Q 1 – Q 4 Kinematics in one Dimension 7. 1 – 7. 4 (15) 14 - 18 May 21 - 25 May N 2 – N 3 Statistical Distributions R 1 – R 4 Forces & Newton’s Laws 8. 1 – 8. 4 (15) Consolidation Starters 11 - 15 June Exam Week 18 - 22 June Analysis of Data using Statistical Packages R 1 – R 4 Forces & Newton’s Laws Consolidation 25 – 29 June AW 2 – 6 July 9 – 13 July 16 – 20 July Analysis of Data using Statistical Packages R 1 – R 4 Forces & Newton’s Laws Consolidation Starters

A-level Mathematics - 2 year Route Map, - AS Maths year 1, A-level Maths year 2 (2017 specification) Year 12 OCTOBER SEPTEMBER Wk 1 Wk 2 Wk 3 Algebraic Manipulation, Quadratic Equations & Simultaneous Equations Wk 4 Straight Lines & Circles Graphs, Linear & Quadratic Inequalities NOVEMBER Wk 11 Integration Wk 5 Wk 6 Binomial Expansi ons Differentiation Wk 12 Wk 13 Trigonometry Wk 22 Wk 23 Exponentials & Logarithms Wk 14 Wk 15 Mock Examinations and Revision Wk 24 Holiday Wk 31 Wk 32 Wk 10 Differentiation Integration Wk 16 Wk 17 Holiday Wk 18 Wk 19 Wk 33 Kinematics in One Dimension Wk 34 Proof MARCH Wk 25 Statistical Sampling Wk 26 Wk 27 Data Presentation & Interpretation Wk 28 Probability & Statistical Distributions Wk 29 Wk 35 Forces & Newton’s Laws Wk 43 Wk 44 Wk 30 Statistical Hypothesis Testing Holiday JUNE Wk 36 Wk 37 Summer Examinations and Revision Wk 38 Holiday Wk 39 Wk 40 Summer Examinations and Revision JULY Wk 42 Wk 20 Vectors MAY JUNE Statistical Distributions Wk 9 JANUARY APRIL Wk 41 Holiday FEBRUARY Wk 21 Wk 8 DECEMBER JANUARY Holiday Wk 7 NOVEMBER Wk 45 Analysis of Data using Statistical Packages Year 13

A-level Mathematics - 2 year Route Map, - AS Maths year 1, A-level Maths year 2 (2017 specification) Year 13 OCTOBER SEPTEMBER Wk 1 Wk 2 Wk 3 Wk 4 Trigonometry & Circular Measure Binomial Theorem, Sequences & Series Wk 5 Wk 7 Further Differentiation Functions & Transformations NOVEMBER Wk 11 Wk 6 Numerical Methods Wk 13 Parametric Equations JANUARY Wk 22 Wk 23 Holiday Differential Equations Wk 14 Wk 15 Wk 16 Mock Examinations and Revision Wk 17 Holiday Wk 32 Further Integration Wk 18 Wk 19 Trigonometry Wk 24 Wk 25 Kinematics in Two Dimensions Statistical Distributions Wk 34 Statistical Hypothesis Testing JUNE Wk 26 Equilibrium & Resolving Wk 27 Statics & Dynamics Wk 28 Moments Wk 29 Wk 35 Revision Wk 42 Summer Examinations and Revision Wk 43 Wk 44 Wk 30 Holiday JUNE Wk 36 Wk 37 Summer Examinations and Revision Wk 38 Holiday Wk 39 Wk 40 Summer Examinations and Revision JULY Wk 41 Wk 20 Partial Fractions & Integration MAY Wk 33 Wk 10 MARCH APRIL Further Probability Holiday Wk 9 JANUARY FEBRUARY Wk 31 Wk 8 DECEMBER Wk 12 Wk 21 NOVEMBER Wk 45 Year 12

Year 12 Return to Routemap

Algebraic Manipulation, Quadratic Equations and Simultaneous Equations (slide 1 of 2) Continued on next page B 1 Specification content: Specification notes: Ø [Understand use the laws of indices for all rational Chapter 1. 2 exponents] Ø [Use and manipulate surds, including rationalising the B 2 Chapter 1. 3 denominator] Ø [Work with quadratic functions and their graphs; the discriminant of a quadratic function, including the B 3 conditions for real and repeated roots; completing the square; solution of quadratic equations including solving quadratic equations in a function of the unknown] Return to Routemap Chapter 1. 4

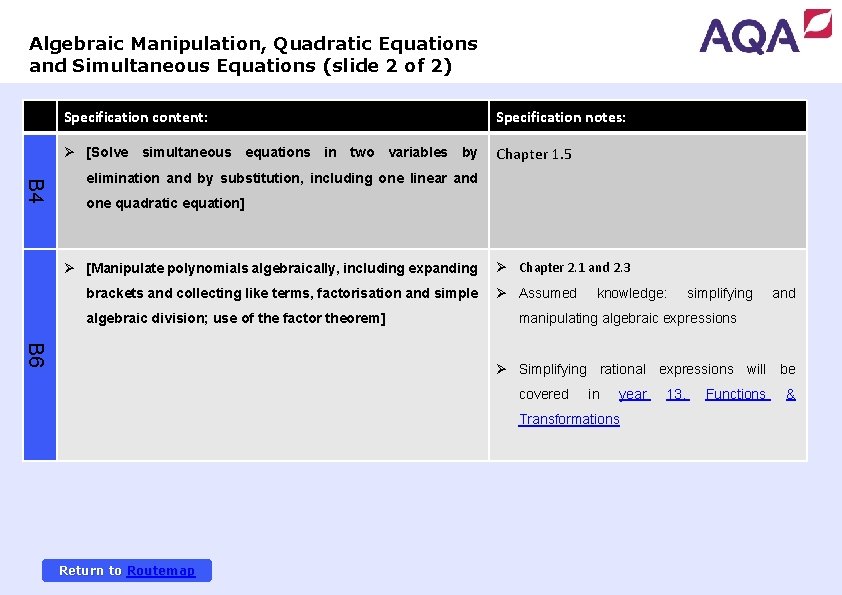
Algebraic Manipulation, Quadratic Equations and Simultaneous Equations (slide 2 of 2) Specification content: Specification notes: Ø [Solve simultaneous equations in two variables by Chapter 1. 5 B 4 elimination and by substitution, including one linear and one quadratic equation] Ø [Manipulate polynomials algebraically, including expanding brackets and collecting like terms, factorisation and simple algebraic division; use of the factor theorem] Ø Chapter 2. 1 and 2. 3 Ø Assumed knowledge: simplifying and manipulating algebraic expressions B 6 Ø Simplifying rational expressions will be covered in year Transformations Return to Routemap 13, Functions &

Graphs, Linear & Quadratic Inequalities (slide 1 of 3) Specification content: Continued on next page Specification notes: Chapter 1. 7 B 5 Return to Routemap

Graphs, Linear & Quadratic Inequalities (slide 2 of 3) Specification content: Continued on next page Specification notes: Ø Chapter 2. 4 (also B 9) Ø Assumed knowledge: linear graphs, quadratic graphs, simple cubic graphs and reciprocal graphs B 7 Ø The modulus function will be covered in year 13, Functions & Transformations Return to Routemap

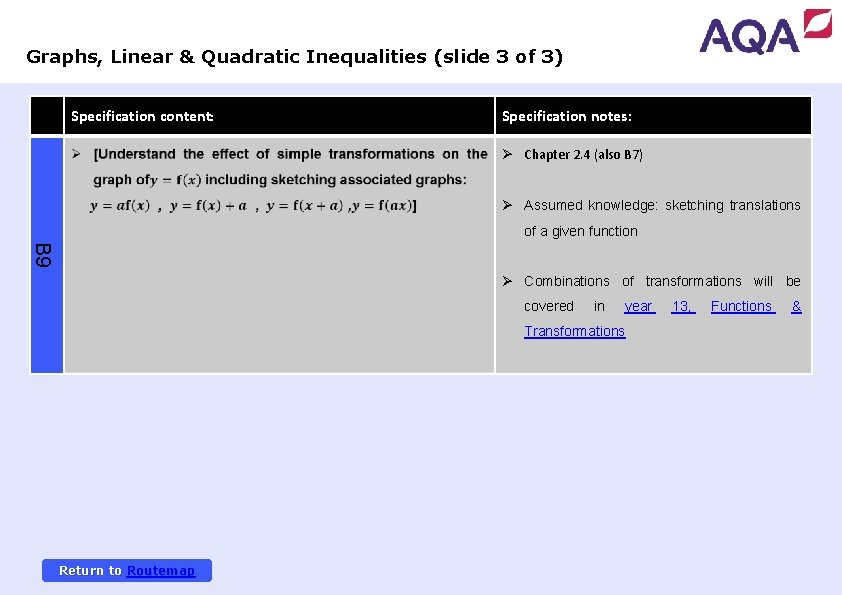
Graphs, Linear & Quadratic Inequalities (slide 3 of 3) Specification content: Specification notes: Ø Chapter 2. 4 (also B 7) Ø Assumed knowledge: sketching translations of a given function B 9 Ø Combinations of transformations will be covered in year Transformations Return to Routemap 13, Functions &

Straight Lines & Circles (slides 1 of 2) Specification content: Continued on next page Specification notes: Chapter 1. 6 (also C 2) C 1 Return to Routemap

Straight Lines & Circles (slide 2 of 2) Specification content: Specification notes: Chapter 1. 6 (also C 1) C 2 Return to Routemap

Binomial Expansions Specification content: D 1 Return to Routemap Specification notes:

Differentiation (slide 1 of 2) Specification content: Continued on next page Specification notes: G 1 Chapter 4. 1 Return to Routemap

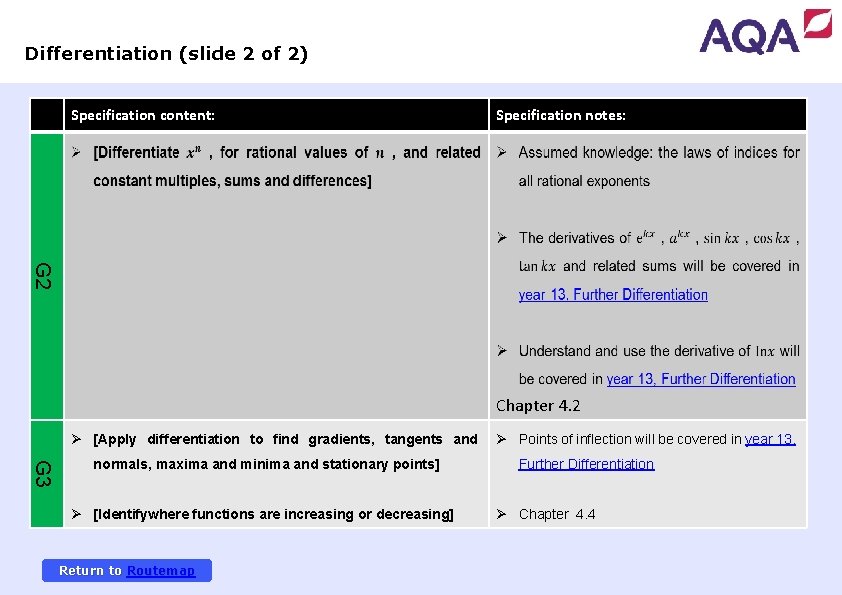
Differentiation (slide 2 of 2) Specification content: Specification notes: G 2 Chapter 4. 2 Ø [Apply differentiation to find gradients, tangents and G 3 normals, maxima and minima and stationary points] Ø [Identifywhere functions are increasing or decreasing] Return to Routemap Ø Points of inflection will be covered in year 13, Further Differentiation Ø Chapter 4. 4

Integration Specification notes: Ø [Know and use the Fundamental Theorem of Calculus] Chapter 4. 6 (and H 2) Ø [Evaluate definite integrals; use a definite integral to find Ø The area bounded by two curves will be H 1 Specification content: H 2 H 3 the area under a curve] covered in year 13, Further Integration Ø Chapter 4. 7 Return to Routemap

Trigonometry (slide 1 of 2) Specification content: Continued on next page Specification notes: Ø Chapter 3. 1 (also E 5, E 7) Ø Assumed knowledge: sine, cosine and tangent as the ratios of sides of a right-angled E 1 triangle Ø The use of radians will be covered in year 13, Trigonometry & Circular Measure Ø [Understand use the sine, cosine and tangent E 3 functions; their graphs, symmetries and periodicity] Ø Chapter 3. 2 Ø The exact values of sine, cosine and tangent for common values will be covered in year 13, Trigonometry & Circular Measure Ø Chapter 3. 1 (also E 1, E 7) E 5 Ø The identities involving secant, cosecant and cotangent will be covered in year 13, Trigonometry & Circular Measure Return to Routemap

Trigonometry (slide 2 of 2) Continued on next page Specification content: Specification notes: Ø [Solve simple trigonometric equations in a given interval, Ø Chapter 3. 1 (also E 1, E 5) E 7 including quadratic equations in sin, cos and tan and equations involving multiples of the unknown angle] Return to Routemap

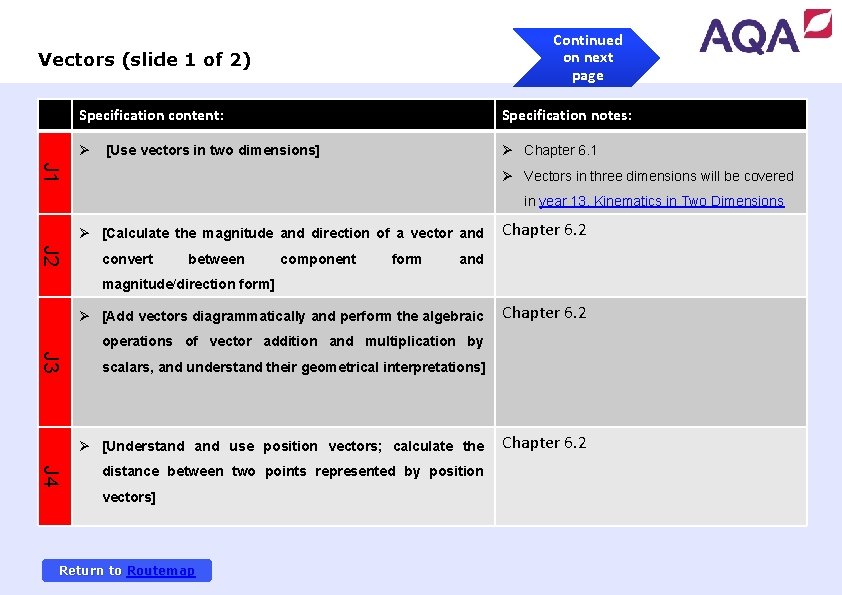
Continued on next page Vectors (slide 1 of 2) Specification content: Specification notes: Ø Ø Chapter 6. 1 [Use vectors in two dimensions] J 1 Ø Vectors in three dimensions will be covered in year 13, Kinematics in Two Dimensions Ø [Calculate the magnitude and direction of a vector and J 2 convert between component form Chapter 6. 2 and magnitude/direction form] Ø [Add vectors diagrammatically and perform the algebraic Chapter 6. 2 operations of vector addition and multiplication by J 3 scalars, and understand their geometrical interpretations] Ø [Understand use position vectors; calculate the J 4 distance between two points represented by position vectors] Return to Routemap Chapter 6. 2

Vectors (slides 2 of 2) Specification content: Specification notes: Ø [Use vectors to solve problems in pure mathematics and Ø Chapter 8. 1 J 5 in context, including forces] Ø The use of vectors in kinematics problems will be covered in year 13, Kinematics in Two Dimensions Return to Routemap

Proof Specification content: Specification notes: Chapter 1. 1 A 1 Return to Routemap

Exponentials & Logarithms (slides 1 of 3) Specification content: F 1 F 2 Return to Routemap Continued on next page Specification notes:

Exponentials & Logarithms (slides 2 of 3) Specification content: Continued on next page Specification notes: F 3 Ø Assumed knowledge: the laws of indices for all rational exponents F 4 Return to Routemap

Exponentials & Logarithms (slides 3 of 3) Specification content: F 5 F 6 Ø [Understand use exponential growth and decay; use in modelling (examples may include the use of ein F 7 continuous compound interest, radioactive decay, drug concentration decay, exponential growth as a model for population growth); consideration of limitations and refinements of exponential models] Return to Routemap Specification notes:

Continued on next page Statistical Sampling Specification content: Specification notes: Ø [Understand use the terms ‘population’ and Ø See slide 2 ‘sample’] Ø Assumed knowledge: application of basic Ø [Use samples to make informal inferences about the population] K 1 Ø [Understand use sampling techniques, including simple random sampling and opportunity sampling] Ø [Select or critique sampling techniques in the context of solving a statistical problem, including understanding that different samples can lead to different conclusions about the population] Return to Routemap statistics to describe a population

Data Presentation and Interpretation (slide 1 of 3) Continued on next page Specification content: Specification notes: Ø [Interpret diagrams for single-variable data, including Ø See slide 2 L 1 understanding that area in a histogram represents frequency] Ø [Connect to probability distributions] Return to Routemap

Data Presentation and Interpretation (slide 2 of 3) Continued on next page Specification content: Specification notes: Ø [Interpret scatter diagrams and regression lines for Ø See slide 2 bivariate data, including recognition of scatter diagrams which include distinct sections of the population (calculations involving regression lines are excluded)] L 2 Ø [Understand informal interpretation of correlation] Ø [Understand that correlation does not imply causation] Return to Routemap Ø Assumed knowledge: recognise correlation and know that it does not indicate causation

Data Presentation and Interpretation (slide 3 of 3) Continued on next page Specification content: Specification notes: Ø [Interpret measures of central tendency and variation, Ø See slide 2 extending to standard deviation] L 3 Ø Assumed knowledge: quartiles and interØ [Be able to calculate standard deviation, including from quartile range summary statistics] Ø [Recognise and interpret possible outliers in data sets and statistical diagrams] L 4 Ø [Select or critique data presentation techniques in the context of a statistical problem] Ø [Be able to clean data, including dealing with missing data, errors and outliers] Return to Routemap Ø See slide 2

Continued on next page Probability and Statistical Distributions Specification content: Ø [Understand Specification notes: use mutually exclusive and Ø See slide 2 independent events when calculating probabilities] M 1 Ø Assumed knowledge: the 0 to 1 probability Ø [Link to discrete and continuous distributions] Ø [Understand use simple, discrete probability distributions (calculation of mean and variance of N 1 discrete random variables is excluded), including the binomial distribution, as a model; calculate probabilities using the binomial distribution] Return to Routemap scale Ø See slide 2

Continued on next page Statistical Hypothesis Testing Specification content: Specification notes: Ø [Understand apply the language of statistical Ø See slide 2 hypothesis testing, developed through a binomial model: O 1 null hypothesis, alternative hypothesis, significance Ø The use of correlation coefficients in level, test statistic, 1 -tail test, 2 -tail test, critical value, hypothesis testing will be covered in year 13, critical region, acceptance region, p-value] Statistical Hypothesis Testing Ø [Conduct a statistical hypothesis test for the proportion in the binomial distribution and interpret the results in context] O 2 Ø [Understand that a sample is being used to make an inference about the population and appreciate that the significance level is the probability of incorrectly rejecting the null hypothesis] Return to Routemap Ø See slide 2

Kinematics in One Dimension (slide 1 of 2) Continued on next page Specification content: Specification notes: Ø [Understand use fundamental quantities and units in Ø Chapter 7. 1 the S. I. system: length, time, mass] Ø Moments be covered in year 13, Moments P 1 Ø [Understand use derived quantities and units: velocity, acceleration, force, weight] Ø [Understand use the language of kinematics: Q 1 position; displacement; distance travelled; velocity; speed; acceleration] Return to Routemap Ø Chapter 7. 2

Kinematics in One Dimension (slide 2 of 2) Specification content: Specification notes: Ø [Understand, use and interpret graphs in kinematics for Ø Chapter 7. 2 motion in a straight line: displacement against time and Q 2 interpretation of gradient; velocity against time and interpretation of gradient and area under the graph] Ø [Understand, use and derive the formulae for constant Q 3 acceleration for motion in a straight line] Ø Chapter 7. 3 Ø The extension to two dimensions will be covered in year 13, Kinematics in Two Dimensions Ø Chapter 7. 4 Ø The extension to use calculus techniques for Q 4 motion in two dimensions using vectors will be covered in year 13, Kinematics in Two Dimensions Return to Routemap

Forces and Newton’s Laws (slide 1 of 3) Continued on next page R 1 Specification content: Specification notes: Ø [Understand the concept of a force; understand use Ø Chapter 8. 1 Newton’s first law] Ø [Understand use Newton’s second law for motion in a Ø Chapter 8. 2 R 2 straight line (restricted to forces in two perpendicular Ø The extension to situations where forces directions or simple cases of forces given as 2 -D vectors)] need to be resolved in two dimensions will be covered in year 13, Equilibrium & Resolving Return to Routemap

Forces and Newton’s Laws (slide 2 of 3) Continued on next page Specification content: Specification notes: Ø [Understand use weight and motion in a straight line Ø Chapter 8. 3 under gravity; gravitational acceleration, g , and its value in S. I. units to varying degrees of accuracy] R 3 [(the inverse square law for gravitation is not required and g may be assumed to be constant, but students should be aware that g is not a universal constant but depends on location)] Return to Routemap

Forces and Newton’s Laws (slide 3 of 3) Specification content: Specification notes: Ø [Understand use Newton’s third law; equilibrium of Ø Chapter 8. 4 R 4 forces on a particle and motion in a straight line (restricted Ø Resolving forces in two dimensions and the to forces in two perpendicular directions or simple cases equilibrium of a particle under coplanar of forces given as 2 -D vectors); application to problems forces involving smooth pulleys and connected particles] Equilibrium & Resolving Return to Routemap will be covered in year 13,

Continued on next page Statistical Distributions Specification content: Specification notes Ø Understand use the Normal distribution as a model; find Ø See slide 2 probabilities using the Normal distribution N 2 Ø Note that N 2 and N 3 will be covered again in Ø Link to histograms, mean, standard deviation, points of year 13, Statistical Distributions inflection and the binomial distribution Ø Select an appropriate probability distribution for a context, N 3 with appropriate reasoning, including recognising when the binomial or Normal model may not be appropriate Return to Routemap Ø See slide 2

Analysis of Data using Statistical Packages Specification content: Ø See slide 2 Return to Routemap Continued on next page Specification notes

Year 13 Return to Routemap

Binomial Theorem, Sequences & Series (slide 1 of 2) Specification content: Continued on next page Specification notes: Ø Assumed knowledge: covered in year 12, D 1 Binomial Expansions D 2 D 3 Ø Understand use sigma notation for sums of series Return to Routemap

Binomial Theorem, Sequences & Series (slide 2 of 2) Specification content: D 4 D 5 D 6 Ø Use sequences and series in modelling Return to Routemap Specification notes:

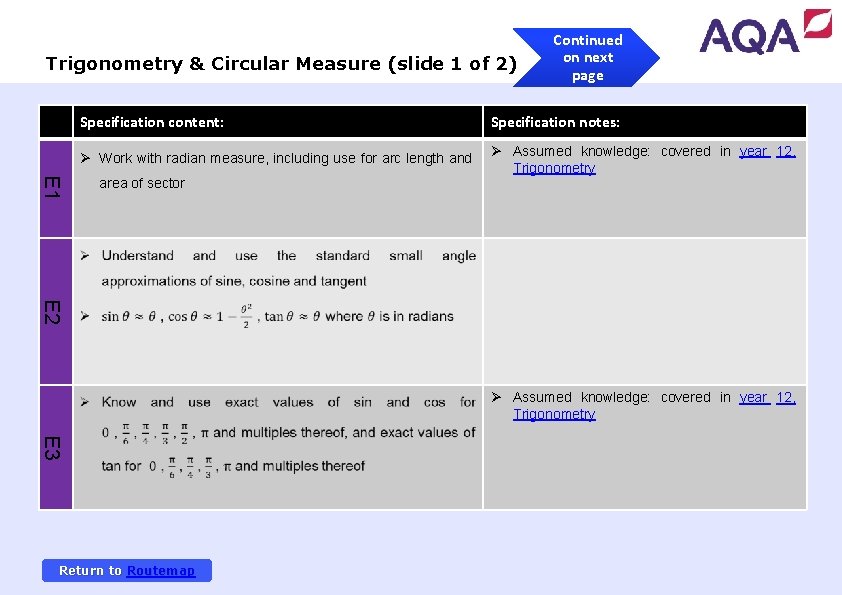
Trigonometry & Circular Measure (slide 1 of 2) Continued on next page E 1 Specification content: Specification notes: Ø Work with radian measure, including use for arc length and Ø Assumed knowledge: covered in year 12, Trigonometry area of sector E 2 Ø Assumed knowledge: covered in year 12, Trigonometry E 3 Return to Routemap

Trigonometry & Circular Measure (slide 2 of 2) Specification content: Specification notes: Ø Understand use the definitions of secant, cosecant and cotangent and of arcsin, arccos and arctan; their relationships to sine, cosine and tangent; understanding of E 4 their graphs; their ranges and domains Ø Assumed knowledge: covered in year 12, Trigonometry E 5 Return to Routemap

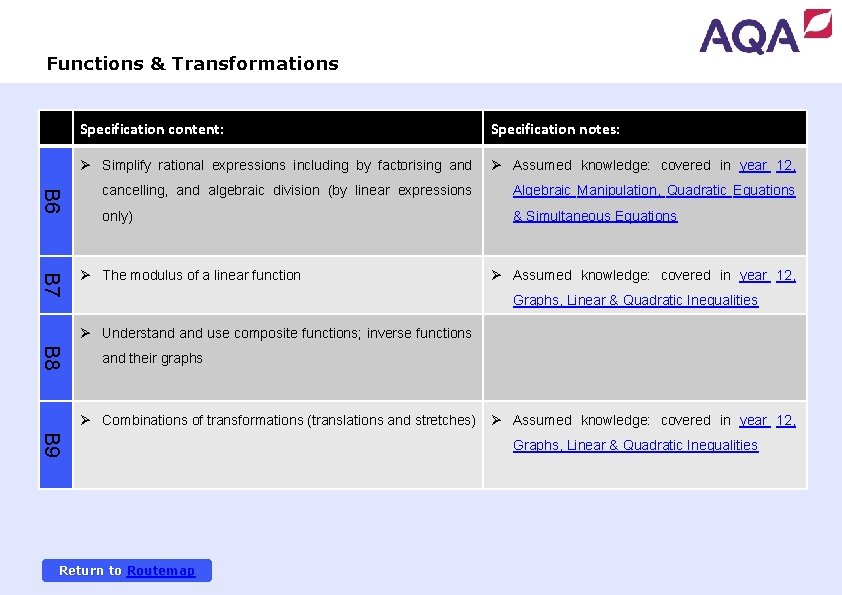
Functions & Transformations B 6 Specification content: Specification notes: Ø Simplify rational expressions including by factorising and Ø Assumed knowledge: covered in year 12, cancelling, and algebraic division (by linear expressions Algebraic Manipulation, Quadratic Equations only) & Simultaneous Equations B 7 Ø The modulus of a linear function Ø Assumed knowledge: covered in year 12, Graphs, Linear & Quadratic Inequalities Ø Understand use composite functions; inverse functions B 8 and their graphs Ø Combinations of transformations (translations and stretches) Ø Assumed knowledge: covered in year 12, B 9 Return to Routemap Graphs, Linear & Quadratic Inequalities

Further Differentiation (slide 1 of 2) Specification content: Continued on next page Specification notes: Ø Assumed knowledge: covered in year 12, Differentiation G 1 Ø Assumed knowledge: covered in year 12, G 2 Differentiation G 3 Ø Apply differentiation to find points of inflection Return to Routemap Ø Assumed knowledge: covered in year 12, Differentiation

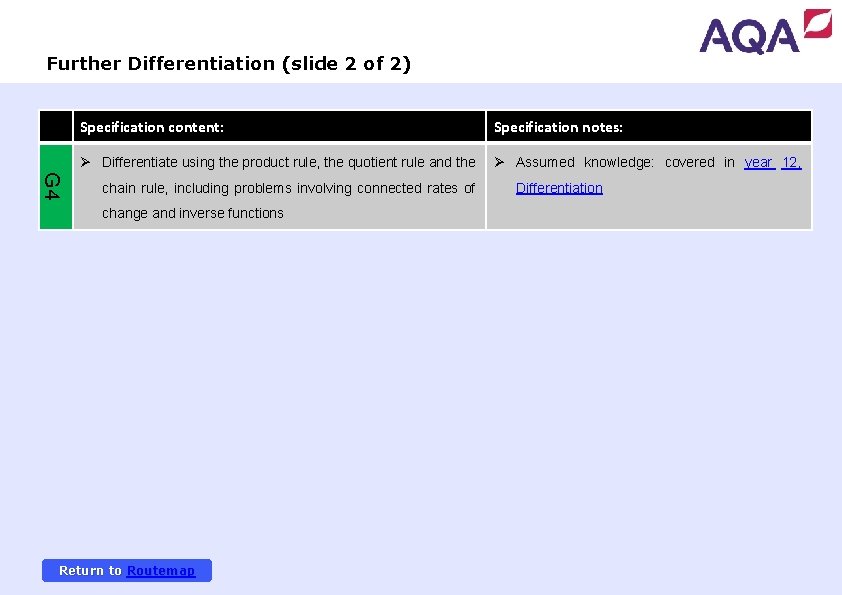
Further Differentiation (slide 2 of 2) Specification content: Specification notes: Ø Differentiate using the product rule, the quotient rule and the Ø Assumed knowledge: covered in year 12, G 4 chain rule, including problems involving connected rates of change and inverse functions Return to Routemap Differentiation

Further Integration (slide 1 of 2) Specification content: Continued on next page Specification notes: Ø Assumed knowledge: covered in year 12, H 2 Integration Ø Use a definite integral to find the area between two curves H 3 Ø Understand use integration as the limit of a sum H 4 Return to Routemap Ø Assumed knowledge: covered in year 12, Integration

Further Integration (slide 2 of 2) Specification content: Specification notes: Ø Carry out simple cases of integration by substitution and integration by parts; understand these methods as the inverse processes of the chain and product rules respectively H 5 (Integration by substitution includes finding a suitable substitution and is limited to cases where one substitution will lead to a function which can be integrated; integration by parts includes more than one application of the method but excludes reduction formulae) Return to Routemap

Numerical Methods (slide 1 of 2) Specification content: I 1 I 2 Return to Routemap Continued on next page Specification notes:

Numerical Methods (slide 2 of 2) Specification content: Ø Understand use numerical integration of functions, including the use of the trapezium rule and estimating the I 3 approximate area under a curve and limits that it must lie between Ø Use numerical methods to solve problems in context I 4 Return to Routemap Specification notes:

Parametric Equations Specification content: Ø Understand use the parametric equations of curves and C 3 conversion between Cartesian and parametric forms Ø Use parametric equations in modelling in a variety of C 4 contexts Ø Differentiate simple functions and relations defined implicitly G 5 or parametrically, for first derivative only Return to Routemap Specification notes:

Trigonometry Specification content: E 6 E 8 Ø Construct proofs involving trigonometric functions and identities Return to Routemap Specification notes:

Partial Fractions & Integration Specification content: Ø Decompose rational Specification notes: functions into partial fractions (denominators not more complicated than squared linear B 10 terms and with no more than 3 terms, numerators constant or linear) Ø Integrate using partial fractions that are linear in the H 6 denominator Return to Routemap

Differential Equations (slide 1 of 2) Specification content: B 11 Ø Use of functions in modelling, including consideration of limitations and refinements of the models Ø Differentiate simple functions and relations defined implicitly, G 5 for first derivative only Ø Construct simple differential equations in pure mathematics G 6 and in context, (contexts may include kinematics, population growth and modelling the relationship between price and demand) Return to Routemap Continued on next page Specification notes:

Differential Equations (slide 2 of 2) Specification content: Ø Evaluate the analytical solution of simple first order differential equations with separable variables, including H 7 finding particular solutions (Separation of variables may require factorisation involving a common factor) Ø Interpret the solution of a differential equation in the context H 8 of solving a problem, including identifying limitations of the solution; includes links to kinematics Return to Routemap Specification notes:

Kinematics in Two Dimensions (slide 1 of 2) Continued on next page J 1 Specification content: Specification notes: Ø Use vectors in three dimensions Ø Assumed knowledge: covered in year 12, Vectors J 5 Ø Use vectors to solve problems in kinematics Ø Assumed knowledge: covered in year 12, Vectors Ø Use trigonometric functions to solve problems in context, E 9 including problems involving vectors, kinematics and forces Ø Understand, use and derive the formulae for constant Q 3 acceleration for motion in 2 dimensions using vectors Return to Routemap Ø Assumed knowledge: covered in year 12, Kinematics in One Dimension

Kinematics in Two Dimensions (slide 2 of 2) Specification content: Specification notes: Ø Use calculus in kinematics for motion in 2 dimensions using Ø Assumed knowledge: covered in year 12, Q 4 vectors Ø Model motion under gravity in a vertical plane using vectors; Q 5 projectiles Return to Routemap Kinematics in One Dimension

Equilibrium and Resolving Specification content: Specification notes: Ø Understand use Newton’s second law for motion in Ø Assumed knowledge: covered in year 12, R 2 situations where forces need to be resolved (restricted to 2 Forces & Newton’s Laws dimensions) Ø Resolving forces in 2 dimensions; equilibrium of a particle R 4 under coplanar forces Return to Routemap Ø Assumed knowledge: covered in year 12, Forces & Newton’s Laws

Statics and Dynamics Specification content: Ø Understand use addition of forces; resultant forces; R 5 dynamics for motion in a plane R 6 Return to Routemap Specification notes:

Moments Specification content: Specification notes: Ø Understand use derived quantities and units: moment Ø Assumed knowledge: covered in year 12, P 1 Kinematics in One Dimension Ø Understand use moments in simple static contexts S 1 Return to Routemap

Continued on next page Further Probability Specification content: Specification notes: Ø See slide 2 M 3 Ø Modelling with probability, including critiquing assumptions made and the likely effect of more realistic assumptions Return to Routemap Ø See slide 2

Continued on next page Statistical Distributions Specification content: Specification notes Ø Understand use the Normal distribution as a model; find Ø See slide 2 probabilities using the Normal distribution N 2 Ø Link to histograms, mean, standard deviation, points of inflection and the binomial distribution Ø Select an appropriate probability distribution for a context, N 3 with appropriate reasoning, including recognising when the binomial or Normal model may not be appropriate Return to Routemap

Continued on next page Statistical Hypothesis Testing Specification content: Specification notes Ø Understand apply correlation coefficients as measures of Ø See slide 2 how close data points lie to a straight line and be able to interpret a given correlation coefficient using a given p-value O 1 or critical value (calculation of correlation coefficients is Ø Assumed knowledge: covered in year 12, Statistical Hypothesis Testing excluded) Ø Conduct a statistical hypothesis test for the mean of a Normal distribution with known, given or assumed variance and O 3 interpret the results in context Return to Routemap Ø See slide 2