AKM 205 AKIKANLAR MEKAN BOYUT ANALZ Yrd Do

AKM 205 AKIŞKANLAR MEKANİĞİ “BOYUT ANALİZİ” Yrd. Doç. Dr. Onur Tunçer İstanbul Teknik Üniversitesi

Outline A. B. C. D. E. F. G. What’s the secret of being a Scientist or an Engineer? What are Units and Dimensions anyway? What is Dimensional Analysis and why should I care? Why aren’t there any mice in the Polar Regions? Why was Gulliver driven out of Lillipute? What if Pythagorus had known Dimensional Analysis? But what do I really need to know about Dimensional Analysis so that I can pass the test? H. Can I get into trouble with Dimensional Analysis? The ballad of G. I. Taylor. I. But can it be used in the Lab ?

How to be a Scientist or Engineer The steps in understanding and/or control any physical phenomena is to 1. Identify the relevant physical variables. 2. Relate these variables using the known physical laws. 3. Solve the resulting equations. Secret #1: Usually not all of these are possible. Sometimes none are.

ALL IS NOT LOST BECAUSE OF Secret #2: Dimensional Analysis Rationale • Physical laws must be independent of arbitrarily chosen units of measure. Nature does not care if we measure lengths in centimeters or inches or light-years or … • Check your units! All natural/physical relations must be dimensionally correct.

Dimensional Analysis refers to the physical nature of the quantity and the type of unit (Dimension) used to specify it. • Distance has dimension L. • Area has dimension L 2. • Volume has dimension L 3. • Time has dimension T. • Speed has dimension L/T

Why are there no small animals in the polar regions? • Heat Loss Surface Area (L 2) • Mass Volume (L 3) • Heat Loss/Mass Area/Volume = L 2 / L 3 = L-1

Heat Loss/Mass Area/Volume = L 2/ L 3 = L-1 Mouse (L = 5 cm) 1/L = 1/(0. 05 m) = 20 m-1 20 : 0. 5 or Polar Bear (L = 2 m) 1/L = 1/(2 m) = 0. 5 m-1 40 : 1

Gulliver’s Travels: Dimensional Analysis • Gulliver was 12 x the Lilliputians • How much should they feed him? 12 x their food ration? • A persons food needs are related to their mass (volume) – This depends on the cube of the linear dimension.

Let LG and VG denote Gulliver’s linear and volume dimensions. Let LL and VL denote the Lilliputian’s linear and volume dimensions. Gulliver is 12 x taller than the Lilliputians, LG =12 LL Now VG (LG)3 and VL (LL)3, so VG / VL = (LG)3 / (LL)3 = (12 LL)3 / (LL)3 = 123 = 1728 Gulliver needs to be fed 1728 times the amount of food each day as the Lilliputians. This problem has direct relevance to drug dosages in humans

Dimensions of Some Common Physical Quantities [x], Length – L [m], Mass – M [t], Time – T [v], Velocity – LT-1 [a], Acceleration – LT-2 [F], Force – MLT-2 [r], Mass Density – ML-3 [P], Pressure – ML-1 T-2 [E], Energy – ML 2 T-2 [I], Electric Current – QT-1 [q], Electric Change – Q [E], Electric Field - MLQT-2 All are powers of the fundamental dimensions: [Any Physical Quantity] = Ma. Lb. Tc. Qd

Dimensional Analysis Theorems • Dimensional Homogeneity Theorem: Any physical quantity is dimensionally a power law monomial - [Any Physical Quantity] = Ma. Lb. Tc. Qd • Buckingham Pi Theorem: If a system has k physical quantities of relevance that depend on r independent dimensions, then there a total of k-r independent dimensionless products p 1, p 2, …, pk-r. The behavior of the system is describable by a dimensionless equation F(p 1, p 2, …, pk-r)=0

Exponent Method 1. 2. 3. 4. 5. 6. 7. 8. List all k variables involved in the problem Express each variables in terms of [M] [L] [T ] dimensions (r) Determine the required number of dimensionless parameters (k – r) Select a number of repeating variables = r (All dimensions must be included in this set and each repeating variable must be independent of the others. ) Form a dimensionless parameter p by multiplying one of the non-repeating variables by the product of the repeating variables, each raised to an unknown exponent. Solved for the unknown exponents. Repeat this process for each non-repeating variable Express result as a relationship among the dimensionless parameters – F(p 1, p 2, p 3, …) = 0.

G. I. Taylor’s 1947 Analysis Published U. S. Atomic Bomb was 18 kiloton device

Nuclear Explosion Shock Wave The propagation of a nuclear explosion shock wave depends on: E, r, r, and t. n=4 No. of variables r=3 No. of dimensions n – r = 1 No. of dimensionless parameters E r r t ML 2 T-2 ML-3 L T Select “repeating” variables: E, t, and r Combine these with the rest of the variables: r

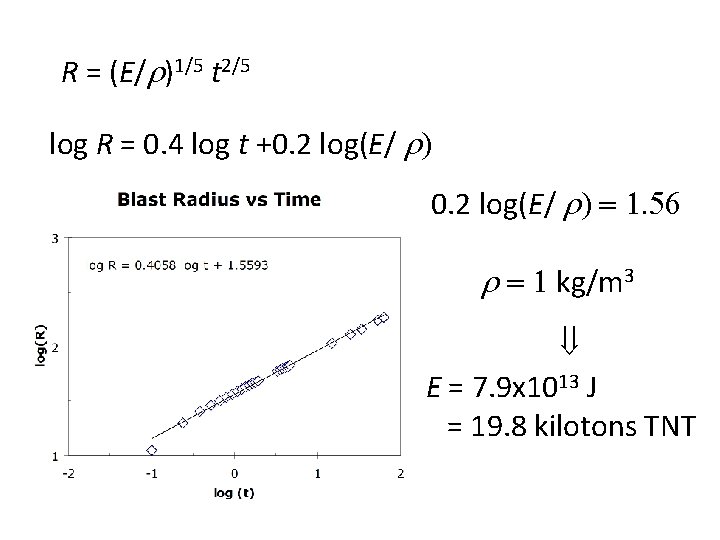
R = (E/r)1/5 t 2/5 log R = 0. 4 log t +0. 2 log(E/ r) = 1. 56 r = 1 kg/m 3 E = 7. 9 x 1013 J = 19. 8 kilotons TNT

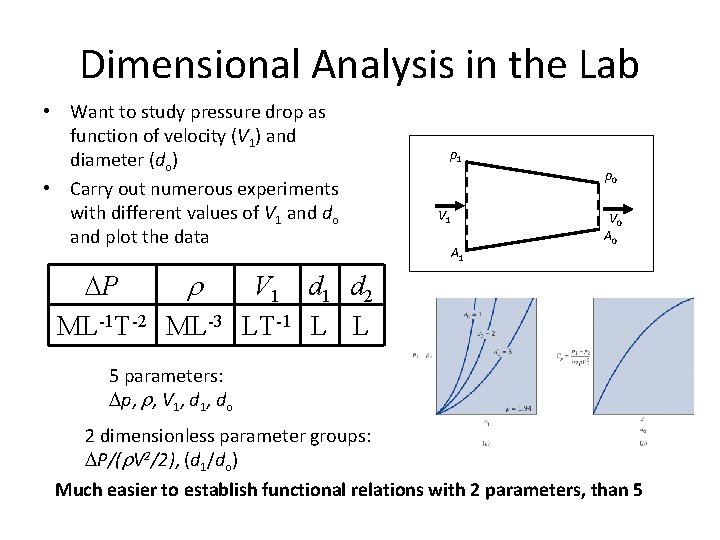
Dimensional Analysis in the Lab • Want to study pressure drop as function of velocity (V 1) and diameter (do) • Carry out numerous experiments with different values of V 1 and do and plot the data p 1 p 0 V 1 A 1 V 0 A 0 DP V 1 d 2 r ML-1 T-2 ML-3 LT-1 L L 5 parameters: Dp, r, V 1, do 2 dimensionless parameter groups: DP/(r. V 2/2), (d 1/do) Much easier to establish functional relations with 2 parameters, than 5

Flow Similarity and Model Testing • Geometrical similarity: similar geometry. • Kinematic similarity: flow pattern around the model should be similar to. . . • Dynamical similarity: forces acting on the model should be similar to the real object to be analyzed. Flight test of a F-18 model in NASA 11 ft transonic (Mach. 4 -1. 5) wind tunnel NASA NFAC Wind Tunnel

Nature of Dimensional Analysis Example: Drag on a Sphere ü Drag depends on FOUR parameters: sphere size (D); speed (V); fluid density (r); fluid viscosity (m) ü Difficult to know how to set up experiments to determine dependencies ü Difficult to know how to present results (four graphs? )

Nature of Dimensional Analysis Example: Drag on a Sphere ü Only one dependent and one independent variable ü Easy to set up experiments to determine dependency ü Easy to present results (one graph)

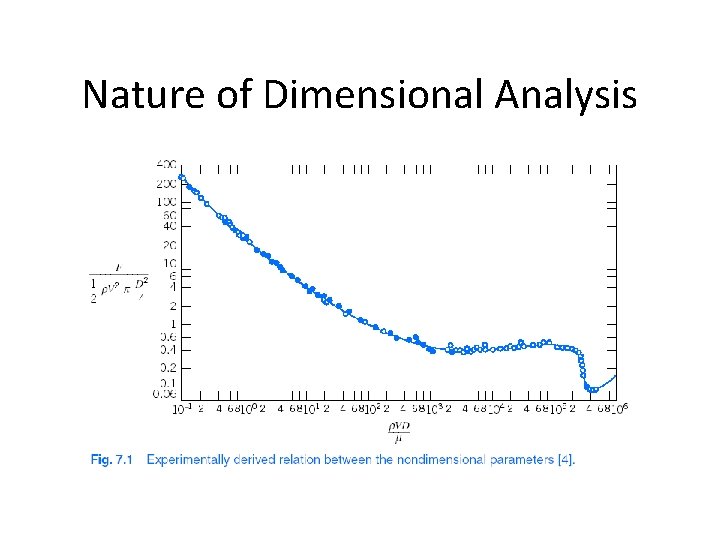
Nature of Dimensional Analysis

Buckingham Pi Theorem • Step 1: List all the dimensional parameters involved Let n be the number of parameters Example: For drag on a sphere, F, V, D, r, m, and n = 5

Buckingham Pi Theorem • Step 2 Select a set of fundamental (primary) dimensions For example MLt, or FLt Example: For drag on a sphere choose MLt

Buckingham Pi Theorem • Step 3 List the dimensions of all parameters in terms of primary dimensions Let r be the number of primary dimensions Example: For drag on a sphere r = 3

Buckingham Pi Theorem • Step 4 Select a set of r dimensional parameters that includes all the primary dimensions Example: For drag on a sphere (m = r = 3) select r, V, D

Buckingham Pi Theorem • Step 5 Set up dimensional equations, combining the parameters selected in Step 4 with each of the other parameters in turn, to form dimensionless groups There will be n – m equations Example: For drag on a sphere

Buckingham Pi Theorem • Step 5 (Continued) Example: For drag on a sphere

Buckingham Pi Theorem • Step 6 Check to see that each group obtained is dimensionless Example: For drag on a sphere

Significant Dimensionless Groups in Fluid Mechanics • Reynolds Number ü Mach Number

Significant Dimensionless Groups in Fluid Mechanics • Froude Number ü Weber Number

Significant Dimensionless Groups in Fluid Mechanics • Euler Number ü Cavitation Number

Flow Similarity and Model Studies • Geometric Similarity – Model and prototype have same shape – Linear dimensions on model and prototype correspond within constant scale factor • Kinematic Similarity – Velocities at corresponding points on model and prototype differ only by a constant scale factor • Dynamic Similarity – Forces on model and prototype differ only by a constant scale factor

Flow Similarity and Model Studies • Example: Drag on a Sphere

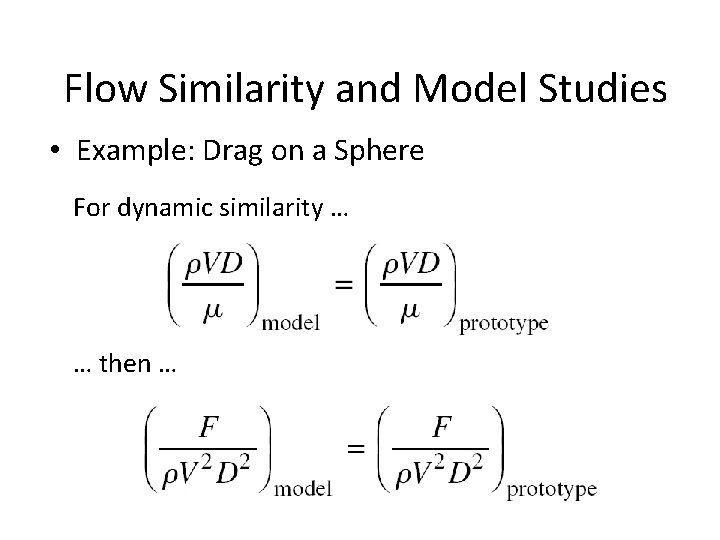
Flow Similarity and Model Studies • Example: Drag on a Sphere For dynamic similarity … … then …

Flow Similarity and Model Studies • Incomplete Similarity Sometimes (e. g. , in aerodynamics) complete similarity cannot be obtained, but phenomena may still be successfully modelled

Flow Similarity and Model Studies • Scaling with Multiple Dependent Parameters Example: Centrifugal Pump Head Pump Power

Flow Similarity and Model Studies • Scaling with Multiple Dependent Parameters Example: Centrifugal Pump Head Coefficient Power Coefficient

Flow Similarity and Model Studies • Scaling with Multiple Dependent Parameters Example: Centrifugal Pump (Negligible Viscous Effects) If … … then …

Flow Similarity and Model Studies • Scaling with Multiple Dependent Parameters Example: Centrifugal Pump Specific Speed

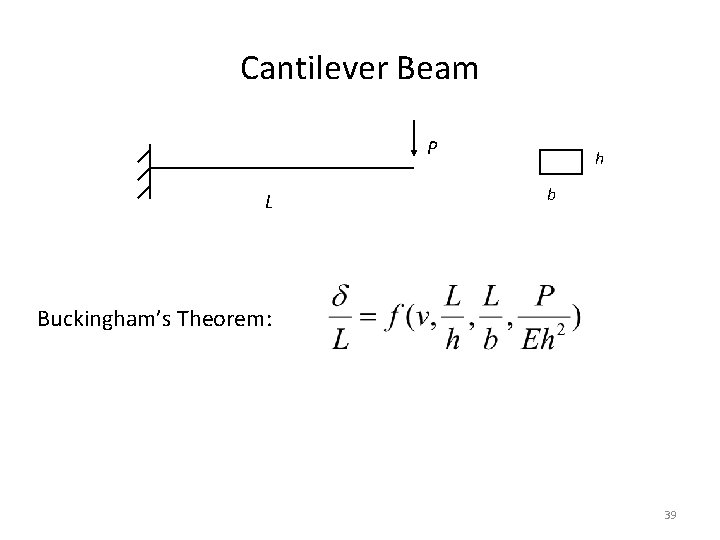
Cantilever Beam P L h b Buckingham’s Theorem: 39

Fracture Mechanics Propose: Rayleigh’s Procedure: for dimensional consistency 40

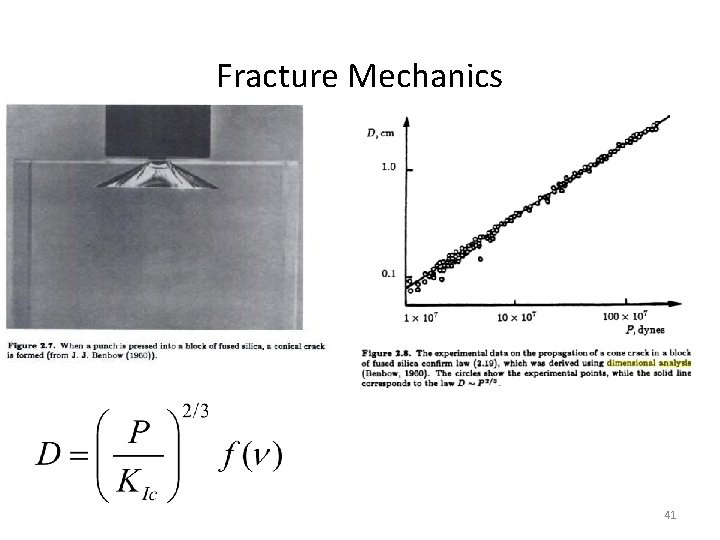
Fracture Mechanics 41

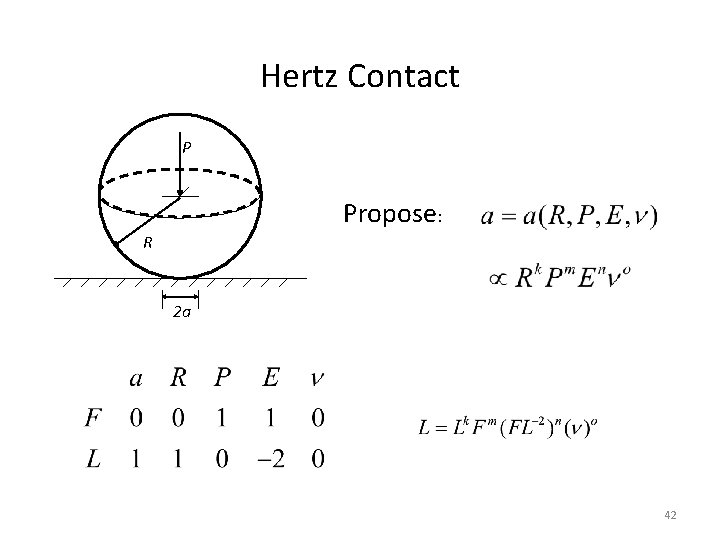
Hertz Contact P Propose: R 2 a 42

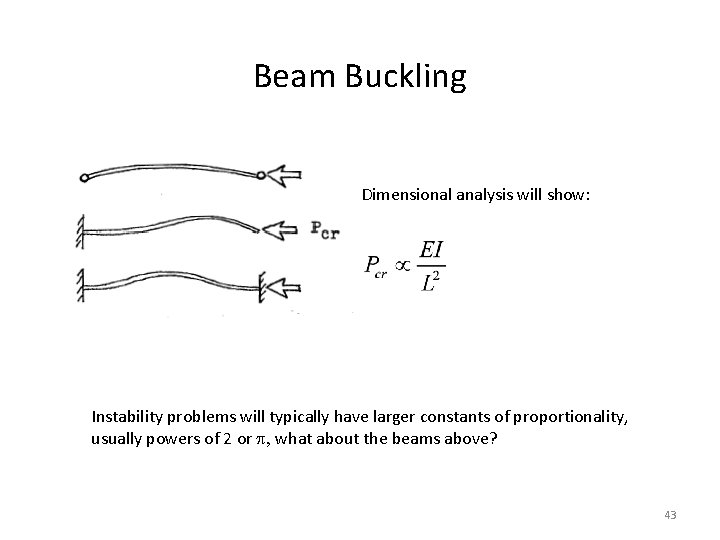
Beam Buckling Dimensional analysis will show: Instability problems will typically have larger constants of proportionality, usually powers of 2 or p, what about the beams above? 43

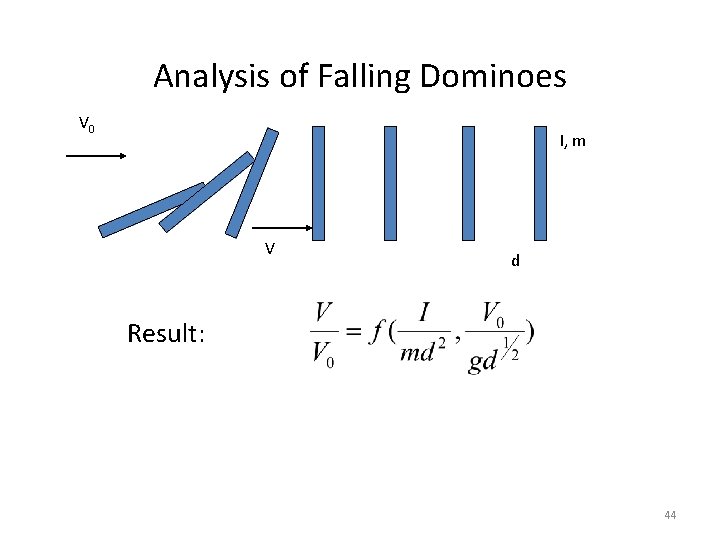
Analysis of Falling Dominoes V 0 I, m V d Result: 44

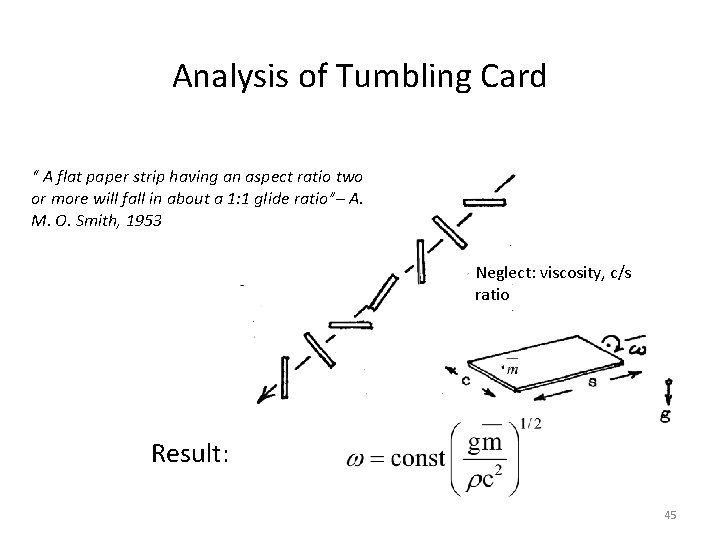
Analysis of Tumbling Card “ A flat paper strip having an aspect ratio two or more will fall in about a 1: 1 glide ratio”– A. M. O. Smith, 1953 Neglect: viscosity, c/s ratio Result: 45

Analysis of Tumbling Card 46

Dead Man’s Dive The dive coach claims that a man who holds himself rigid as he topples from a 3 -meter diving board will execute a successful dive. How is this result changed for a small boy? 47

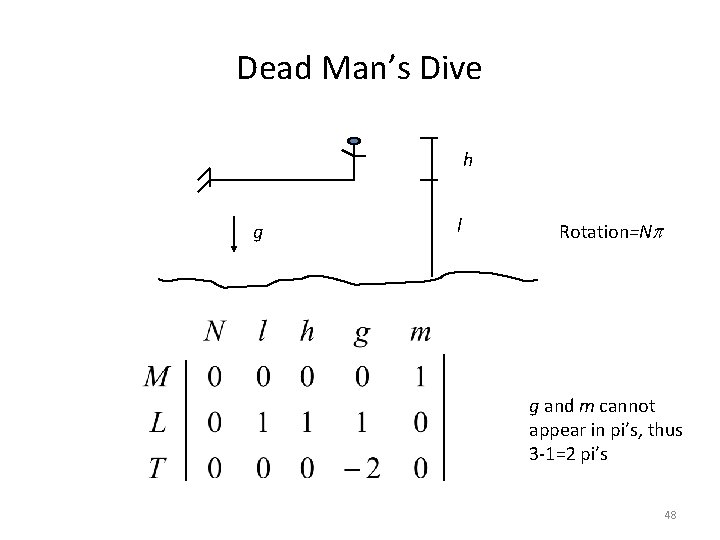
Dead Man’s Dive h g l Rotation=Np g and m cannot appear in pi’s, thus 3 -1=2 pi’s 48

Dead Man’s Dive h g l Rotation=Np • Thus, for the small boy to make a perfect dive, the board height must be reduced • Coach says for N=1, h/l=0. 6, i. e for l=3 m, h=5 ft-10 in. 49

Dead Man’s Dive h g l Rotation=q= Np • Rigid body dynamics analysis- pivot then free fall 7 ft, 6 in man executes perfect dive, mass distribution off 50

Analysis of Rowing Records Mc. Mahon (1979) has shown that, using dimensional analysis, that the speed of a racing shell varies as the 1/9 power of the number of oarsmen. This is in excellent agreement with championship times for 1, 2, 4, and 8 man boats. Show this assuming the following: all boats and their positions in the water are geometrically similar, the boat weight per oarsmen wb is constant, each oarsman contributes power Po and weight wo, the only drag is due to skin friction, which is proportional to the wetted area and the square of the speed 51

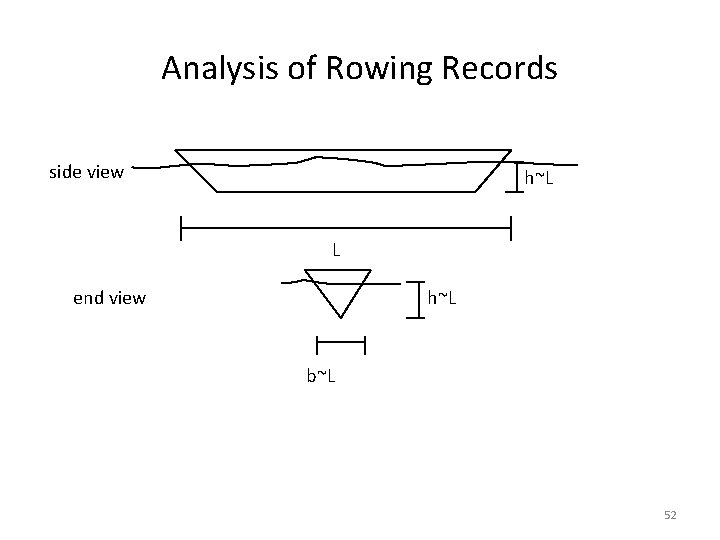
Analysis of Rowing Records side view h~L L end view h~L b~L 52

Analysis of Rowing Records Archimedes's Principle Energy Balance 53

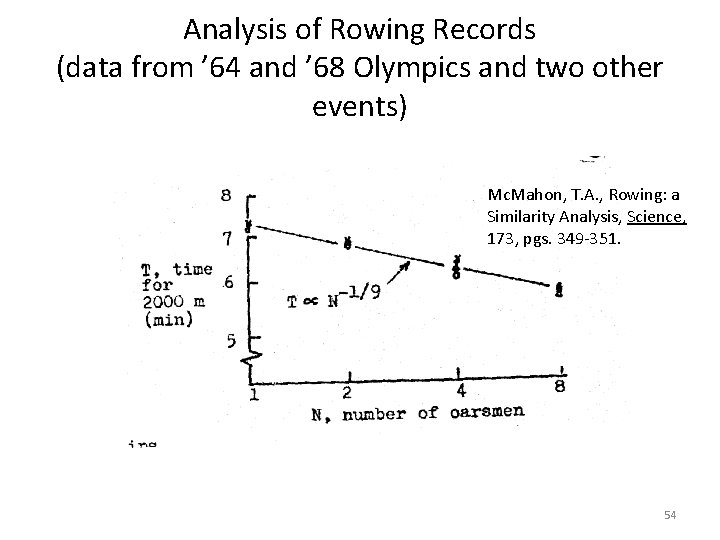
Analysis of Rowing Records (data from ’ 64 and ’ 68 Olympics and two other events) Mc. Mahon, T. A. , Rowing: a Similarity Analysis, Science, 173, pgs. 349 -351. 54

Splattering Raindrop When a drop of ink strikes a piece of paper at sufficiently low speed, surface tension keeps it round, so it makes a circular spot. As the impact speed is increased, dynamic forces overcome the smoothing effect of surface tension, the splattering drop becomes unstable, and it forms a spiked star shape. 55

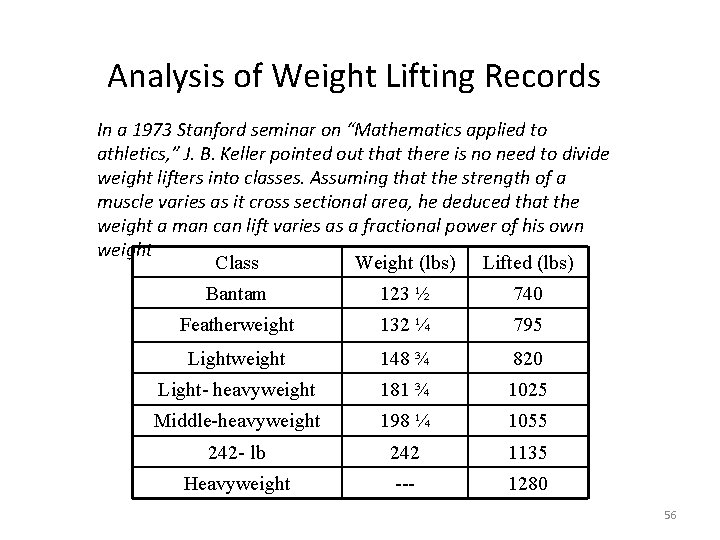
Analysis of Weight Lifting Records In a 1973 Stanford seminar on “Mathematics applied to athletics, ” J. B. Keller pointed out that there is no need to divide weight lifters into classes. Assuming that the strength of a muscle varies as it cross sectional area, he deduced that the weight a man can lift varies as a fractional power of his own weight Class Weight (lbs) Lifted (lbs) Bantam 123 ½ 740 Featherweight 132 ¼ 795 Lightweight 148 ¾ 820 Light- heavyweight 181 ¾ 1025 Middle-heavyweight 198 ¼ 1055 242 - lb 242 1135 Heavyweight --- 1280 56

Analysis of Weight Lifting Records A H 57

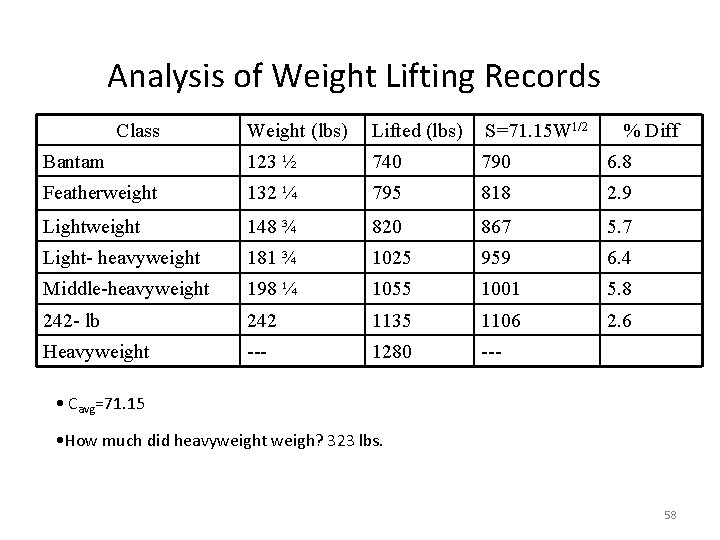
Analysis of Weight Lifting Records Class Weight (lbs) Lifted (lbs) S=71. 15 W 1/2 % Diff Bantam 123 ½ 740 790 6. 8 Featherweight 132 ¼ 795 818 2. 9 Lightweight 148 ¾ 820 867 5. 7 Light- heavyweight 181 ¾ 1025 959 6. 4 Middle-heavyweight 198 ¼ 1055 1001 5. 8 242 - lb 242 1135 1106 2. 6 Heavyweight --- 1280 --- • Cavg=71. 15 • How much did heavyweight weigh? 323 lbs. 58

Nondimensionalization of the NSE • We define nondimensional variables, using the scaling parameters in Table 10 -1 • To plug the nondimensional variables into the NSE, we need to first rearrange the equations in terms of the dimensional variables

Nondimensionalization of the NSE • Now we substitute into the NSE to obtain • Every additive term has primary dimensions {m 1 L-2 t-2}. To nondimensionalize, we multiply every term by L/( V 2), which has primary dimensions {m-1 L 2 t 2}, so that the dimensions cancel. After rearrangement,

Nondimensionalization of the NSE • Terms in [ ] are nondimensional parameters Strouhal number Euler number Inverse of Froude number squared Navier-Stokes equation in nondimensional form Inverse of Reynolds number

Nondimensionalization of the NSE • Nondimensionalization vs. Normalization – NSE are now nondimensional, but not necessarily normalized. What is the difference? – Nondimensionalization concerns only the dimensions of the equation we can use any value of scaling parameters L, V, etc. – Normalization is more restrictive than nondimensionalization. To normalize the equation, we must choose scaling parameters L, V, etc. that are appropriate for the flow being analyzed, such that all nondimensional variables are of order of magnitude unity, i. e. , their minimum and maximum values are close to 1. 0. If we have properly normalized the NSE, we can compare the relative importance of the terms in the equation by comparing the relative magnitudes of the nondimensional parameters St, Eu, Fr, and Re.

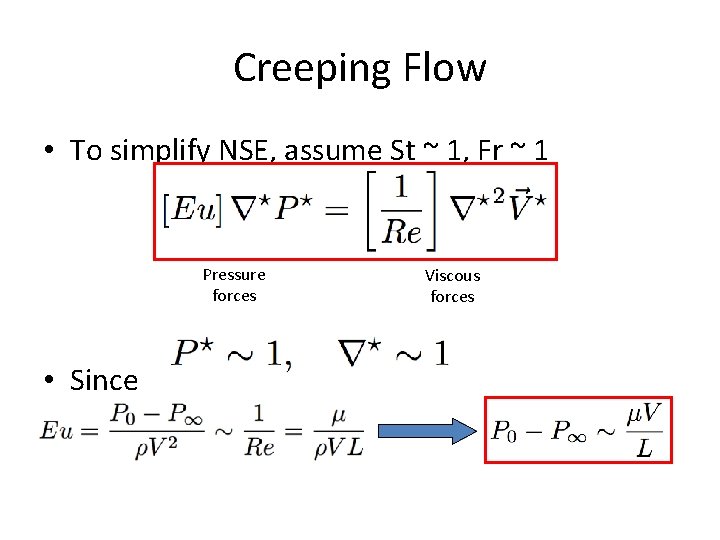
Creeping Flow • To simplify NSE, assume St ~ 1, Fr ~ 1 Pressure forces • Since Viscous forces

Creeping Flow • This is important – Very different from inertia dominated flows where – Density has completely dropped out of NSE. To demonstrate this, convert back to dimensional form. – This is now a LINEAR EQUATION which can be solved for simple geometries.

Creeping Flow • Solution of Stokes flow is beyond the scope of this course. • Analytical solution for flow over a sphere gives a drag coefficient which is a linear function of velocity V and viscosity m.