AK Softwaretechnologie Geometric Kernel Computational Geometry Algorithms Library

AK Softwaretechnologie Geometric Kernel Computational Geometry Algorithms Library Klaus Schuch 9831011

Inhalt • • • Motivation Ziele und Forderungen Eigenschaften anderer Bibliotheken Struktur des CGAL Kernels Funktoren Design eines vereinfachten Kernels Vordefinierte CGAL Kernels Exakte Berechnungen (Filter) Traits Klassen d-dimensionaler Kernel

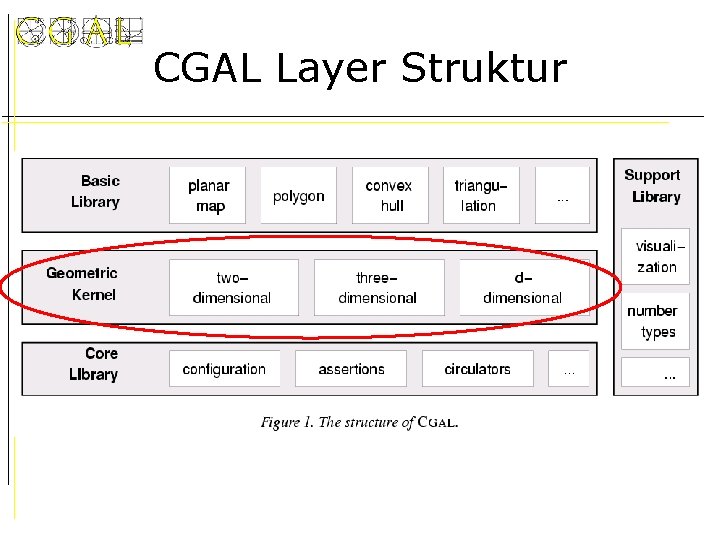
CGAL Layer Struktur

Motivation • Geometrische Algorithmen auf Objekte werden im Normalfall unabhängig von deren Repräsentation beschrieben. • Verwendung von Operationen und Prädikaten => einfachere Beschreibung

Ziel • Kapselung der Repräsentation in einem Kernel • Algorithmen arbeiten NUR mit den vom Kernel zur Verfügung gestellten Operationen => Repräsentationsunabhängige affine Geometrie

Forderungen • • Exaktheit Robustheit Effizienz Flexibilität – Adaptierbarkeit – Erweiterbarkeit => Generisches Programmieren

Andere Bibliotheken • PLAGEO/SPAGEO (C++): – 2 d und 3 d Objekte – Klassenhierarchie, gemeinsame Basisklasse • LEDA (C++): – Exact rational arithmetic Kernel – Floating point arithmetic Kernel • Geom. Lib (Java): – Klassenhierarchie – Java Interfaces

Kernel Architektur • Kernel besteht aus: – Typen für geometrische Objekte konstanter Größe (Punkt, Vektor, Linie, Kreis, …) – Operationen auf diese Typen • Prädikate • Konstruktoren • Für jede Operation: – Globale Funktion oder Member-Function – Function Object

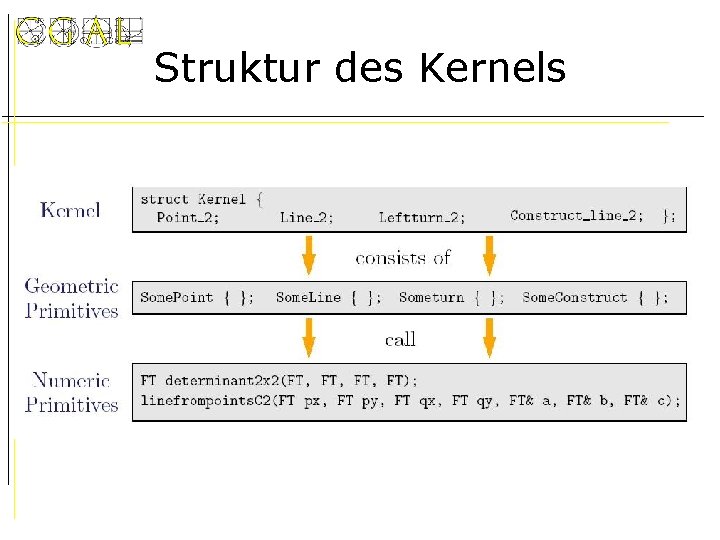
Struktur des Kernels

Funktoren (Function Objects) (1) • Funktionen anpassbar machen – Funktionszeiger („C Stil“) – Virtuelle Funktionen („Java Stil“) – Funktoren („STL Stil“)

Funktoren (Function Objects) (2) • Abstraktion einer Funktion • Klassen mit operator() • Vorteile: – Effizenz (Klassendefinition zur Compile-Zeit bekannt -> inline möglich) – Zustand speicherbar

Beispiel K k; K: : Construct_line_2 c_line = k. construct_line_2_object(); K: : Less_xy_2 less_xy = k. less_xy_2_object(); K: : Point_2 p(0, 1); K: : Point_2 q(1, -4); K: : Line_2 line = c_line(p, q); if (less_xy(p, q)) {. . . }

Vereinfachter Kernel (1) Construct_line_2 muß Point_2 und Line_2 kennen Kernel als Template-Parameter bei Klassen für geometrische Objekte: template < class K > struct My. Point {. . . }; template < class K > struct My. Line {. . . }; template < class K > struct My. Construct {. . . }; struct Kernel { typedef My. Point< Kernel > Point_2; typedef My. Line< Kernel > Line_2; typedef My. Construct< Kernel > Construct_line_2; };

Vereinfachter Kernel (2) • Erweiterung des Kernels: struct New_kernel : public Kernel { typedef New. Point<New_kernel> Point_2; typedef My. Left. Turn<New_kernel> Left_turn_2; }; Problem: My. Line, My. Construct sind noch mit Kernel parametrisiert!

Vereinfachter Kernel (3) • Triviale Lösung: My. Line, My. Construct in New_Kernel erneut definieren • Bessere Lösung: – Parametrisierung nicht sofort fixieren – „instantiation engine“ verwenden template < class K > struct Kernel_base { typedef My. Point< K > Point_2; typedef My. Line< K > Line_2; typedef My. Construct< K > Construct_line_2; }; struct Kernel : public Kernel_base< Kernel > {};

Vereinfachter Kernel (4) • Erweiterung des Kernels: template < class K > struct New_kernel_base : public Kernel_base< K > { typedef New. Point< K > Point_2; typedef My. Left. Turn< K > Left_turn_2; }; struct New_kernel : public New_kernel_base<New_kernel> {}; • Keine Laufzeitverschlechterung!

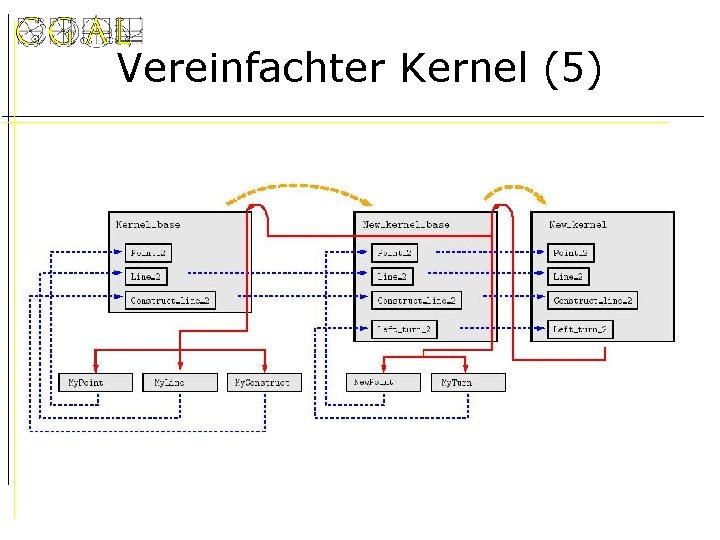
Vereinfachter Kernel (5)

CGAL Kernels mit Reference Counting • Cartesian< Field. Type > • Homogeneous< Ring. Type > Ohne Reference Counting • Simple_cartesian< Field. Type > • Simple_homogeneous< Ring. Type > Vordefinierte Kernels • Exact_predicates_exact_constructions_kernel_with_sqrt – benötigt LEDA oder CORE • Exact_predicates_inexact_constructions_kernel

Exakte Berechnungen • Exakte numerische Typen – z. B. Quotient<MP_float>, leda_real, • Filter (bei Prädikaten) – Berechnung mit schnellen floating-point Typen durchführen – Wenn Fehler zu groß (Exception), dann Berechnung mit exakten Typen wiederhole

Filter (1) • Beispiel - Left_turn_2 Prädikat – durch 3 x 3 Determinate berechenbar – Koordinaten der Punkte im Intervall (-1, 1) – Ok, wenn Absolut-Wert > 2, 66*10 -15 • Filter in CGAL – Filtered_Kernel< CK > – Filtered_predicate< … >

CGAL Number Types • • • Quotient < NT > MP_Float Lazy_exact_nt < NT > Fixed_precision_nt Interval_nt, Interval_nt_advanced

Filter (2) typedef CGAL: : Simple_cartesian<double> CK; typedef CGAL: : Filtered_kernel<CK> Filtered_K; typedef CGAL: : Simple_cartesian<double> K; typedef CGAL: : Simple_cartesian<CGAL: : Interval_nt_advanced> FK; typedef CGAL: : Simple_cartesian<CGAL: : MP_Float> EK; typedef CGAL: : Cartesian_converter<K, EK> C 2 E; typedef CGAL: : Cartesian_converter<K, FK> C 2 F; typedef CGAL: : Filtered_predicate<EK: : Orientation_2, FK: : Orientation_2, C 2 E, C 2 F> Orientation_2; int main() { K: : Point_2 p(1, 2), q(2, 3), r(3, 4); Orientation_2 orientation; CGAL: : Orientation o = orientation(p, q, r); return 0; }

Traits Klassen (1) • Klasse die „nützliche“ Typen und Operationen zusammenfasst • Traits-Klasse definiert die Schnittstelle zwischen Algorithmen und den geometrischen Objekten • Kernel kann meist als Traits Klasse verwendet werden.

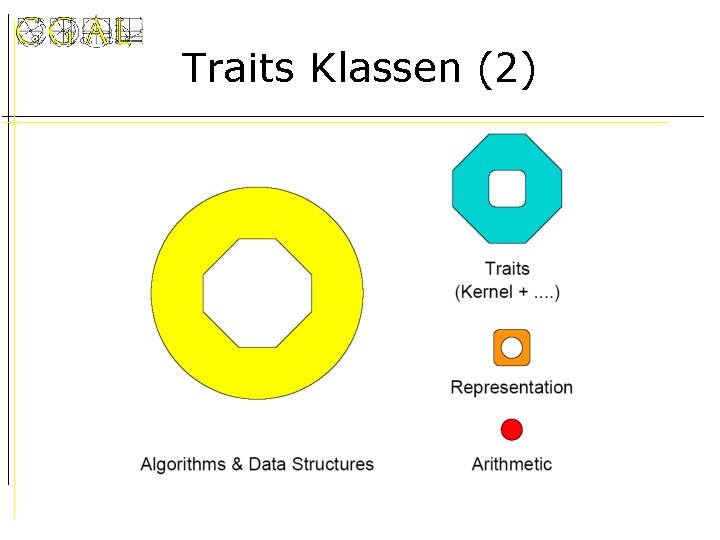
Traits Klassen (2)

Traits Klassen (3) template <class Input. Iterator, class Output. Iterator, class Traits> Output. Iterator ch_graham_andrew( Input. Iterator first, Input. Iterator beyond, Output. Iterator result, Traits ch_traits) {. . . } • arbeitet mit Objekten vom Typ Traits: : Point_2 • verwendet die Prädikate Traits: : Leftturn_2 und Traits: : Less_xy_2

d-dimensionaler Kernel • Zusätzlicher Parameter Linear. Algebra - Concept – Cartesian_d<Field. Type, Linear. Algebra> – Homogeneous_d<Field. Type, Linear. Algebra> • Dieser Parameter ist nicht zwingend erforderlich!