AIRTHMETIC MEAN VIDUAL SERIES DIRECT METHOD DISCRETE SERIES







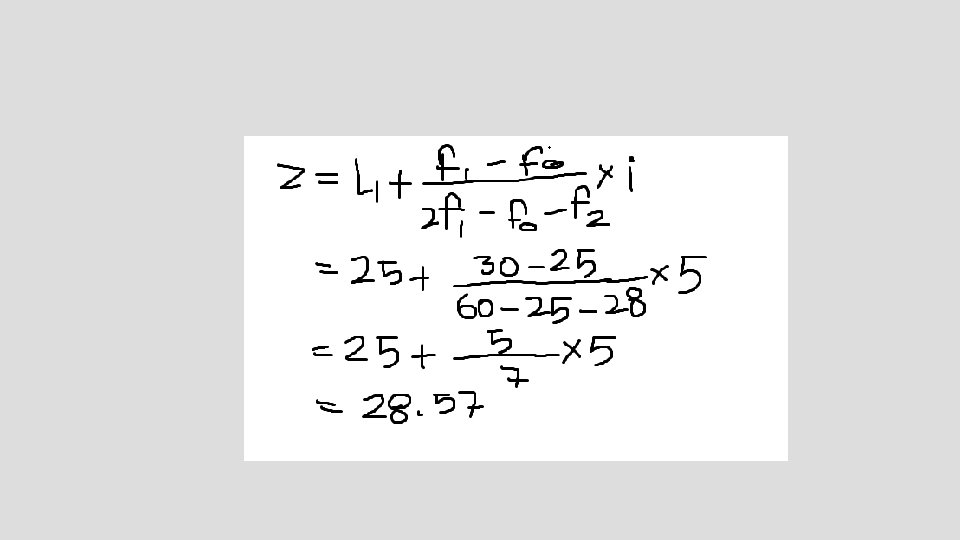
- Slides: 24

AIRTHMETIC MEAN VIDUAL SERIES DIRECT METHOD DISCRETE SERIES 1. DIRECT METHOD X= CONTINUOUS SERIES OR F REQUENCY DISTRIBUTION 1. DIRECT METHOD HORT CUT METHOD 2. SHORT CUT METHOD A+ X = A+ X= fd f X–A ASSUMED MEAN 3. STEP DEVIATION METHOD X = A+ fd’ x. C f 3. STEPDEVIATION METHOD.

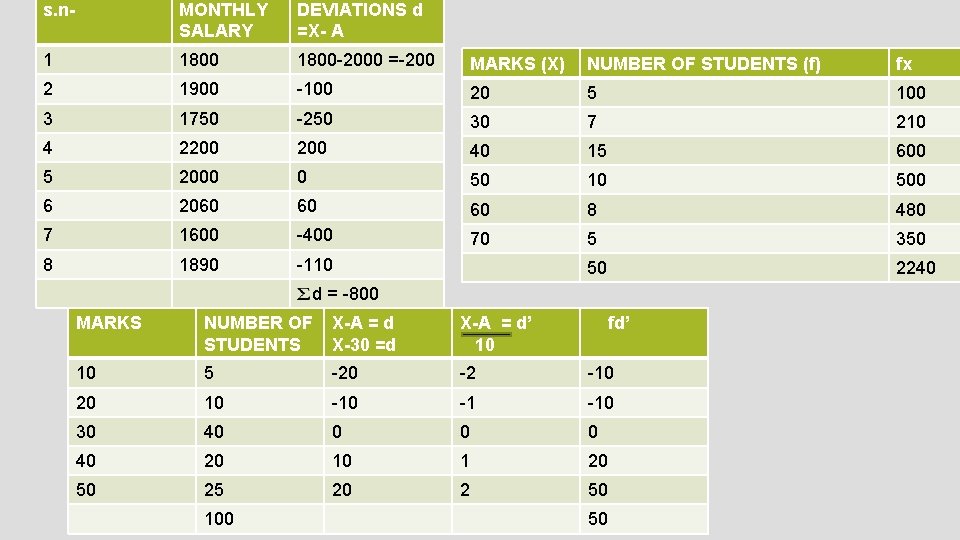
s. n- MONTHLY SALARY DEVIATIONS d =X- A 1 1800 -2000 =-200 MARKS (X) NUMBER OF STUDENTS (f) fx 2 1900 -100 20 5 100 3 1750 -250 30 7 210 4 2200 40 15 600 5 2000 0 50 10 500 6 2060 60 60 8 480 7 1600 -400 70 5 350 8 1890 -110 50 2240 d = -800 MARKS NUMBER OF STUDENTS X-A = d X-30 =d X-A = d’ 10 10 5 -20 -2 -10 20 10 -1 -10 30 40 20 10 1 20 50 25 20 2 50 100 fd’ 50


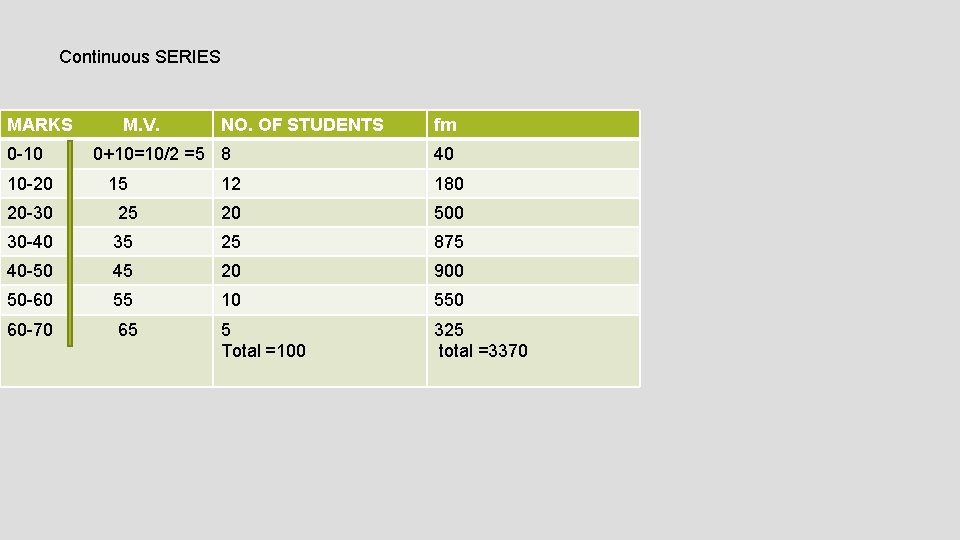
Continuous SERIES MARKS 0 -10 10 -20 M. V. NO. OF STUDENTS 0+10=10/2 =5 8 15 fm 40 12 180 20 -30 25 20 500 30 -40 35 25 875 40 -50 45 20 900 50 -60 55 10 550 60 -70 65 5 Total =100 325 total =3370

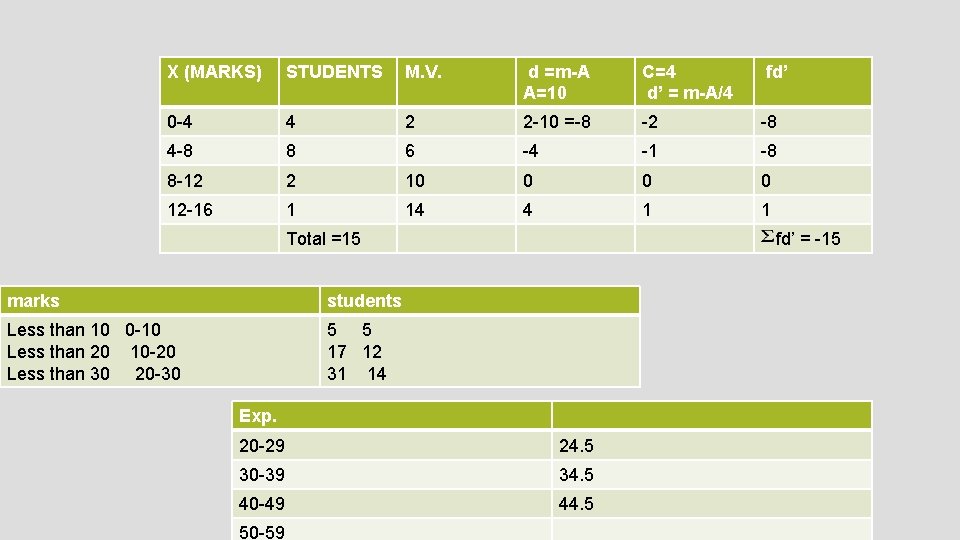
X (MARKS) STUDENTS M. V. d =m-A A=10 C=4 d’ = m-A/4 fd’ 0 -4 4 2 2 -10 =-8 -2 -8 4 -8 8 6 -4 -1 -8 8 -12 2 10 0 12 -16 1 14 4 1 1 Total =15 marks students Less than 10 0 -10 Less than 20 10 -20 Less than 30 20 -30 5 5 17 12 31 14 fd’ = -15 Exp. 20 -29 24. 5 30 -39 34. 5 40 -49 44. 5 50 -59

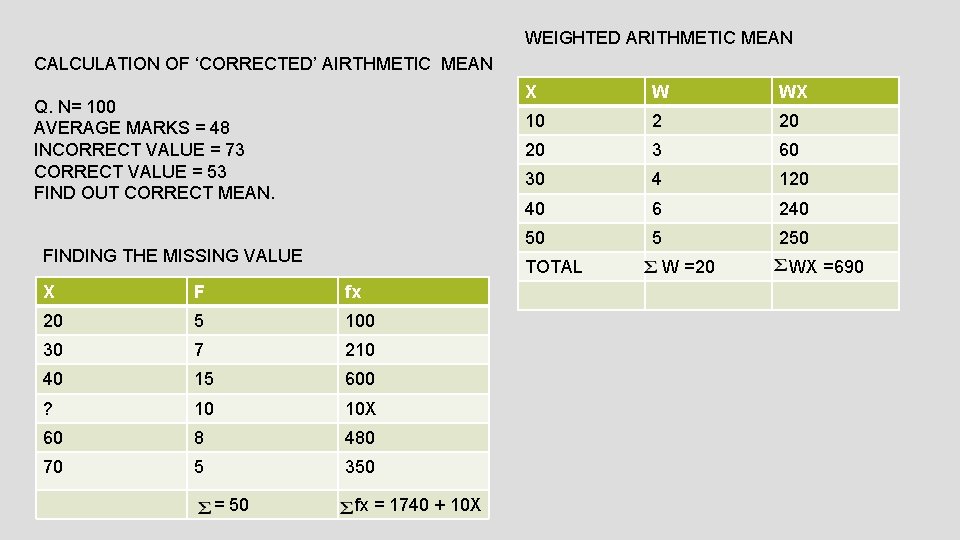
WEIGHTED ARITHMETIC MEAN CALCULATION OF ‘CORRECTED’ AIRTHMETIC MEAN Q. N= 100 AVERAGE MARKS = 48 INCORRECT VALUE = 73 CORRECT VALUE = 53 FIND OUT CORRECT MEAN. FINDING THE MISSING VALUE W WX 10 2 20 20 3 60 30 4 120 40 6 240 50 5 250 TOTAL X F fx 20 5 100 30 7 210 40 15 600 ? 10 10 X 60 8 480 70 5 350 = 50 X fx = 1740 + 10 X W =20 WX =690

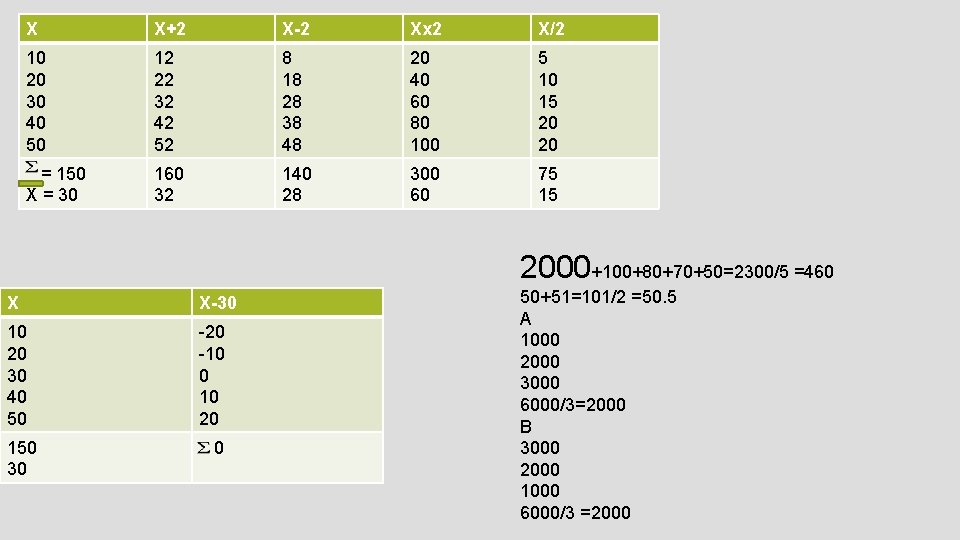
X X+2 X-2 Xx 2 X/2 10 20 30 40 50 12 22 32 42 52 8 18 28 38 48 20 40 60 80 100 5 10 15 20 20 = 150 X = 30 160 32 140 28 300 60 75 15 2000+100+80+70+50=2300/5 =460 X X-30 10 20 30 40 50 -20 -10 0 10 20 150 30 0 50+51=101/2 =50. 5 A 1000 2000 3000 6000/3=2000 B 3000 2000 1000 6000/3 =2000

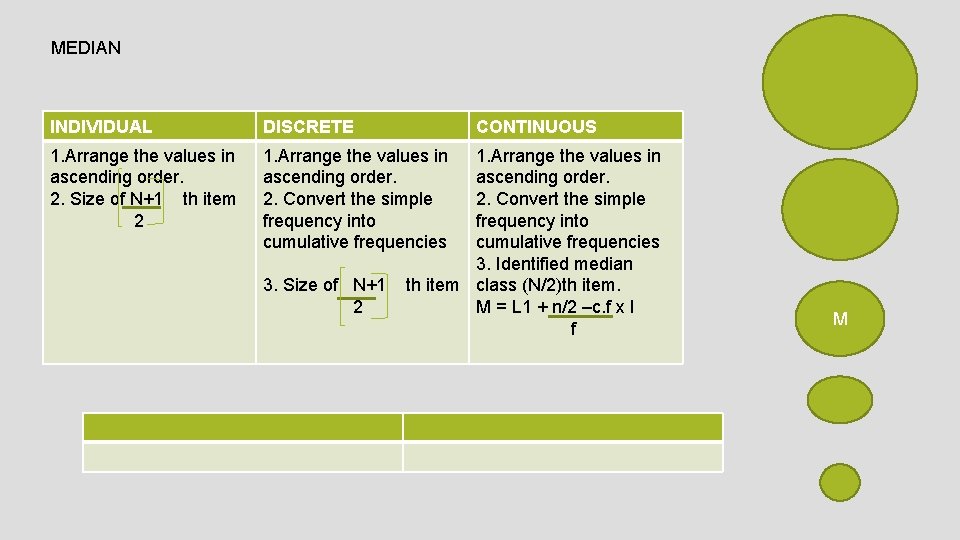
MEDIAN INDIVIDUAL DISCRETE 1. Arrange the values in ascending order. 2. Size of N+1 th item 2 1. Arrange the values in ascending order. 2. Convert the simple frequency into cumulative frequencies 3. Size of N+1 2 CONTINUOUS 1. Arrange the values in ascending order. 2. Convert the simple frequency into cumulative frequencies 3. Identified median th item class (N/2)th item. M = L 1 + n/2 –c. f x I f M

S. NO. X X 1. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 17 32 35 33 15 21 41 32 11 18 20 22 11 15 35 23 38 12 11. 11 12 15 15 17 18 20 21 22 23 32 32 33 35 35 38 41 SIZE OF 18+1=19/2 = 9. 5 TH ITEM 21+22= 43/2 = 21. 5 M = 21. 5

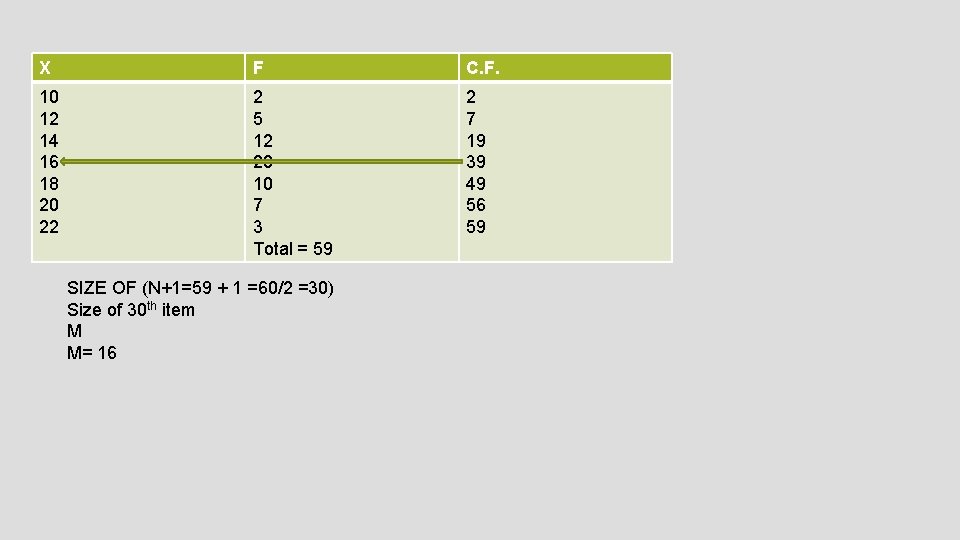
X F C. F. 10 12 14 16 18 20 22 2 5 12 20 10 7 3 Total = 59 2 7 19 39 49 56 59 SIZE OF (N+1=59 + 1 =60/2 =30) Size of 30 th item M M= 16

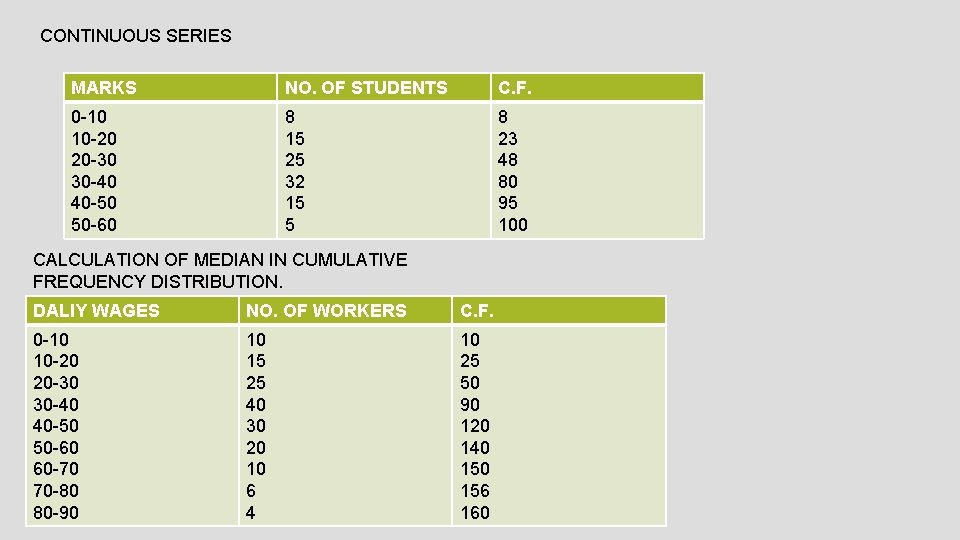
CONTINUOUS SERIES MARKS NO. OF STUDENTS C. F. 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 8 15 25 32 15 5 8 23 48 80 95 100 CALCULATION OF MEDIAN IN CUMULATIVE FREQUENCY DISTRIBUTION. DALIY WAGES NO. OF WORKERS C. F. 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 60 -70 70 -80 80 -90 10 15 25 40 30 20 10 6 4 10 25 50 90 120 140 156 160

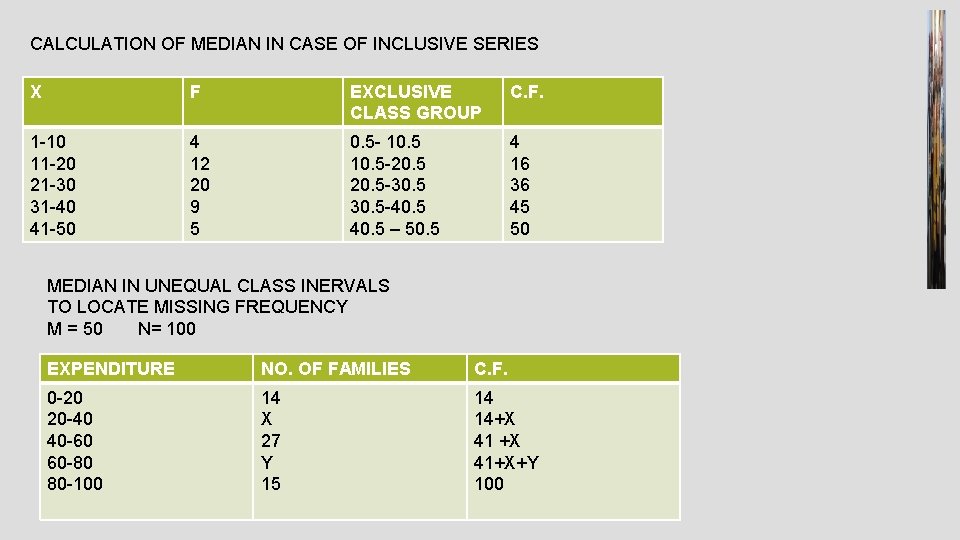
CALCULATION OF MEDIAN IN CASE OF INCLUSIVE SERIES X F EXCLUSIVE CLASS GROUP C. F. 1 -10 11 -20 21 -30 31 -40 41 -50 4 12 20 9 5 0. 5 - 10. 5 -20. 5 -30. 5 -40. 5 – 50. 5 4 16 36 45 50 MEDIAN IN UNEQUAL CLASS INERVALS TO LOCATE MISSING FREQUENCY M = 50 N= 100 EXPENDITURE NO. OF FAMILIES C. F. 0 -20 20 -40 40 -60 60 -80 80 -100 14 X 27 Y 15 14 14+X 41+X+Y 100

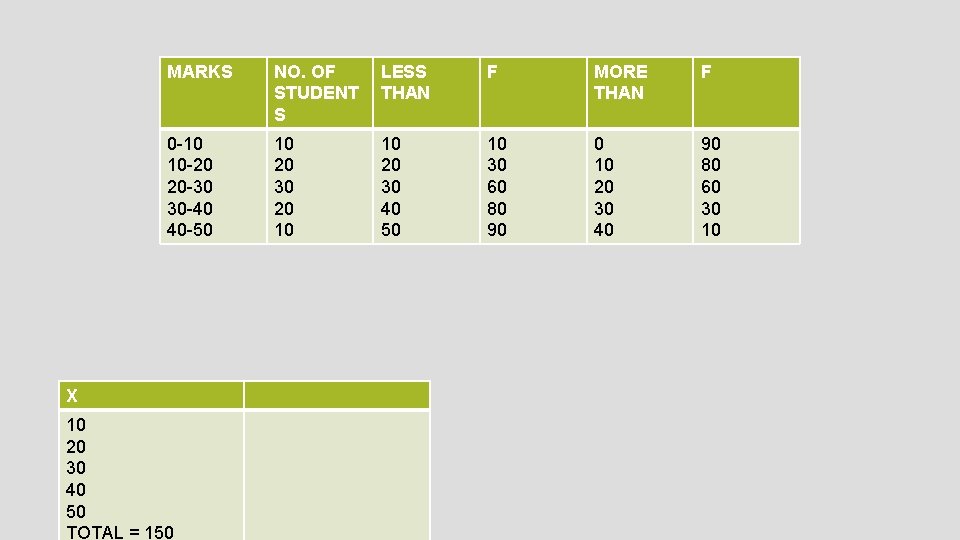
MARKS NO. OF STUDENT S LESS THAN F MORE THAN F 0 -10 10 -20 20 -30 30 -40 40 -50 10 20 30 20 10 10 20 30 40 50 10 30 60 80 90 0 10 20 30 40 90 80 60 30 10 X 10 20 30 40 50 TOTAL = 150

Merits and Demerits of median. MERITS : 1. SIMPLICITY 2. FREE FROM EFFECT OF EXTREME VALUES 3. CERTAINTY 4. REAL VALUE 5. GRAPHIC PRESENTATION 6. POSSIBLE EVEN WHEN DATA IS INCOMPLETE DEMERITS 1. LACK OF REPRESENTIVE CHARACTER 2. UNREALISTIC 3. LACK OF ALGEBRAIC TREATMENT

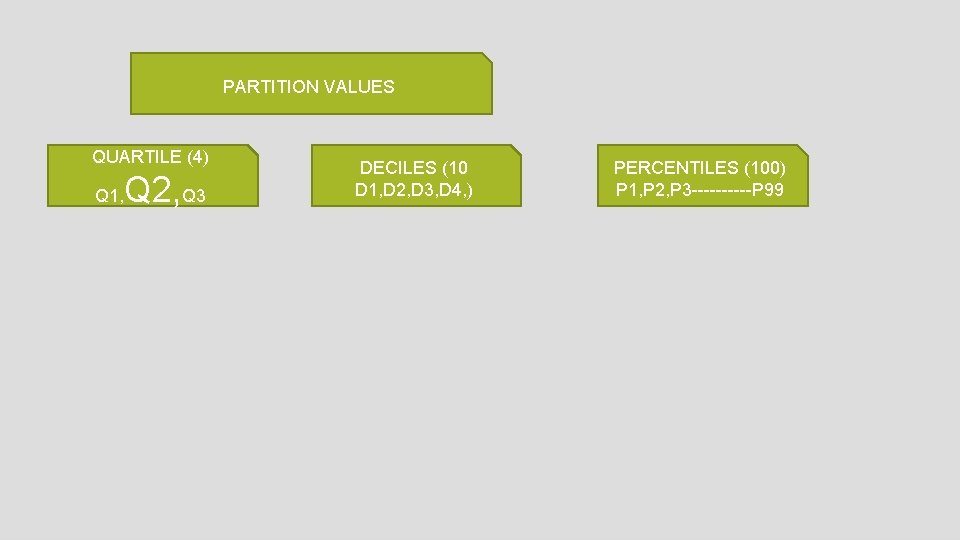
PARTITION VALUES QUARTILE (4) Q 1, Q 2, Q 3 DECILES (10 D 1, D 2, D 3, D 4, ) PERCENTILES (100) P 1, P 2, P 3 -----P 99

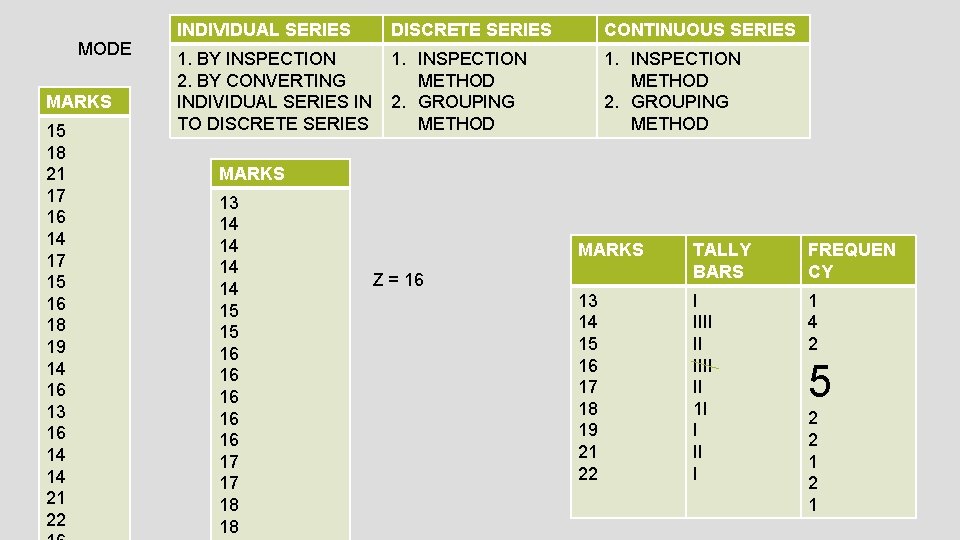
MODE MARKS 15 18 21 17 16 14 17 15 16 18 19 14 16 13 16 14 14 21 22 INDIVIDUAL SERIES DISCRETE SERIES CONTINUOUS SERIES 1. BY INSPECTION 2. BY CONVERTING INDIVIDUAL SERIES IN TO DISCRETE SERIES 1. INSPECTION METHOD 2. GROUPING METHOD MARKS 13 14 14 15 15 16 16 16 17 17 18 18 MARKS TALLY BARS FREQUEN CY 13 14 15 16 17 18 19 21 22 I IIII II 1 I I II I 1 4 2 Z = 16 5 2 2 1

DISCRETE SERIES MONTHLY SALARY NO. OF WORKERS 1000 1200 1400 1600 1800 2000 2200 Z =1600 7 10 14 26 10 5 3

GROUPING METHOD X 10 11 12 13 14 15 16 17 18 F 3 10 20 24 25 11 10 8 2 GROUPING TABLE X F (COLUM N I) 10 11 12 13 14 15 16 17 18 3 10 20 24 25 11 10 8 2 II 13 III IV 30 V VI 33 54 44 49 69 60 36 21 46 29 18 10 20

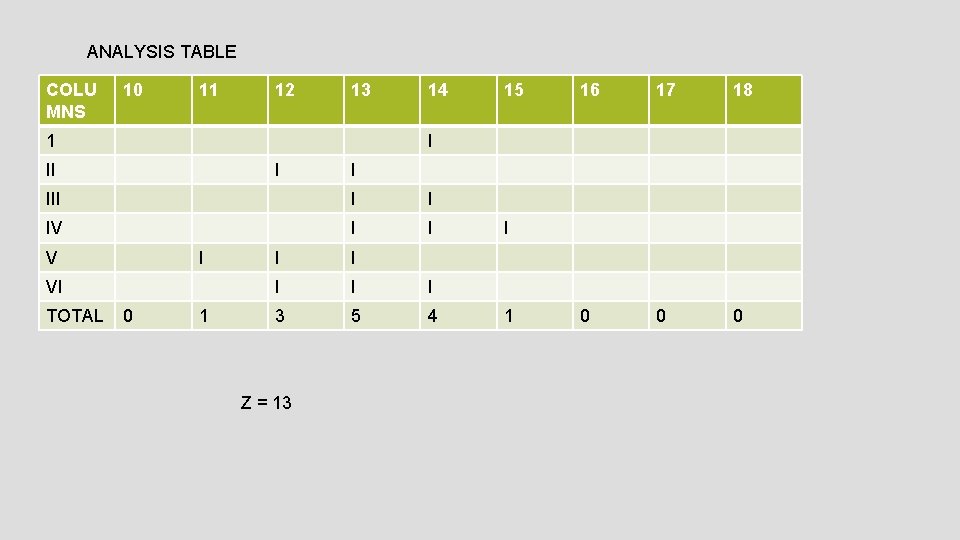
ANALYSIS TABLE COLU MNS 10 11 12 13 1 14 16 17 18 0 0 0 I II I I IV I I VI TOTAL 15 0 1 I I I 3 5 4 Z = 13 I 1

L 1=30 I = 10 MODE IN CONTINUOUS SERIES INSPECTION METHOD X 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 60 -70 70 -80 Y 4 12 18 f 0 25 f 1 16 f 2 9 7 3

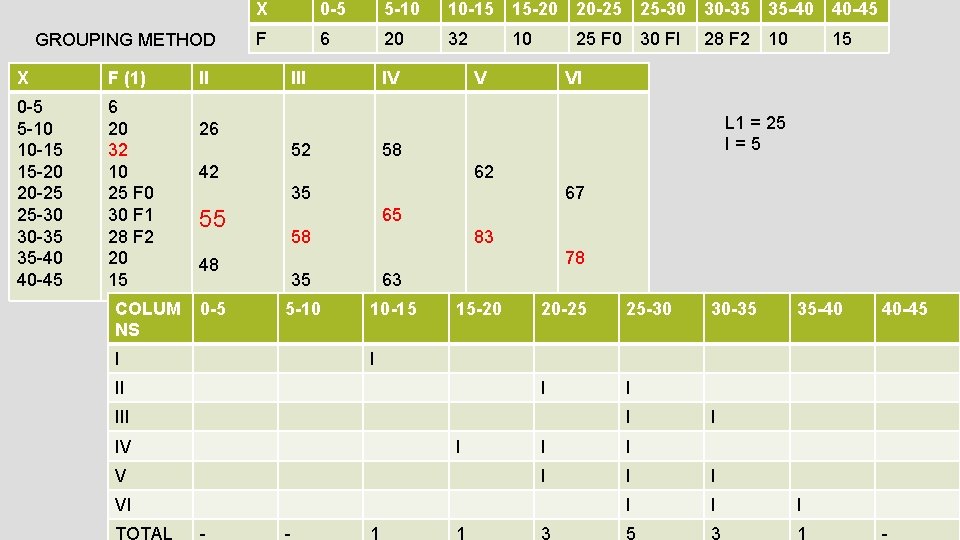
GROUPING METHOD X F (1) 0 -5 5 -10 10 -15 15 -20 20 -25 25 -30 30 -35 35 -40 40 -45 6 20 32 10 25 F 0 30 F 1 28 F 2 20 15 COLUM NS I II X 0 -5 5 -10 10 -15 15 -20 20 -25 25 -30 30 -35 35 -40 40 -45 F 6 20 32 III IV 10 25 F 0 V 52 58 62 67 35 48 0 -5 VI 15 L 1 = 25 I=5 42 55 10 VI 65 83 58 78 35 63 5 -10 10 -15 15 -20 20 -25 25 -30 I I 30 -35 35 -40 I III V 28 F 2 26 II IV 30 FI I I 40 -45
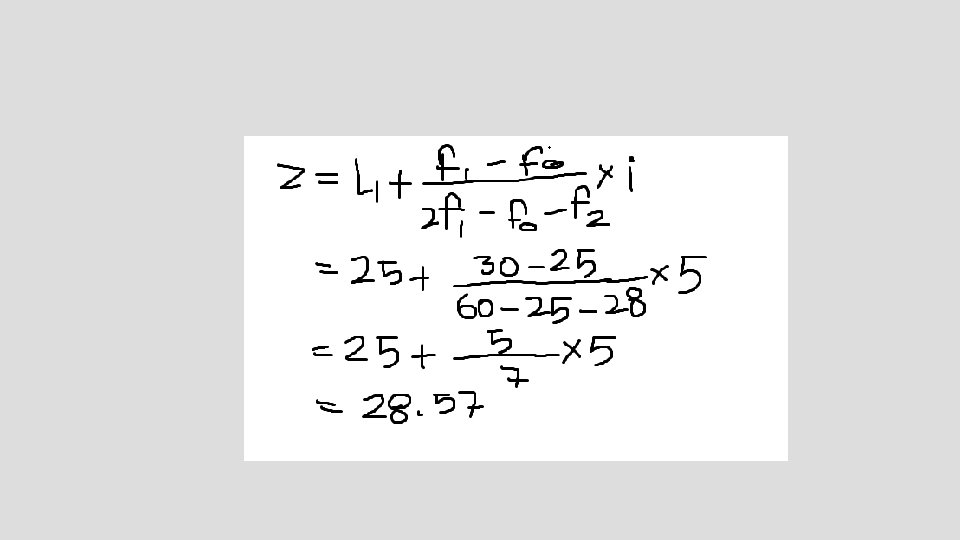

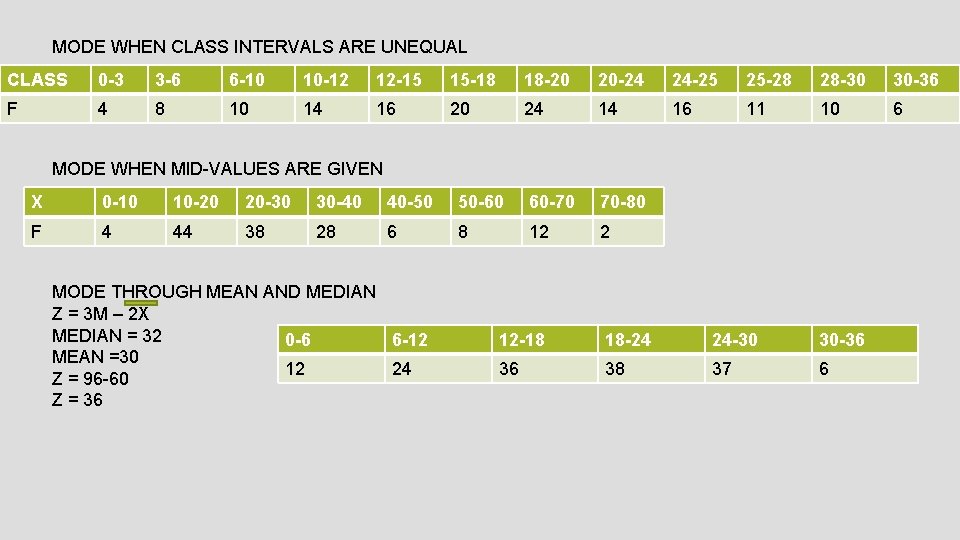
MODE WHEN CLASS INTERVALS ARE UNEQUAL CLASS 0 -3 3 -6 6 -10 10 -12 12 -15 15 -18 18 -20 20 -24 24 -25 25 -28 28 -30 30 -36 F 4 8 10 14 16 20 24 14 16 11 10 6 MODE WHEN MID-VALUES ARE GIVEN X 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 60 -70 70 -80 F 4 44 38 28 6 8 12 2 MODE THROUGH MEAN AND MEDIAN Z = 3 M – 2 X MEDIAN = 32 0 -6 6 -12 MEAN =30 12 24 Z = 96 -60 Z = 36 12 -18 18 -24 24 -30 30 -36 36 38 37 6

GRAPHIC LOCATION OF MODE X 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 60 -70 F 5 10 20 25 20 10 5 25 20 15 10 5 0 I 0 20 Z = 35 30 4 0 5 0 60 70