Aircraft Structures Chapter 19 Combined open and closed

Aircraft Structures Chapter 19 - Combined open and closed section beams

Introduction • Frequently, aircraft components comprise combinations of open and closed section beams. Fig. 19. 1: the section of a wing in the region of an undercarriage bay. Part of the section is an open channel section, while the nose is a single-cell closed section.

19. 1 Bending • It is immaterial what form the cross-section takes; the direct stresses due to bending are given by either of the below equations: r e b m e R this from ! 6 1 r e t p a ch
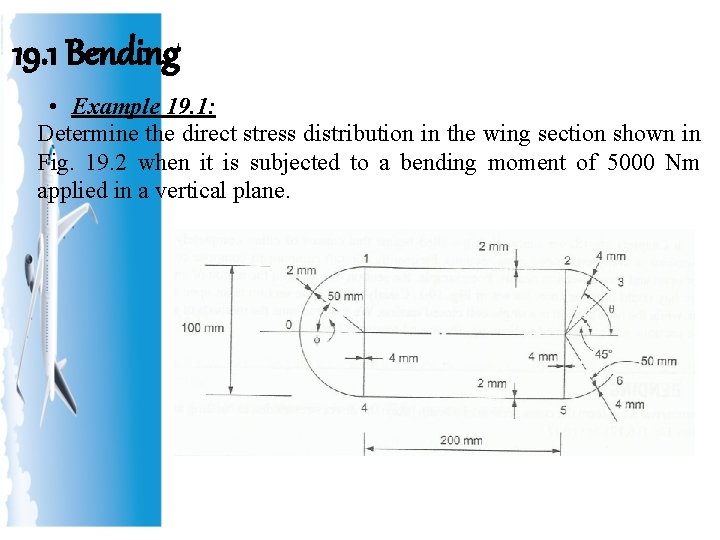
19. 1 Bending • Example 19. 1: Determine the direct stress distribution in the wing section shown in Fig. 19. 2 when it is subjected to a bending moment of 5000 Nm applied in a vertical plane.

19. 1 Bending • Example 19. 1: (cont’d) The beam section has the x axis as an axis of symmetry so that Ixy= 0 and, also, since My=0 Eq. (16. 18) reduces to From section 16. 4. 5 the second moment of area of the semicircular nose portion is

19. 1 Bending • Example 19. 1: (cont’d)
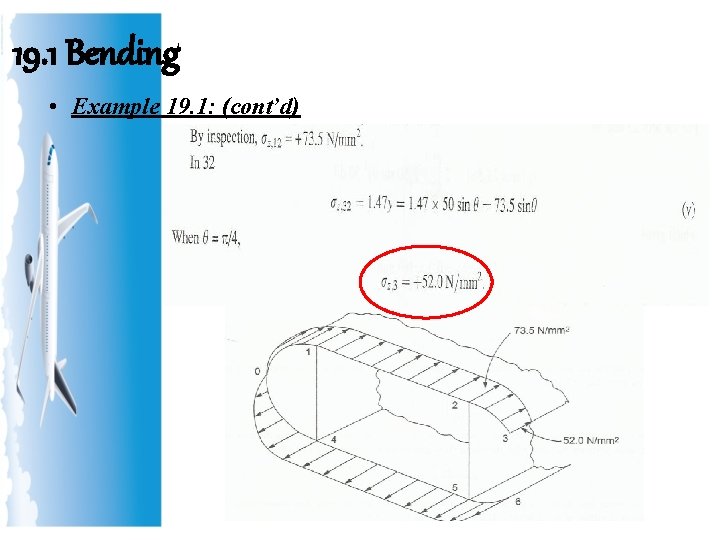
19. 1 Bending • Example 19. 1: (cont’d)

19. 2 Shear • Unlike the completely closed section case, shear loads must be applied through the shear center of the combined section; otherwise, shear stresses of the type described in section 18. 2 due to torsion arise. • Where shear loads do not act through the shear center, its position must be found and the loading system replaced by shear loads acting though the shear center together with a torque, the two loading cases are then analyzed separately. • Again, we assume that the cross section of the beam remains undistorted by the loading.
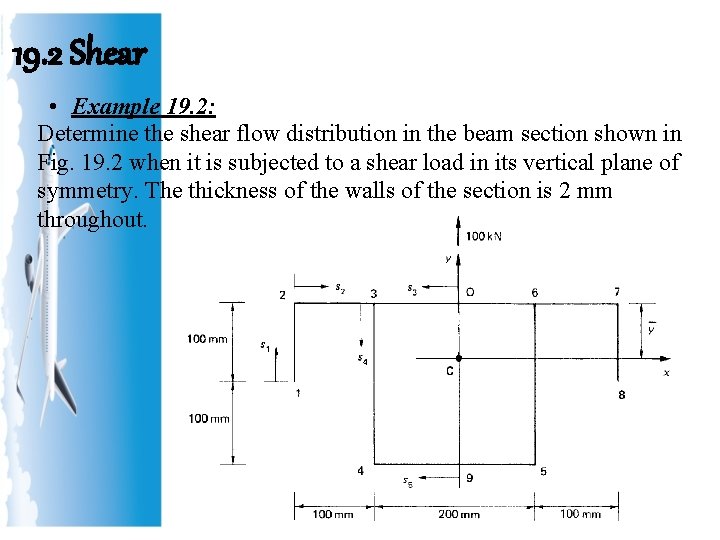
19. 2 Shear • Example 19. 2: Determine the shear flow distribution in the beam section shown in Fig. 19. 2 when it is subjected to a shear load in its vertical plane of symmetry. The thickness of the walls of the section is 2 mm throughout.

19. 2 Shear • Example 19. 2: (cont’d) The centroid of area C lies on the axis of symmetry at some distance. y from the upper surface of the beam section. Taking moments of area about this upper surface The second moment of area of the section about Cx is given by

19. 2 Shear • Example 19. 2: (cont’d) The section is symmetrical about Cy so that Ixy = 0, and since Sx = 0, the shear flow distribution in the closed section 3456 is, from Eq. (17. 15), Also, the shear load is applied through the shear center of the complete section—that is, along the axis of symmetry—so that in the open portions 123 and 678 the shear flow distribution is, from Eq. (17. 14),

19. 2 Shear • Example 19. 2: (cont’d) We note that the shear flow is zero at the points 1 and 8, and therefore the analysis may conveniently, though not necessarily, begin at either of these points. Thus, referring to Fig. 19. 4, Examination of Eq. (iii) shows that q 12 is initially positive and changes sign when s 1 = 50 mm. Further, q 12 has a turning value (dq 12/ds 1 = 0) at s 1 = 25 mm of 4. 3 N/mm. In the wall 23,

19. 2 Shear • Example 19. 2: (cont’d) To determine the shear flow distribution in the closed part of the section, we must use the method described in Section 16. 3, in which the line of action of the shear load is known. Thus, we “cut” the closed part of the section at some convenient point, obtain the qb or “open section” shear flows for the complete section, and then take moments as in Eqs. (17. 16) or (17. 17). However, in this case, we may use the symmetry of the section and loading to deduce that the final value of shear flow must be zero at the midpoints of the walls 36 and 45, that is, qs= qs, 0= 0 at these points. Hence,

19. 2 Shear • Example 19. 2: (cont’d) and q 3 =− 104 N/mm in the wall 03. It follows that for equilibrium of shear flows at 3, q 3, in the wall 34, must be equal to − 138. 5− 104= − 242. 5 N/mm. Hence, Examination of Eq. (vi) shows that q 34 has a maximum value of − 281. 7 N/mm at s 4 = 75 mm; also, q 4 =− 172. 5 N/mm. Finally, the distribution of shear flow in the wall 94 is given by
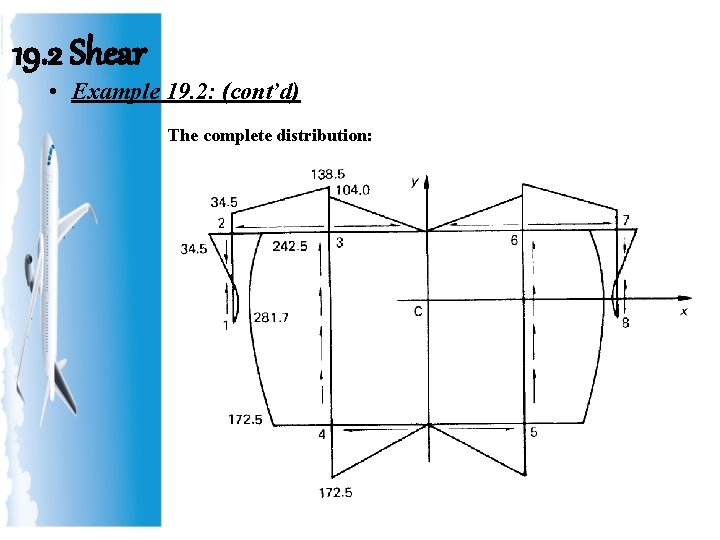
19. 2 Shear • Example 19. 2: (cont’d) The complete distribution:

19. 3 Torsion • Generally, in the torsion of composite sections, the closed portion is dominant, since its torsional stiffness is far greater than that of the attached open section portion which may therefore be frequently ignored in the calculation of torsional stiffness; shear stresses should, however, be checked in this part of the section.

19. 3 Torsion • Example 19. 3: Find the angle of twist per unit length in the wing whose cross section is shown in Fig. 18. 4 when it is subjected to a torque of 10 k. N m. Find also the maximum shear stress in the section. G=25000 N/mm 2. Wall 12 (outer)=900 mm. Nose cell area=20 000 mm 2.

19. 3 Torsion • Example 19. 3: (cont’d) It may be assumed, in a simplified approach, that the torsional rigidity GJ of the complete section is the sum of the torsional rigidities of the open and closed portions. For the closed portion, the torsional rigidity is, from Eq. (18. 4), The torsional rigidity of the open portion is found using Eq. (17. 11), thus

19. 3 Torsion • Example 19. 3: (cont’d) The torsional rigidity of the complete section is then In all unrestrained torsion problems, the torque is related to the rate of twist by the expression The angle of twist per unit length is therefore given by Substituting for T in Eq. (18. 1) from Eq. (18. 4), we obtain the shear flow in the closed section. Thus,

19. 3 Torsion • Example 19. 3: (cont’d) The maximum shear stress in the closed section is then 250/1. 5=166. 7 N/mm 2. In the open portion of the section, the maximum shear stress is obtained directly from Eq. (18. 10) and is

19. 3 Torsion • Example 19. 4: The wing section shown in Fig. 19. 7 is subjected to a vertical shear load of 50 k. N in the plane of the web 43. Determine the rate of twist of the section and the maximum shear stress. Take G=25000 N/mm 2.

19. 3 Torsion • Example 19. 4: (cont’d) The 50 k. N load acting in the plane of the web 43 must be replaced by a 50 k. N load acting through the shear center of the section together with a torque. Initially, therefore, we must find the position of the shear center which will, however, lie on the horizontal axis of symmetry. From section 16. 4. 5 To find the position of the shear center we apply an arbitrary shear load, Sy, through the shear center S as shown in Fig. 19. 7. Then, since Sx=0 and Ixy=0, Eq. (17. 15) reduces to

19. 3 Torsion • Example 19. 4: (cont’d) For the open part of the wing section qs, 0=0 at the open edges 1 and 6 while for the closed part of the section qs, 0 may be found using Eq. (17. 27) since the rate of twist will be zero for a shear load applied through the shear center. Then At the point 2, when s 1=25 mm, q 2=-1875(Sy/Ixx). In the wall 23 When s 2=100 mm, q 3= -11875(Sy/Ixx).

19. 3 Torsion • Example 19. 4: (cont’d) Now we “cut” the closed part of the section at 7. Then When θ=Π/2 at 3, qb, 3= -5000(Sy/Ixx). In the wall 34 From Eq. (17. 27)

19. 3 Torsion • Example 19. 4: (cont’d) Integrating and substituting the limits gives Now taking the moments about the center of the web 34 and substituting

19. 3 Torsion • Example 19. 4: (cont’d) The actual loading on the wing section of 50 k. N in the plane of the web is therefore equivalent to a 50 k. N load acting through the shear center together with an anticlockwise torque of 50 x 103 x 57. 7= 2885 Nm. The shear flow distribution due to the 50 k. N load acting through the shear center is given by Eqs. (ii), (iii), (vii), and (viii) in which Sy=50 k. N. Then The maximum shear flow in the wall 12 occurs, from Eq. (ix), at s 1=25 mm and is equal to -50. 1 N/mm.

19. 3 Torsion • Example 19. 4: (cont’d) • From Eq. (x) the maximum shear flow in the wall 23 occurs when s 2=100 mm and is equal to -320. 6 N/mm. • From Eq. (xi) the maximum shear flow in the wall 73 occurs when θ=0 and is equal to +169. 0 N/mm. • At 3 in the wall 73 the shear flow is 34. 0 N/mm. Also, in the wall 34 at 3, the shear flow, from Eq. (xii), is 286. 6 N/mm and the maximum value of the shear flow in the wall 34 occurs when s 3= 50 mm and is equal to -421. 6 N/mm.

19. 3 Torsion • Example 19. 4: (cont’d)

19. 3 Torsion • Example 19. 4: (cont’d) • We shall now examine the complete shear stress distribution to determine its maximum value. The maximum shear flow due to shear in the open part of the section occurs at 3 in the wall 23 and is 320. 6 N/mm so that the corresponding shear stress is 320. 6/2= 160. 3 N/mm 2 giving a maximum shear stress of 160. 3+9. 7 = 170. 0 N/mm 2. The maximum shear flow due to shear in the closed part of the section is 421. 6 N/mm in the direction 43 while the shear flow due to torsion is 363. 5 N/mm in the direction 34 giving a resultant shear flow of 421. 6 -363. 5 =58. 1 N/mm in the direction 43; the corresponding shear stress is 58. 1/4=14. 5 N/mm 2. At 3 in the web 34; the combined shear flow due to shear and torsion is 363. 5 286. 6=76. 9 N/mm in the direction 34; the corresponding shear stress is 76. 9/4= 19. 2 N/mm 2. In the wall 73 the maximum shear flow due to shear and torsion is 169. 0+363. 5 =532. 5 N/mm giving a shear stress of 532. 5/2=266. 3 N/mm 2. • We conclude, therefore, that the maximum shear stress in the combined section is 266. 3 N/mm 2 and occurs at point 7 in the wall 73.

! r e v O s i p i r T The t i d e y o j n e e v a h u o y e p Ho
- Slides: 30