Air Pollution Engineering EAT 301 AIR POLLUTION CONCENTRATION










































































- Slides: 105

Air Pollution Engineering (EAT 301) AIR POLLUTION CONCENTRATION MODEL

Air Pollution (AP) Concentration Models Fixed-box models Diffusion models Gaussian plume models Plume rise

Why do we need AP modeling ?

What is air pollution modeling ? Air pollution modeling are mathematical and numerical techniques to simulate the physical and chemical processes that affect air pollutant as they disperse and react in the atmosphere. Based on inputs of source information (e. g. emission rates, stack height) and meteorological data. They are used to: Compliance with DOE referring to EIA. (Health) risk analysis. Emergency planning.

Type of AP modeling Fixed-box models Single and multiple box models, with and without chemical reactions Dispersion (diffusion) models Single and multiple point sources Receptor models

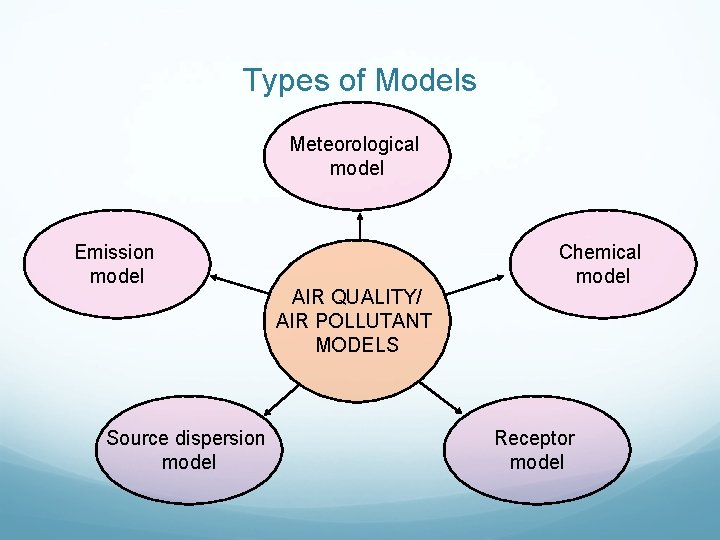
Types of Models Meteorological model Emission model Source dispersion model AIR QUALITY/ AIR POLLUTANT MODELS Chemical model Receptor model

Continue…. . Emission model Estimates temporal and spatial emission rates based on activity level, emission rate per unit of activity and meteorology. Meteorological model Describes transport, dispersion, vertical mixing and moisture in time and space. Chemical model Describes transformation of directly emitted particles and gases to secondary particles and gases; also estimates the equilibrium between gas and particles for volatile species. Source dispersion model Uses the outputs from the previous models to estimate concentrations measured at receptors; includes mathematical simulations of transport, dispersion, vertical mixing, deposition and chemical models to represent transformation. Receptor model Infers contributions from different primary source emissions or precursors from multivariate measurements taken at one ore more receptor sites.

Classification of AP models Developed for a number of pollutant types and time periods Short-term models – for a few hours to a few days; worst case episode conditions. Long-term models – to predict seasonal or annual average concentrations; health effects due to exposure. Classified by Non-reactive models – pollutants such as SO 2 and CO. Reactive models – pollutants such as O 3, NO 2, etc. Classified by coordinate system used Grid-based Region divided into an array of cells Trajectory Follow plume as it moves downwind Classified by level of sophistication Screening: simple estimation use preset, worst-case meteorological conditions to provide conservative estimates. Refined: more detailed treatment of physical and chemical atmospheric processes; require more detailed and precise input data.

USEPA AP models

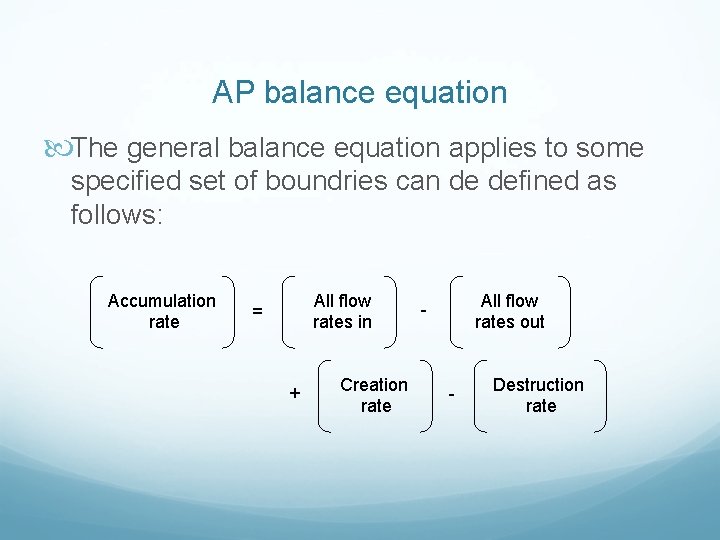
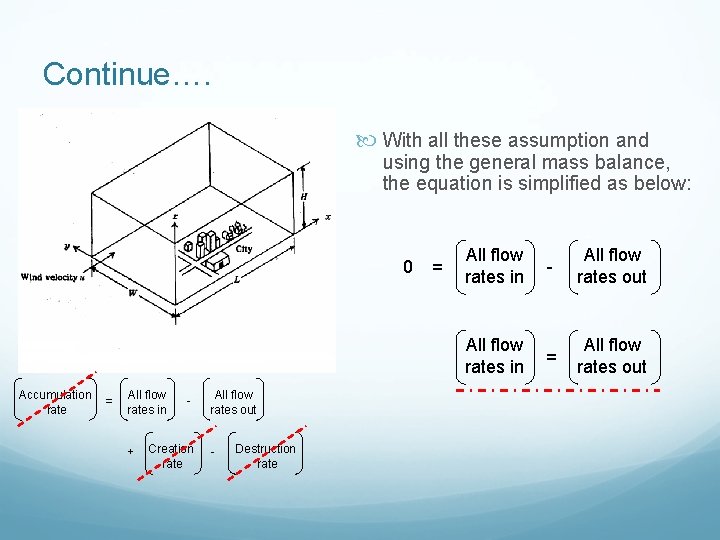
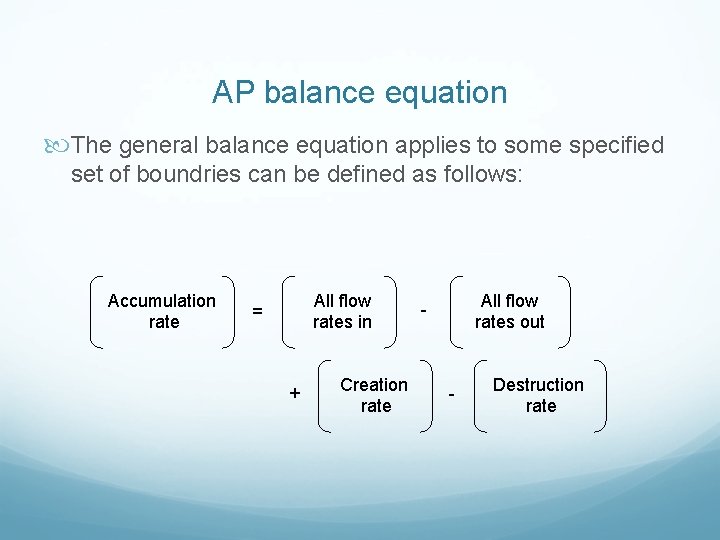
AP balance equation The general balance equation applies to some specified set of boundries can de defined as follows: Accumulation rate All flow rates in = + Creation rate All flow rates out - - Destruction rate

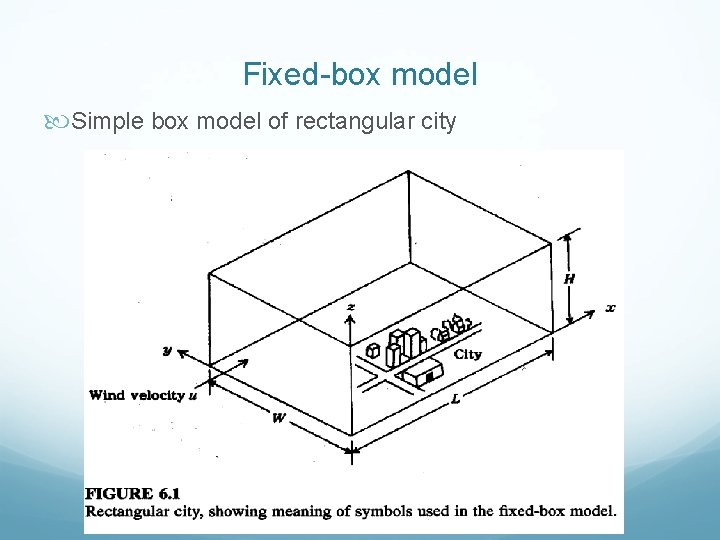
Fixed-box model Simple box model of rectangular city

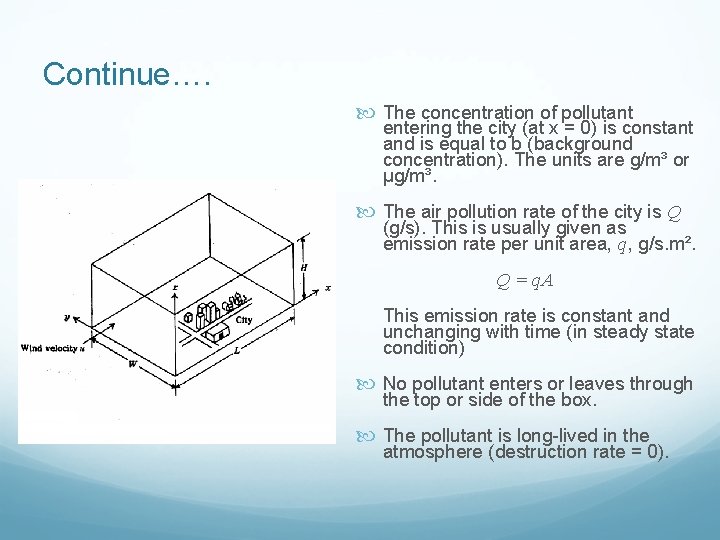
Fixed-box model Simple fixed-box model for a rectangular city: c – pollutant concentration in air living box b – pollutant concentration in entering air q – pollutant mass emission rate per unit area in the city (area source) L – length of box in direction of wind u – wind speed H – mixing height

Fixed-box model The city is a rectangle with dimension W and L and one side is parallel with wind direction. Complete atmospheric turbulence is produced and total mixing of pollutants up to H and no mixing above this height. The turbulence is strong enough in the upwind direction that the pollutant concentration is uniform in the whole volume of air over the city and not higher at downwind side than upwind side. The wind blows in x direction with velocity u. This velocity is constant and is independent of time, location or elevation above the ground (steady state condition). We use average u between at the ground (z=0) and at H.

Continue…. The concentration of pollutant entering the city (at x = 0) is constant and is equal to b (background concentration). The units are g/m³ or µg/m³. The air pollution rate of the city is Q (g/s). This is usually given as emission rate per unit area, q, g/s. m². Q = q. A This emission rate is constant and unchanging with time (in steady state condition) No pollutant enters or leaves through the top or side of the box. The pollutant is long-lived in the atmosphere (destruction rate = 0).

Continue…. With all these assumption and using the general mass balance, the equation is simplified as below: 0 = All flow rates in Accumulation rate = All flow rates in + - Creation rate All flow rates out - Destruction rate - All flow rates out = All flow rates out

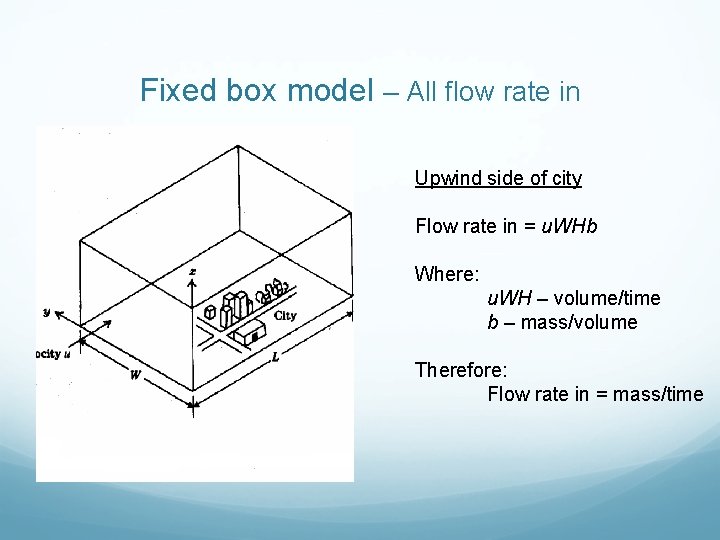
Fixed box model – All flow rate in Upwind side of city Flow rate in = u. WHb Where: u. WH – volume/time b – mass/volume Therefore: Flow rate in = mass/time

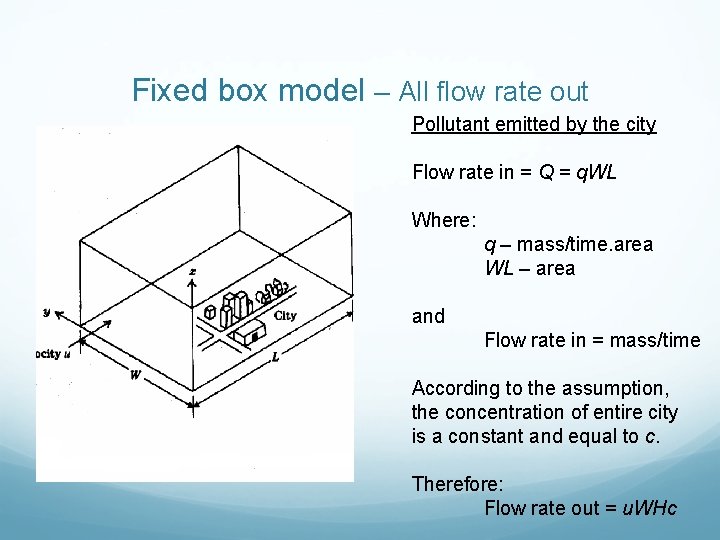
Fixed box model – All flow rate out Pollutant emitted by the city Flow rate in = Q = q. WL Where: q – mass/time. area WL – area and Flow rate in = mass/time According to the assumption, the concentration of entire city is a constant and equal to c. Therefore: Flow rate out = u. WHc

Continue…. Substitute these expression into E 1: E. 1

Fixed-box model – Example 1 A city with dimension W L H (7 km 13 km 1. 5 km) had a wind velocity of 4 m/s. The upwind concentration of SO 2 is 10 µg/m 3. The emission rate for the city is 4. 5 x 10 -6 g/s. m 2. What is the concentration of SO 2 over the city?

Example 1 - Answer W = 7 km L = 13 km H = 1. 5 km u = 4 m/s b = 10 µg/m 3 q = 4. 5 x 10 -6 g/s. m 2

Fixed-box model – Example 2 A city with dimension W L H (5 km 1 km) had a wind velocity of 3 m/s. The upwind concentration of CO 2 is 5 µg/m 3. The emission rate for the city is 4. 0 x 10 -6 g/s. m 2. What is the concentration of CO 2 over the city?

Example 2 - Answer W = 5 km L = 15 km H = 1 km u = 3 m/s b = 5 µg/m 3 q = 4. 0 x 10 -6 g/s. m 2

Fixed-box model The model indicates that the upwind concentration for a long lived pollutant is additive to the concentration produced by the city. From the pollutant concentration in the air living box (see equation), the concentration (c) increases with q and L and decreases with u and H. Most of the models predicts concentrations for only one specific meteorological condition. To calculate the annual average concentration of some pollutant, we need to calculate the concentration for each meteorological condition and then multiply by the frequency of occurrence for that meteorological condition.

Continue…. Annual average concentration = Over all meteorologies Concentration for that meteorology Frequency of occurrence of that meteorology

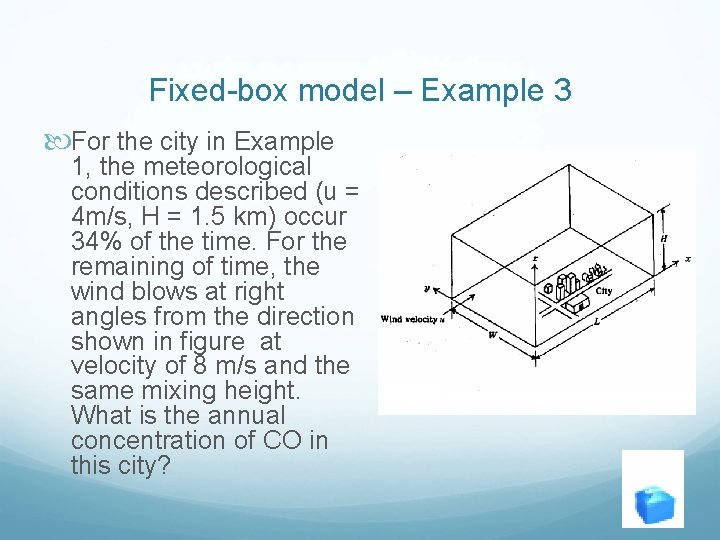
Fixed-box model – Example 3 For the city in Example 1, the meteorological conditions described (u = 4 m/s, H = 1. 5 km) occur 34% of the time. For the remaining of time, the wind blows at right angles from the direction shown in figure at velocity of 8 m/s and the same mixing height. What is the annual concentration of CO in this city?

Example 3 - Answer Find the concentration for another meteorology condition: W = 7 km L = 13 km H = 1. 5 km u = 8 m/s b = 10 µg/m 3 q = 4. 5 x 10 -6 g/s. m 2

Continue…. Therefore: Annual average concentration = Over all meteorologies Concentration for that meteorology Frequency of occurrence of that meteorology

Fixed-box model – Example 4 For the city in Example 1, the meteorological conditions described (u = 3 m/s, H = 1 km) occur 40% of the time. For the remaining 60%, the wind blows at right angle to the direction shown in figure at velocity of 6 m/s and the same mixing height. What is the annual concentration of CO in this city?

Example 4 - Answer Find the concentration for another meteorology condition: W = 5 km L = 15 km H = 1 km u = 6 m/s b = 5 µg/m 3 q = 4. 5 x 10 -6 g/s. m 2

Continue…. Therefore: Annual average concentration = Over all meteorologies Concentration for that meteorology Frequency of occurrence of that meteorology

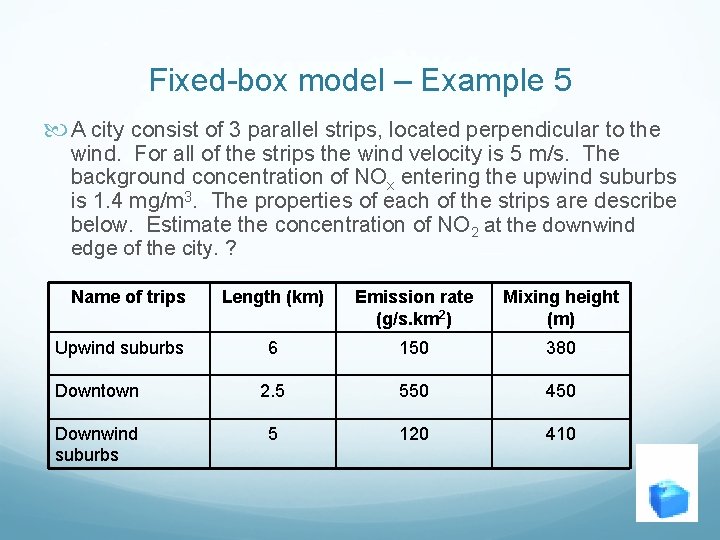
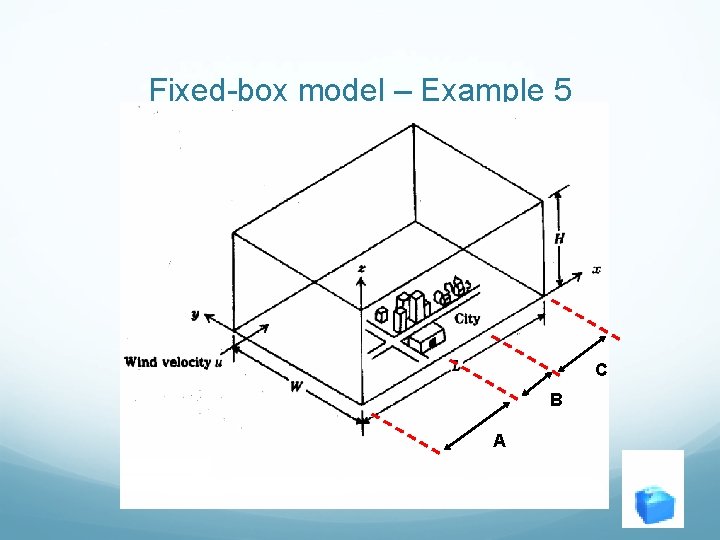
Fixed-box model – Example 5 A city consist of 3 parallel strips, located perpendicular to the wind. For all of the strips the wind velocity is 5 m/s. The background concentration of NOx entering the upwind suburbs is 1. 4 mg/m 3. The properties of each of the strips are describe below. Estimate the concentration of NO 2 at the downwind edge of the city. ? Name of trips Length (km) Emission rate (g/s. km 2) Mixing height (m) 6 150 380 Downtown 2. 5 550 450 Downwind suburbs 5 120 410 Upwind suburbs

Fixed-box model – Example 5 C B A

1 st Section L = 6 km H = 380 m u = 5 m/s b = 1. 4 mg/m 3 q = 150 g/s. km 2 Example 5 - Answer

2 nd Section L = 2. 5 km H = 450 m u = 5 m/s b = 1. 87 mg/m 3 q = 550 g/s. km 2 Example 5 - Answer

3 rd Section L = 5 km H = 410 m u = 5 m/s b = 2. 48 mg/m 3 q = 120 g/s. km 2 Example 5 - Answer


Diffusion models – Gaussian plume Objectives To develop dispersion model for point source using Gaussian plume model. Highlight the main parameters that influence the accuracy of the model. Explain briefly the algorithms used in the model

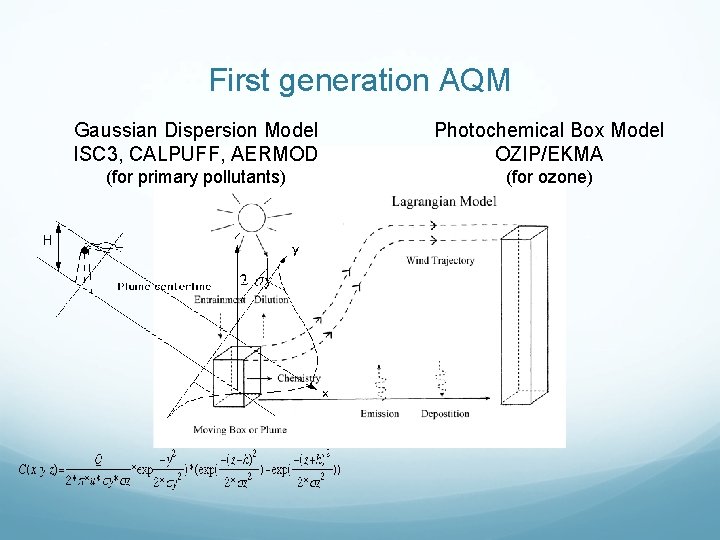
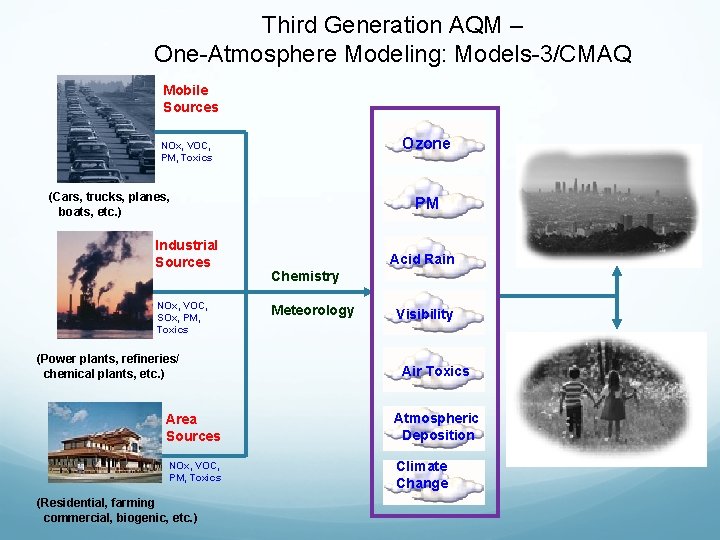
Evolution of air quality models (AQM) 1 st generation AQM (1970 s - 1980 s) Dispersion Models (e. g. , Gaussian Plume Models-ISC) Photochemical Box Models (e. g. OZIP/EKMA) 2 nd generation AQM (1980 s - 1990 s) Photochemical Grid Models (e. g. , UAM, RADM) 3 rd generation AQM (1990 s - 2000 s) Community-Based ‘One-Atmosphere’ Modeling System (e. g. , U. S. EPA’s Models-3/CMAQ)

First generation AQM Gaussian Dispersion Model ISC 3, CALPUFF, AERMOD Photochemical Box Model OZIP/EKMA (for primary pollutants) (for ozone)

Second generation AQM Eulerian Grid Models UAM, RADM, REMSAD, ROM

Third Generation AQM – One-Atmosphere Modeling: Models-3/CMAQ Mobile Sources Ozone NOx, VOC, PM, Toxics (Cars, trucks, planes, boats, etc. ) Industrial Sources NOx, VOC, SOx, PM, Toxics (Power plants, refineries/ chemical plants, etc. ) Area Sources NOx, VOC, PM, Toxics (Residential, farming commercial, biogenic, etc. ) PM Acid Rain Chemistry Meteorology Visibility Air Toxics Atmospheric Deposition Climate Change

Diffusion models – Gaussian plume It is a material balance model. Most widely used techniques for estimating the impact of non-reactive pollutants. Source of air pollutants Point sources (e. g. stack) Line sources (e. g. roads) Area sources (e. g. treatment ponds) Volume sources (e. g. buildings) Most of the emission releases into the atmosphere are point sources.

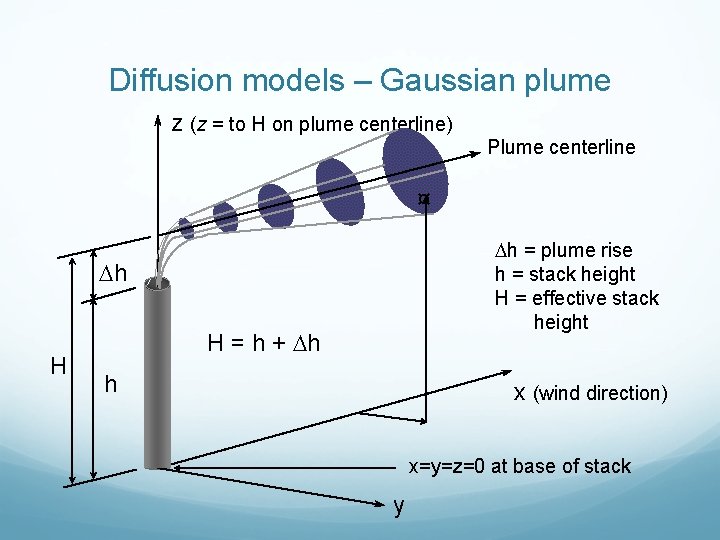
Diffusion models – Gaussian plume z (z = to H on plume centerline) Plume centerline ¤ h = plume rise h = stack height H = effective stack height h H H = h + h h x (wind direction) x=y=z=0 at base of stack y

Gaussian plume Assumptions: The plume is assumed to be emitted from a point with coordinated 0, 0, H. The smoke emitted at the point source is assumed to be a nonbuoyant pollutant at emission rate Q (g/s) and blows in x direction with velocity u that independent of time, elevation or location. The problem is to compute the concentration due to this source at any point (x, y, z) for x>0. This approach tries to calculate the average value without making any statement about instantaneous values.

Plume shapes and typical velocity

AP balance equation The general balance equation applies to some specified set of boundries can be defined as follows: Accumulation rate All flow rates in = + Creation rate All flow rates out - - Destruction rate

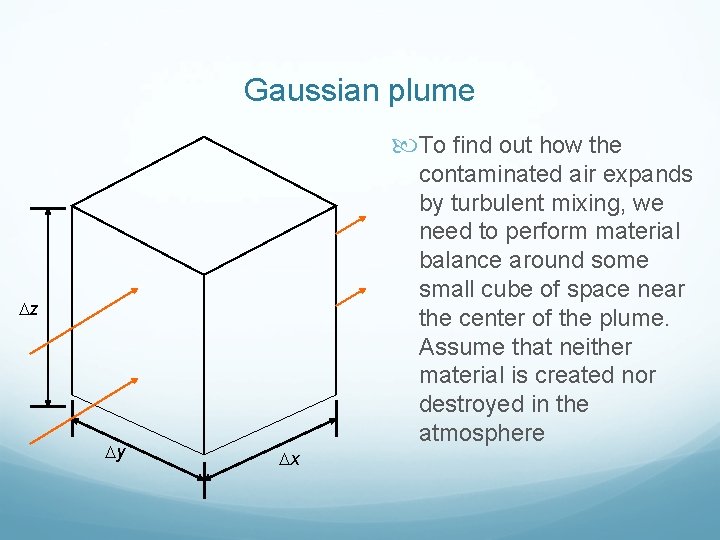
Gaussian plume To find out how the contaminated air expands by turbulent mixing, we need to perform material balance around some small cube of space near the center of the plume. Assume that neither material is created nor destroyed in the atmosphere z y x

Gaussian plume Accumulation rate All flow rates in = + Creation rate All flow rates out - - Destruction rate Therefore: Accumulation rate = (all flow rates in) – (all flow rates out)

Gaussian plume The accumulation rate is the time derivative of the amount contained that is concentration and volume. But the volume of the cube is not changing with time. There will be no bulk flow (e. g. convection) into or out of the cube because the cube is moving with the local wind velocity. However, there are flows through all the surfaces of the cube due to turbulent mixing.

Continue…. The flux of material being mixed across any surface is given by where: c – concentration n – distance in the direction (normally x, y or z) K – turbulent dispersion coefficient

Continue…. Flux, must have units of mass/time. area (g/s. m 2). c/ n, has a dimension of mass/length 4. K (eddy diffusitivity), must have dimensions of length 2/time (e. g. m 2/s). –ve, indicate that the flow is from higher concentration to low. Gradient transport or K theory or first order closure approach.

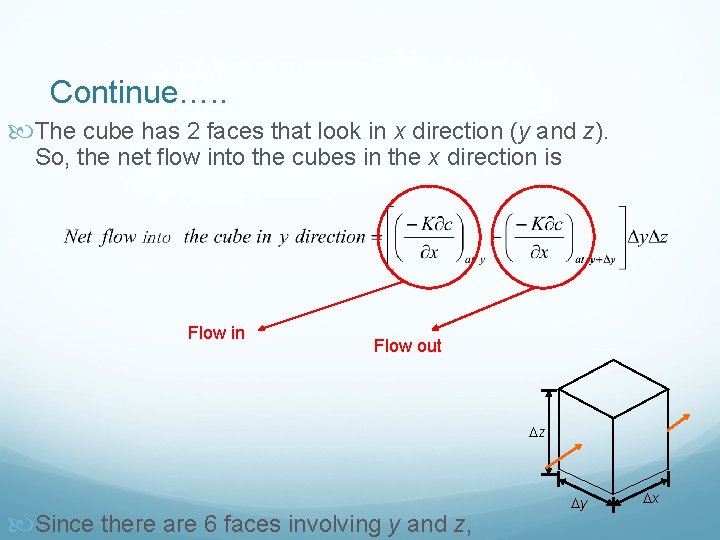
Continue…. . The cube has 2 faces that look in x direction (y and z). So, the net flow into the cubes in the x direction is Flow in Flow out z Since there are 6 faces involving y and z, y x

Continue…. E. 1 E. 2 Accumulation rate = (all flow rates in) – (all flow rates out) E. 3 Therefore: Substitute E. 1 and E. 2 into E. 3 and divided both sides with x y z…….

Continue….

Continue…. But…… So that if we take the limit of an infinitesimally small cube, it becomes…. Since experimental data indicates that for turbulent diffusion in the atmosphere the values of K in the 3 directions are not the same, therefore

Continue…. . The Gaussian plume equation is regularly applied to pollutant spreading in 1, 2 or 3 dimensions. By using equation below, the 1, 2 or 3 dimensions are as follows:

Continue…. . One dimension: Two dimension: Three dimension:

Gaussian plume – 2 -D spreading To use the 2 dimensions equation for problems solving, the material balances and substitutions had been made as follows: Where: c - mean concentration of diffusing substance (kg/m 3) y and z are called horizontal and vertical dispersion coefficients (m) Q - contaminant emission rate (g/s); lateral dispersion coefficient function (m); vertical dispersion coefficient function (m)

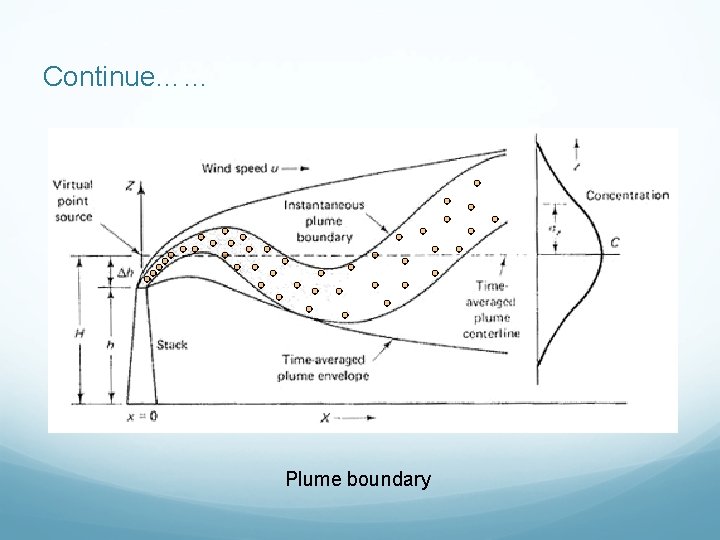
Continue…… Plume boundary

Continue…. If we set y = (z - H) = 0, then exp 0 = 1. This shows the concentration on the centerline of the plume. The two values show that this centerline concentration decrease with the downwind distance. Hence, the concentration decreases as the plume move in the

Example 1 A factory emits 34 g/s of SO 2 at height H. The wind speed is 5 m/s. At a distance of 1 km downwind, the values of y and z are 24 m and 37 m, respectively. What are the concentration of SO 2 at the centerline of the plume, and at a point 60 m to the side and 20 m below the centerline?

Answer 1 Q = 34 g/s u = 5 m/s y = 24 m z= 37 m

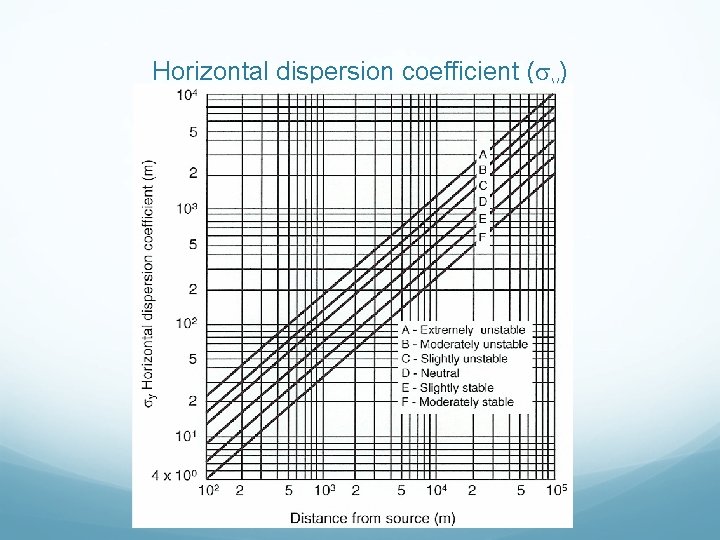
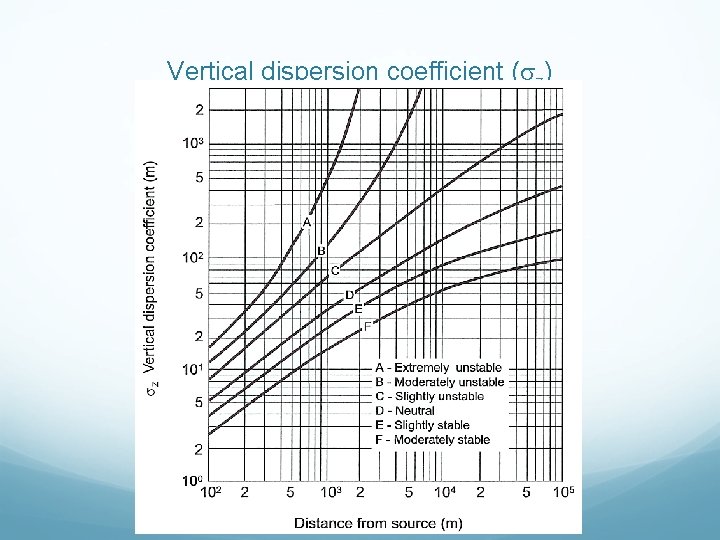
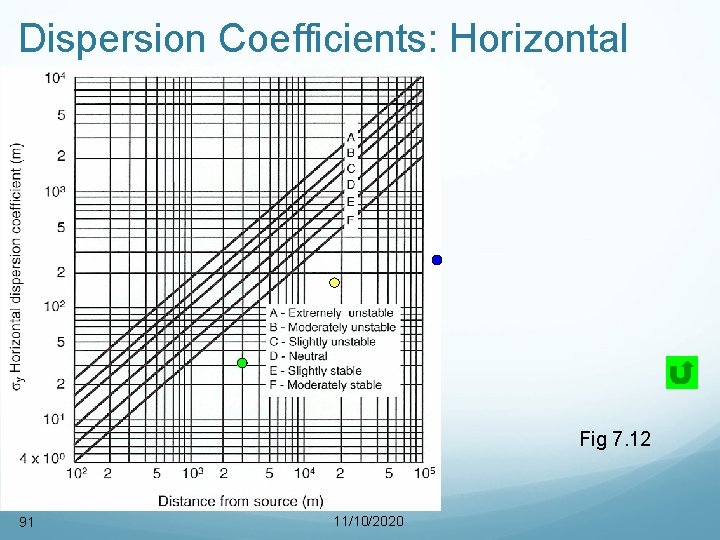
Gaussian plume – 2 -D spreading The basic Gaussian plume equation predicts a plume that is symmetrical with respect to y and z and ignoring the ground level effect (H). Different values of y and z mean that the spreading in the vertical and horizontal directions is not equal. Usually y > z. The horizontal dispersion coefficient ( y) forms a family of a straight lines (for various atmospheric conditions) with slope of 0. 894.

Horizontal dispersion coefficient ( y)

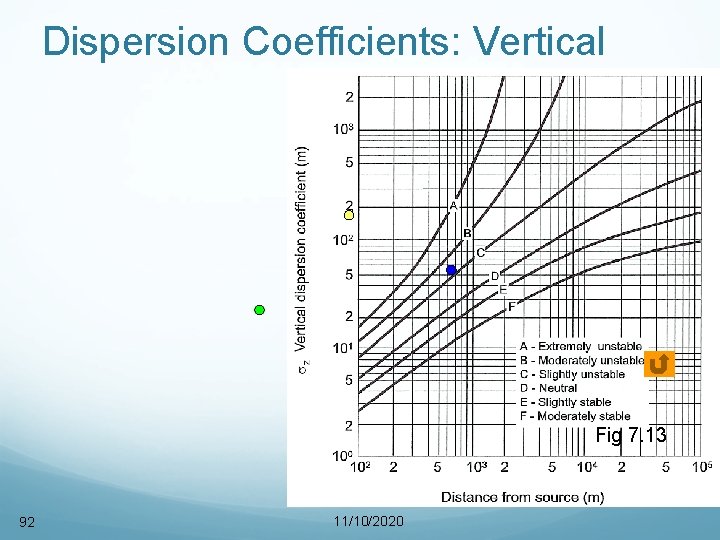
Vertical dispersion coefficient ( z)

Continue…. Clear and hot weather with low wind speed The air near the ground is heated by the sun causing the air to rise and thus cause the pollutant to mix. The atmosphere is unstable thus the values of y and z will be larger. Cloudless cold night The ground is cooled by radiation and thus cooled the air near the ground. The air are in inversion layer, making the atmosphere stable and inhibit the pollutant the values of y and z will be small.

Continue…. The horizontal ( y) and vertical ( z) dispersion coefficient along with Gaussian plume 2 -D equation are able to predict downwind concentrations from the point source. This is the most widely used method for routine calculations of air pollutant dispersion from the point source. These plots are based on measurements for x 1. The values beyond that are based on extrapolations.

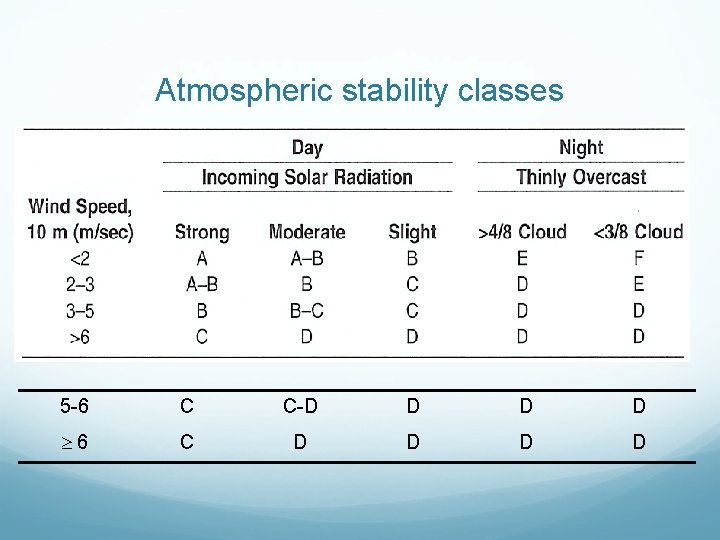
Atmospheric stability classes 5 -6 C C-D D 6 C D D

Example 2 Estimate the values of y and z at a point of 0. 7 km downwind from a pollutant source on a bright sunny day with the wind speed 6 m/s. Answer 2 Stability category – C y – 70 m z – approx. 45 m

Example 3 An industrial boiler is burning at 12 tons of 2. 5% sulfur coal/hr with an emission rate of 151 g/s. The operation was conducted during night time with thick clouds. The following exist : H = 120 m, u = 2 m/s. Determine the. …. i. Stability class ? ii. y ? iii. z ? iv. Concentration of SO 2 at the centerline of the plume and at a point 1 km to the side and 10 m below the centerline ?

Answer 3 i. Stability class D. ii. y is approx. 70 m. iii. z is 35 m. iv. C = 2. 37 10 -41 g/m 3

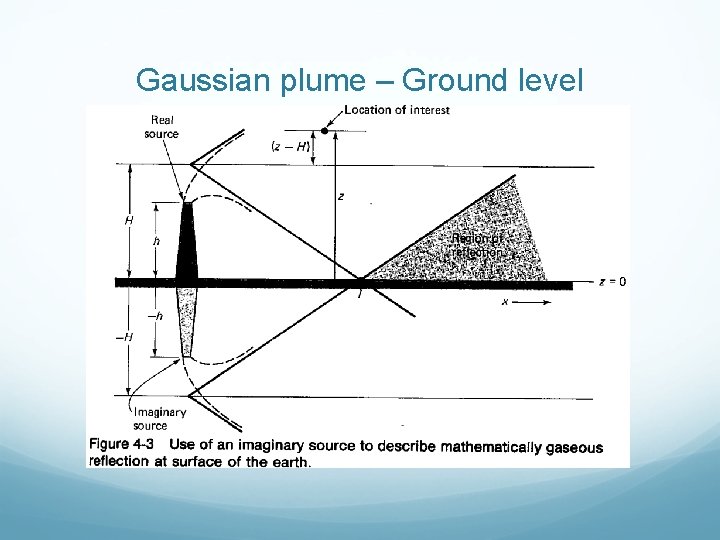
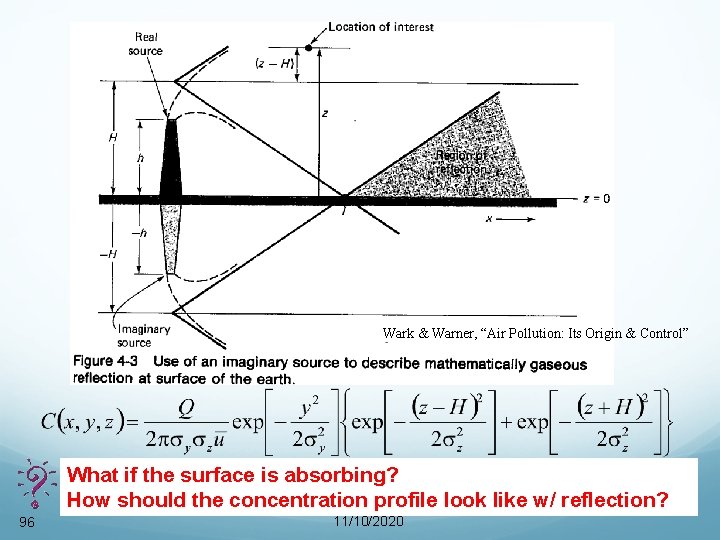
Gaussian plume – Ground level The up and downwards random atmospheric motion that spread the plume in vertical direction cannot penetrate the ground. Hence, the vertical spreading terminate at z=0. It is assumed that the pollutant is reflected upward as if the ground is a mirror. To compute the concentration that consider the ground effect, the equation is similar to the previous one accept for additional of mirror image plume, (z+H)2.

Gaussian plume – Ground level

Gaussian plume – Ground level If z=H, the main plume has a high concentration (in the air). Whereas the mirror-image plume has a small number [exp -½ (2 H/ z)2].

Example 4 A factory emits 20 g/s of CO at height (H) of 20 m. The wind speed is 5 m/s at distance 0. 5 km downwind for C stability. What are the CO concentration at a point of 25 m to the side and 2 m above the ground ? H = 20 m Q = 20 g/s u = 5 m/s Stability C y = 50 m z= 30 m

Answer 4

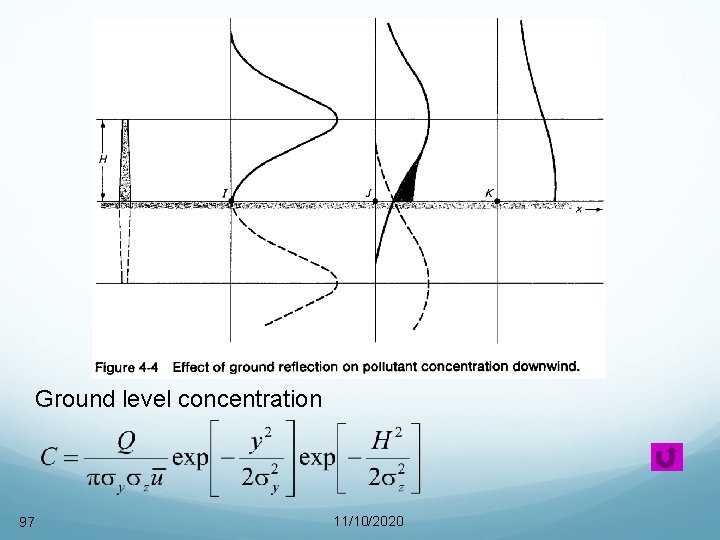
Gaussian plume – Ground level When z=0, the main plume and the mirror-image plume have the same value (at the ground level). When y=0 and z=0, which correspond to the line on the ground directly under the center of the plume

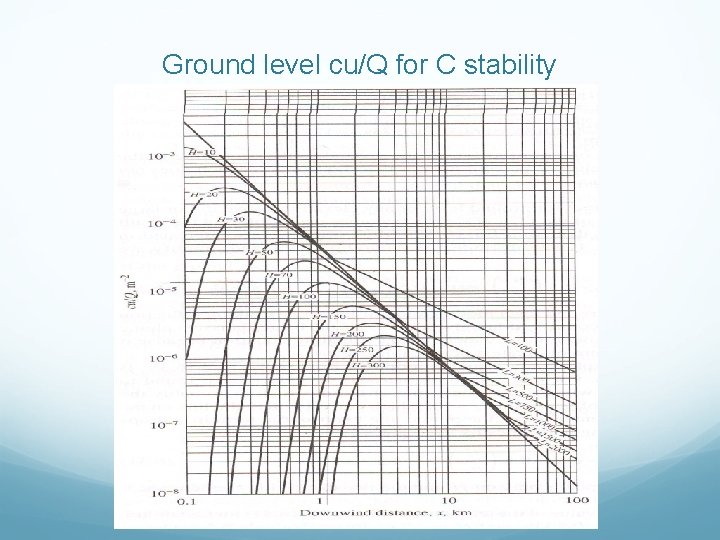
Ground level cu/Q for C stability

Example 5 A large copper smelter has a stack of 150 m high and a plume rise of 75 m. It is currently emitting 1000 g/s of SO 2. Estimate the ground level concentration of SO 2 from this point source at a distance of 5 km directly downwind when the wind speed is 3 m/s and the stability class is C? h = 150 m Q = 1000 g/s u = 5 m/s Stability C y = 400 m z= 250 m

Answer 5

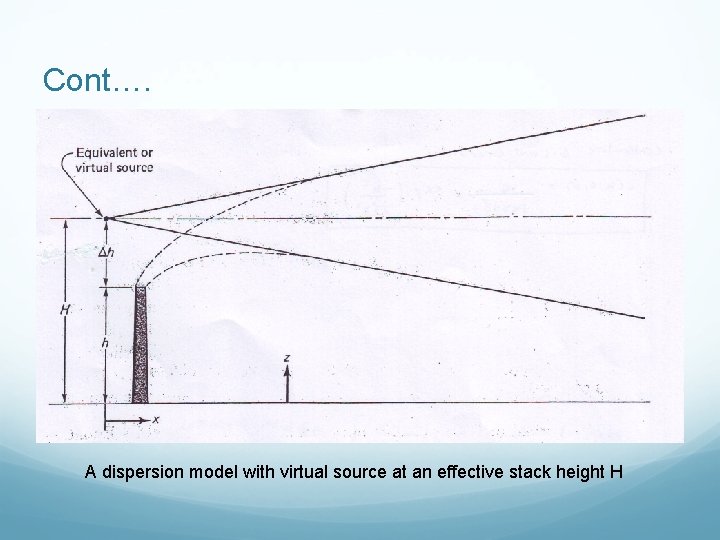
Plume rise Thermal power plants, petrochemical industries and factories (e. g. oil palm mill) releases emissions into the atmosphere. These emissions will rise from the stack the a plume will occurred which moves horizontally. Plume rise buoyantly because: They are hotter than the surrounding air. They exit the stack with vertical velocity. They stop rising because as they mix with the surrounding air, they lose the velocity and cool by mixing. Finally, the plume will settled in the atmosphere when the temperature is the same with atmosphere.

Cont…. A dispersion model with virtual source at an effective stack height H

Cont…. . 83 To calculate the plume rise: h - plume rise (m) Vs = stack exit velocity (m/s) D = stack diameter (m)

Example 6 Estimate the plume rise for a 2 m diameter stack whose the exit gas has a velocity of 34 m/s when the wind velocity is 4 m/s, the pressure is 1 atm and the stack and surrounding temperatures are 85 OC and 33 OC respectively. Vs = 34 m/s D=2 m u = 4 m/s P = 1 atm (1013 milibar) Ts = 85 o. C (358 K) Ta = 33 o. C (306 K)

Answer 6



Gaussian Dispersion Models Most widely used Based on the assumption plume spread results primarily by molecular diffusion horizontal and vertical pollutant concentrations in the plume are normally distributed (double Gaussian distribution) X Plume spread and shape vary in response to Z meteorological conditions Q u Y H 88 11/10/2020

Model Assumptions Gaussian dispersion modeling based on a number of assumptions including Steady-state conditions (constant source emission strength) Wind speed, direction and diffusion characteristics of the plume are constant Mass transfer due to bulk motion in the x-direction far outshadows the contribution due to mass diffusion Conservation of mass, i. e. no chemical transformations take place Wind speeds are >1 m/sec. Limited to predicting concentrations > 50 m downwind 89 11/10/2020

Gaussian Dispersion Equation Why isn’t x in the equation? Atmospheric Stability Classes Table 7. 4 90 11/10/2020

Dispersion Coefficients: Horizontal Fig 7. 12 91 11/10/2020

Dispersion Coefficients: Vertical Fig 7. 13 92 11/10/2020

Gaussian Dispersion Equation If the emission source is at ground level with no effective plume rise then Plume Rise • H is the sum of the physical stack height and plume rise. 93 11/10/2020

Plume Rise Buoyant plume: Initial buoyancy >> initial momentum Forced plume: Initial buoyancy ~ initial momentum Jet: Initial buoyancy << initial momentum For neutral and unstable atmospheric conditions, buoyant rise can be calculated by where buoyancy flux is 94 Vs: Stack exit velocity, m/s d: top inside stack diameter, m Ts: stack gas temperature, K Ta: ambient temperature, K g: gravity, 9. 8 m/s 2 11/10/2020

Carson and Moses: vertical momentum & thermal buoyancy, based on 615 observations involving 26 stacks. (heat emission rate, k. J/s) (stack gas mass flow rate. kg/s) When pollutants are dispersed to the ground level, how should we handle the situation? 95 11/10/2020

Wark & Warner, “Air Pollution: Its Origin & Control” What if the surface is absorbing? How should the concentration profile look like w/ reflection? 96 11/10/2020

Ground level concentration 97 11/10/2020

Maximum Ground Level Concentration Under moderately stable to near neutral conditions, The ground level concentration at the center line is The maximum occurs at Once z is determined, x can be known and subsequently C. 98 11/10/2020

Example An industrial boiler is burning at 12 tons (10. 9 mton) of 2. 5% sulfur coal/hr with an emission rate of 151 g/s. The following exist : H = 120 m, u = 2 m/s, y = 0. It is one hour before sunrise, and the sky is clear. Determine downwind ground level concentration at 10 km. Stability class = y = z = C(10 km, 0, 0) = 99 11/10/2020

Exercise If emissions are from a ground level source with H = 0, u = 4 m/s, Q = 100 g/s, and the stability class = B, what is downwind concentration at 200 m? At 200 m: y = z = C(200 m, 0, 0) = 100 11/10/2020

Example Calculate H using plume rise equations for an 80 m high source (h) with a stack diameter = 4 m, stack velocity = 14 m/s, stack gas temperature = 90 o C (363 K), ambient temperature = 25 o. C (298 K), u at 10 m = 4 m/s, and stability class = B. Then determine MGLC at its location. F= h plume rise = H= z = 101 Residents y = around Florida Rock Cement Plant are complaining its emission being violating its allowed level. The plant has its facility within 0. 5 km diameter. Its effective stack height is 60 m. You are a FLDEP environmental Cmax = Where are you going to locate your air quality monitors? Why? specialist. 11/10/2020

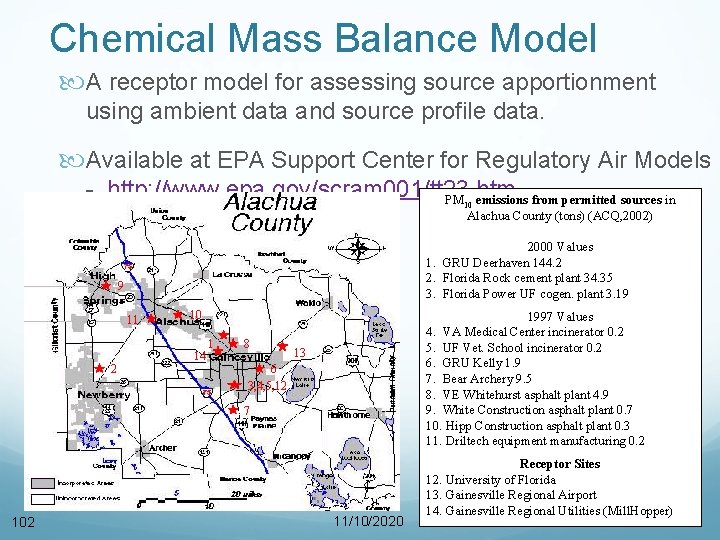
Chemical Mass Balance Model A receptor model for assessing source apportionment using ambient data and source profile data. Available at EPA Support Center for Regulatory Air Models - http: //www. epa. gov/scram 001/tt 23. htm PM emissions from permitted sources in 10 Alachua County (tons) (ACQ, 2002) 2000 Values 1. GRU Deerhaven 144. 2 2. Florida Rock cement plant 34. 35 3. Florida Power UF cogen. plant 3. 19 9 11 10 14 2 1 8 1997 Values 4. VA Medical Center incinerator 0. 2 5. UF Vet. School incinerator 0. 2 6. GRU Kelly 1. 9 7. Bear Archery 9. 5 8. VE Whitehurst asphalt plant 4. 9 9. White Construction asphalt plant 0. 7 10. Hipp Construction asphalt plant 0. 3 11. Driltech equipment manufacturing 0. 2 13 6 3, 4, 5, 12 7 102 11/10/2020 Receptor Sites 12. University of Florida 13. Gainesville Regional Airport 14. Gainesville Regional Utilities (Mill. Hopper)

Principles • Mass at a receptor site is a linear combination of the mass contributed from each of a number of individual sources; • Mass and chemical compositions of source emissions are conserved from the time of emission to the time the sample is taken. Cij = Σ(aik×Skj) Cij is the concentration of species ith in the sample jth measured at the receptor site: aik is the mass fraction of the species in the emission from source kth, and Skj is the total mass contribution from source kth in the jth sample at the receptor site. 103 11/10/2020

Example Total Pb concentration (ng/m 3) measured at the site: a linear sum of contributions from independent source types such as motor vehicles, incinerators, smelters, etc Pb. T = Pbauto + Pb incin. + Pbsmelter +… Next consider further the concentration of airborne lead contributed by a specific source. For example, from automobiles in ng/m 3, Pbauto, is the product of two cofactors: the mass fraction (ng/mg) of lead in automotive particulate emissions, a. Pb, auto, and the total mass concentration (mg/m 3) of automotive emission to the atmosphere, Sauto Pbauto = aauto (ng/mg) × Sauto (mg/m 3 air) 104 11/10/2020

Assumptions Composition of source emissions is constant over period of time, Chemicals do not react with each other, All sources have been identified and have had their emission characterized, including linearly independent of each other, The number of source category (j) is less than or equal to the number of chemical species (i) for a unique solution to these equations, and The measurement uncertainties are random, uncorrelated, and normally distributed (EPA, 1990). 105 11/10/2020