Aim To understand Stewarts Theorem DO NOW TAKE

Aim: To understand Stewart’s Theorem DO NOW: TAKE OUT CALCULATOR DEFINE CEVIAN A cevian is a straight line that passes through a vertex of a triangle or tetrahedron and intersects the opposite side or face.

Stewart’s Theorem �Matthew Stewart (1717– 1785) published this theorem as Proposition II on page 2 in his 1746 book. �It is said that Archimedes used theorem though (300 B. C. ) �In geometry, Stewart's theorem yields a relation between a lengths of the sides of the triangle and the length of a cevian of the triangle.

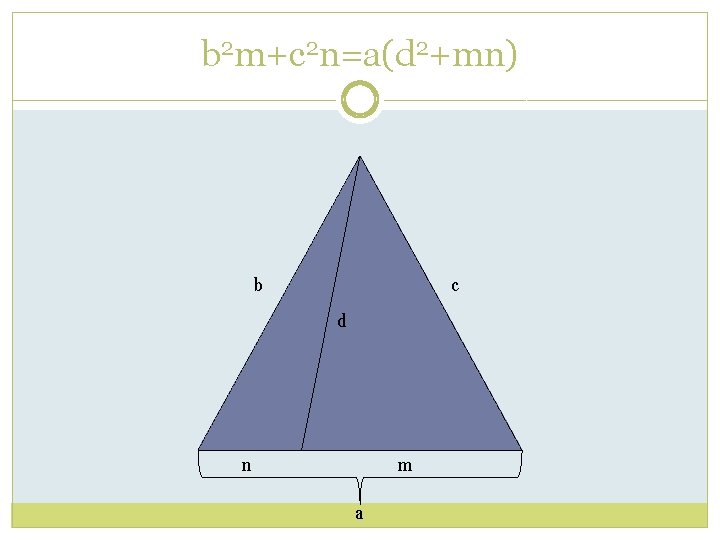
b 2 m+c 2 n=a(d 2+mn) b c d n m a

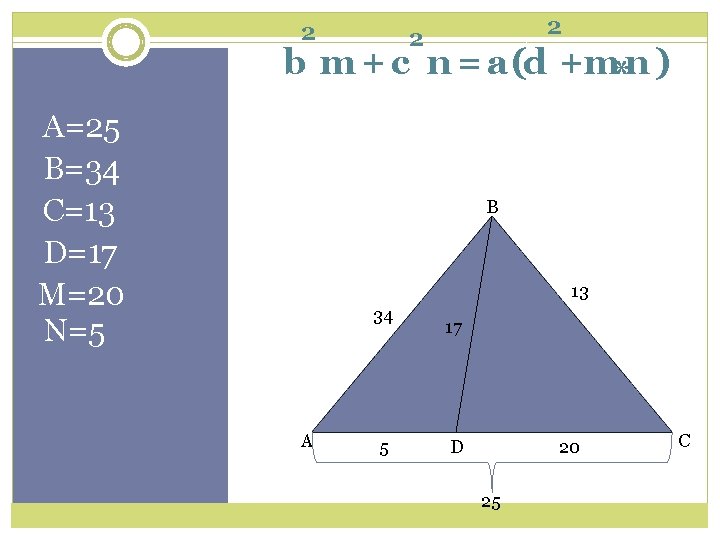
2 2 2 b m + c n = a(d +m*n ) A=25 B=34 C=13 D=17 M=20 N=5 B 13 34 A 5 17 D 20 25 C

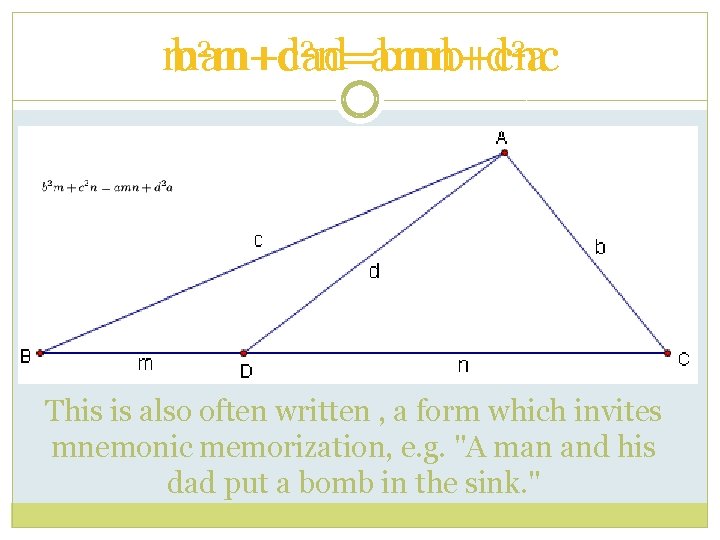
man+dad=bmb+cnc b 2 m+c 2 n=amn+d 2 a This is also often written , a form which invites mnemonic memorization, e. g. "A man and his dad put a bomb in the sink. "

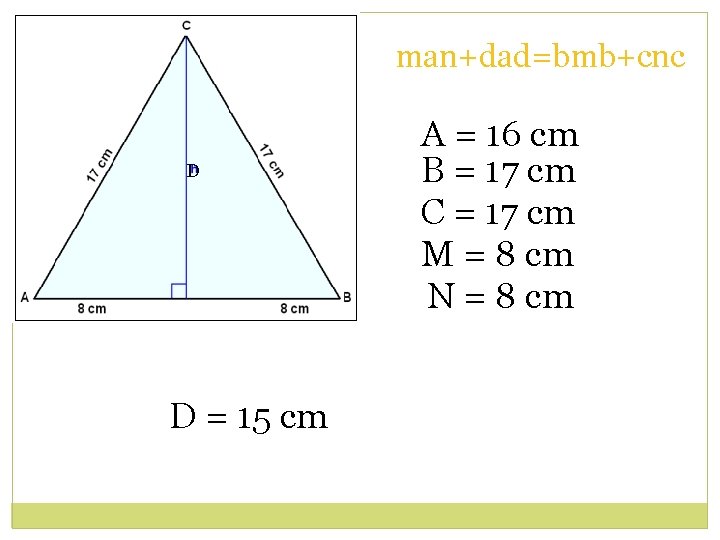
man+dad=bmb+cnc D D = 15 cm A = 16 cm B = 17 cm C = 17 cm M = 8 cm N = 8 cm

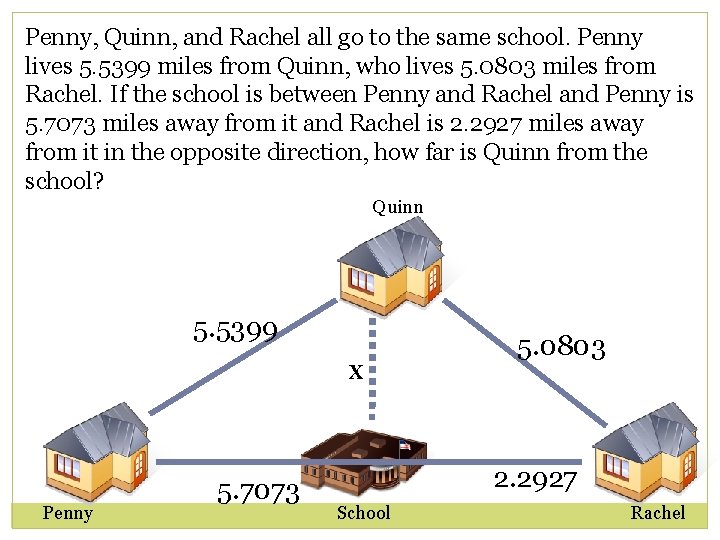
Penny, Quinn, and Rachel all go to the same school. Penny lives 5. 5399 miles from Quinn, who lives 5. 0803 miles from Rachel. If the school is between Penny and Rachel and Penny is 5. 7073 miles away from it and Rachel is 2. 2927 miles away from it in the opposite direction, how far is Quinn from the school? Quinn 5. 5399 x Penny 5. 7073 5. 0803 2. 2927 School Rachel

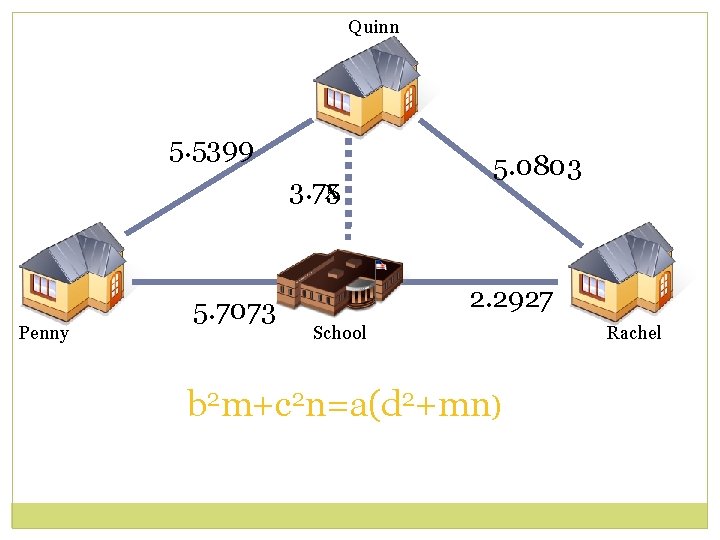
Quinn 5. 5399 3. 75 x Penny 5. 7073 5. 0803 2. 2927 School b 2 m+c 2 n=a(d 2+mn) Rachel

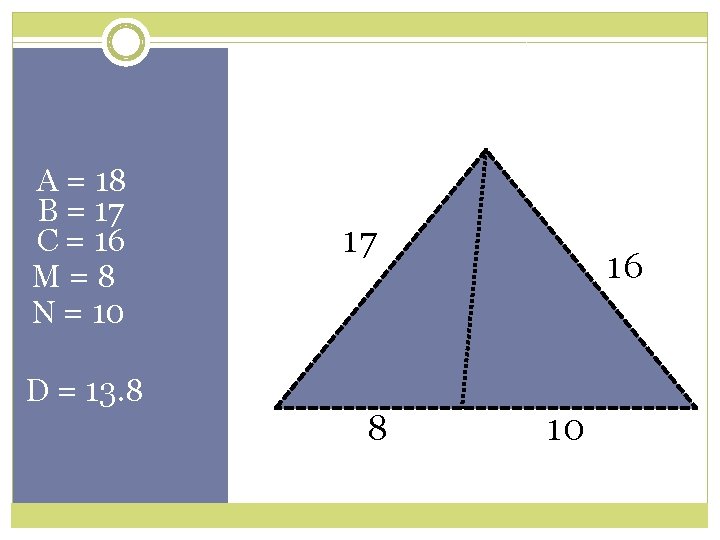
A = 18 B = 17 C = 16 M=8 N = 10 D = 13. 8 17 8 16 10

If the cevian happens to be a median, angle bisector, or altitude the following formulas can be used MEDIAN ANGLE BISECTOR ALTITUDE

Sources 1. HTTP: //EASYCALCULATION. COM/THEORE 2. 3. 4. 5. MS/STEWART-OR-APOLLONIUS. PHP HTTP: //MATH. STACKEXCHANGE. COM/QUE STIONS/46616/PROVING-STEWARTSTHEOREM-WITHOUT-TRIG HTTP: //WWW. ANSWERS. COM/TOPIC/CEVI AN-MATHEMATICS HTTP: //WWW. ARTOFPROBLEMSOLVING. C OM/WIKI/INDEX. PHP/STEWART'S_THEOR EM HTTP: //WWW. MS. UKY. EDU/~DROYSTER/C OURSES/FALL 11/MA 341/CLASSNOTES/LEC TURE%2013%20 HANDOUTS. PDF