Aim How do we make polynomial approximations for

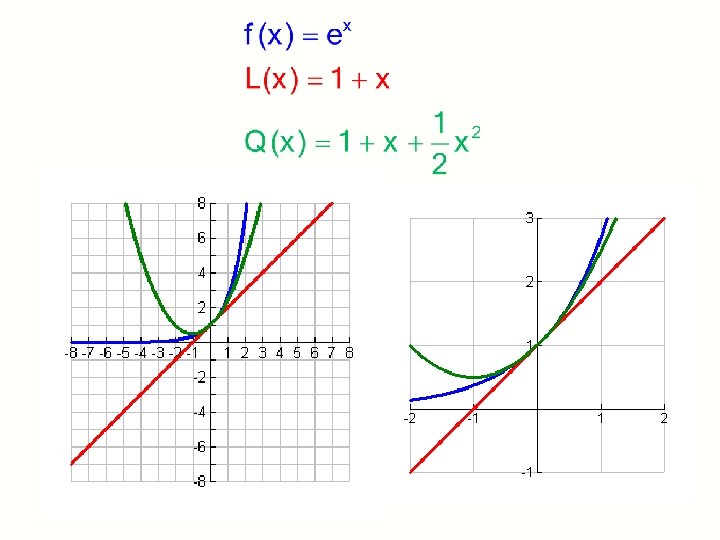
Aim: How do we make polynomial approximations for a given function ? Do Now: Find both the local linear and the local quadratic approximations of x f(x) = e at x = 0

we want to find a second degree polynomial of the form: that approximates the behavior of at If we make , and the first, and the second, derivatives the same, then we would have a pretty good approximation.

Suppose we wanted to find a fourth degree polynomial of the form: that approximates the behavior of at If we make , and the first, second, third and fourth derivatives the same, then we would have a pretty good approximation.

If we plot both functions, we see that near zero the functions match very well!

Our polynomial: has the form: or: This pattern occurs no matter what the original function was!

Maclaurin Series: (generated by f at ) If we want to center the series (and it’s graph) at some point other than zero, we get the Taylor Series: (generated by f at )

Taylor Series Brook Taylor was an accomplished musician and painter. He did research in a variety of areas, but is most famous for his development of ideas regarding infinite series. Brook Taylor 1685 - 1731 Greg Kelly, Hanford High School, Richland, Washington

What are the Taylor Series for some common functions ? Write the Taylor Series for f(x) = cos x centered at x = 0.

The more terms we add, the better our approximation.

For use the Ratio Test to determine the interval of convergence.

If the limit of the ratio between consecutive terms is less than one, then the series will converg The interval of convergence is

When referring to Taylor polynomials, we can talk about number of terms, order or degree. This is a polynomial with 3 positive terms. It is a 4 th order Taylor polynomial, because it was found using the 4 th derivative. It is also a 4 th degree polynomial, because x is raised to the 4 th power. The 3 rd order polynomial for degree 2. is , but it is x 3 term dropsrequired out when using the third derivative. AThe recent AP exam the student to know the difference order degree. Thisbetween is also the 2 ndand order polynomial.

Both sides are even functions. Cos (0) = 1 for both sides.

Both sides are odd functions. Sin (0) = 0 for both sides.

What is the interval of convergence for the sine series?

Find the Taylor Series for centered at a=1 And determine the interval of convergence

If the limit of the ratio between consecutive terms is less than one, then the series will converge.

If the limit of the ratio between consecutive terms is less than one, then the series will converge. The interval of convergence is (0, 2]. The radius of convergence is 1.

Power series for elementary functions Interval of Convergence