Aim How do we graph a linear system

Aim: How do we graph a linear system of inequalities? Do Now: Textbook Monitors distribute textbooks. Graph the inequality: y < 2 x - 3

Reminders • Quiz Friday, December 13 on: – finding a the equation of a line that is parallel to a given line – finding a the equation of a line that is perpendicular to a given line – Solving a system of linear equations graphically and algebraically • Test Tuesday, December 17

Page 382 # 11 y>5

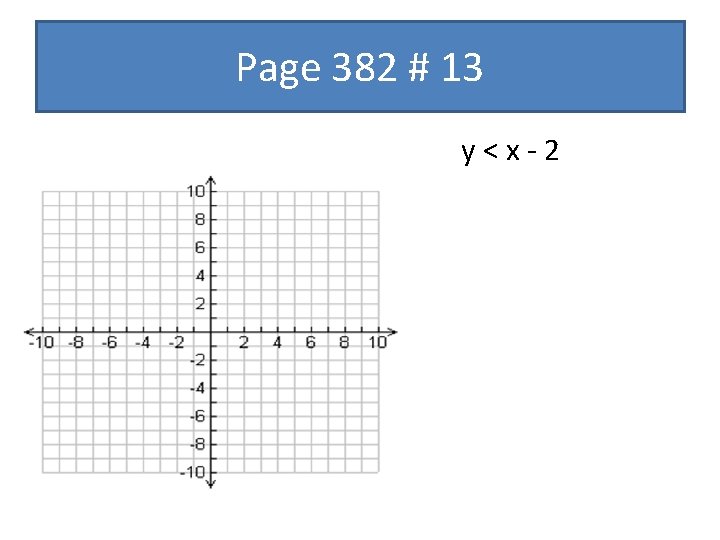
Page 382 # 13 y<x-2

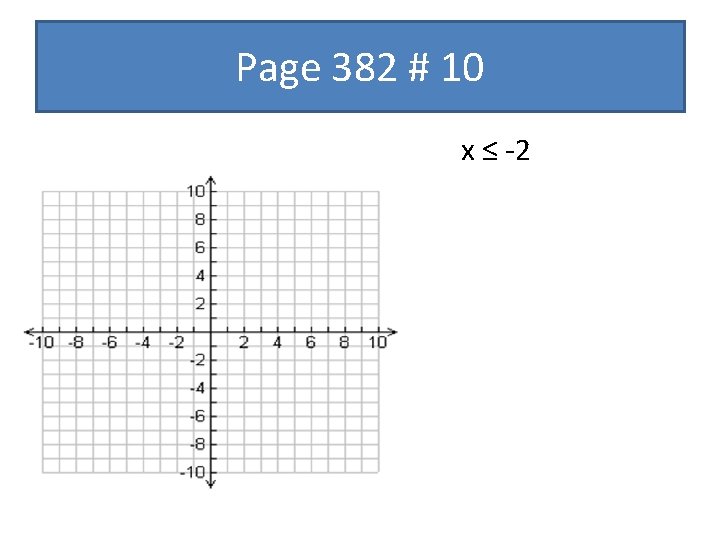
Page 382 # 10 x ≤ -2

Graphing a system of inequalities Procedure: 1) Graph each inequality separately. 2) The solution to the system, will be the area where the shadings from each inequality overlap one another.

Model Problem 1 Graph the solution set to this system. Label the solution set S: x>2 y < -2

Model Problem 2 Graph the solution set to this system. Label the solution set S: x+y≥ 4 y ≤ 2 x – 3

Together! Graph the solution set to this system. Label the solution set S: y < 2 x + 3 y>x

Aim: How do we graph a linear system of inequalities? Finish Practice time problems from yesterday! Page 434. Do # 12 -14 When you are done, notify Ms. Ryan!

Procedure for graphing inequalities 1. Solve the inequality for y (if necessary). 2. Graph the inequality as if it contained an equal sign 3. Dashed line or Bold line • • Bold for ≤, ≥ Dashed line for < , > 4. Pick a point NOT on the line to use as a test point. [(0, 0) is a good test point if not on the line. ] 5. Substitute the test point into the linear inequality. 6. If point makes the inequality true, shade that side of the line. If not, shade the other side

Practice time! You may work with a partner but you must be in your seat! In textbook, turn to page 434. Do # 6, 11 -14 • Before you ask for Ms. Ryan, TRY the following: – Think! – Check your notes. – Ask your classmate