Aim How can we solve graphing problems Answer

Aim: How can we solve graphing problems? Answer Key HW 1 Do Now: Combine: to form the formula d = vit + ½ at 2

The physical significance of the slope of a distance-time graph is average velocity!!! Positive velocity = forward Negative velocity = backward

No Calculator Allowed **1 minute** t 1. The displacement x of an object moving along the x‑axis is shown above as a function of time t. The acceleration of this object must be (A) zero (B) constant but not zero (C) increasing (D) decreasing (E) equal to g Constant slope=constant velocity =No acceleration

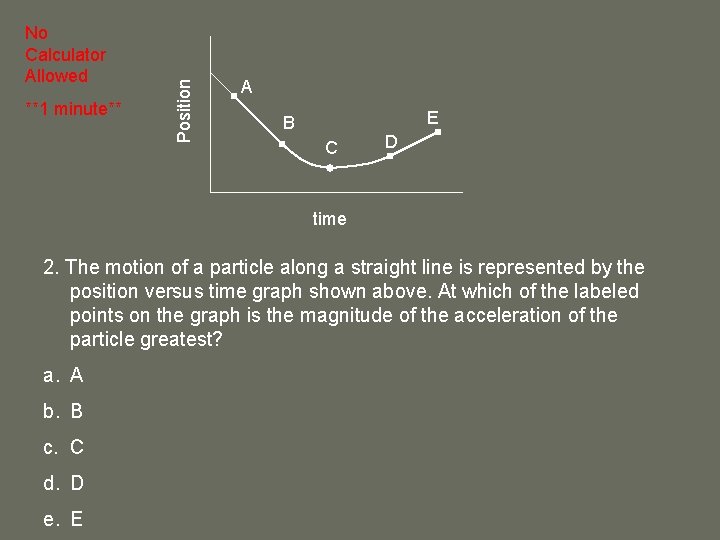
**1 minute** Position No Calculator Allowed A E B C D time 2. The motion of a particle along a straight line is represented by the position versus time graph shown above. At which of the labeled points on the graph is the magnitude of the acceleration of the particle greatest? b. B A, B, D, and E are all on straight lines c. C = constant slope a. A d. D e. E = constant velocity

3. A truck traveled 400 meters north in 80 seconds, and then it traveled 300 meters east in 70 seconds. The magnitude of the average velocity of the truck was most nearly No Calculator (A)1. 2 m/s Allowed (B)3. 3 m/s **1 minute** (C)4. 6 m/s (D)6. 6 m/s (E)9. 3 m/s

• The slope of a velocity-time graph is equal to the acceleration of the object (this is the physical significance of the slope) or • The area under the curve (the area between the line and the horizontal axis) is equal to: Øthe total distance traveled if you ignore the signs on the vertical axis Øthe total displacement of the object if you do not ignore the signs on the vertical axis

Describing acceleration by itself • Positive acceleration Increasing velocity; speeding up • Negative acceleration Decreasing velocity; slowing down

Describing acceleration and velocity together If velocity and acceleration are: • The same signs (+, +) or (-, -) ØThe object is speeding up • The opposite signs (+, -) or (-, +) ØThe object is slowing down

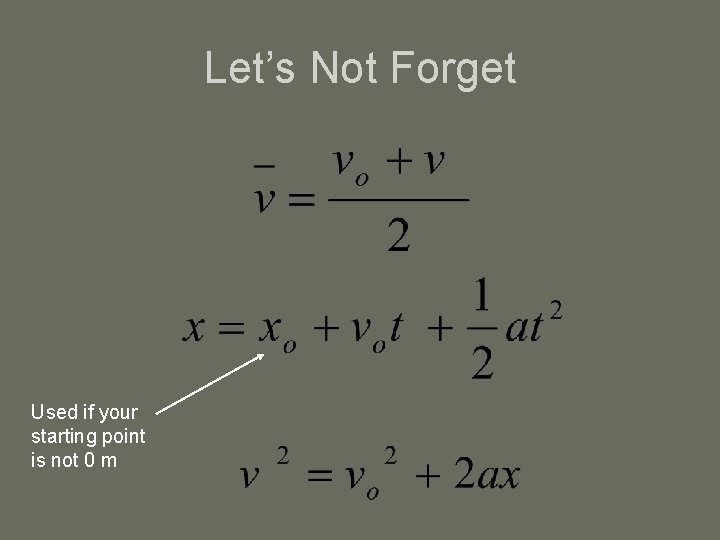
Let’s Not Forget Used if your starting point is not 0 m

4. An airplane accelerates uniformly from rest. The plane reaches a takeoff speed of 65 m/s after accelerating for a total of 30 s. Determine the minimum length of the runway needed. Calculator Allowed **2. 5 minutes to solve**

5. The first 10 meters of a 100‑meter dash are covered in 2 seconds by a sprinter who starts from rest and accelerates with a constant acceleration. The remaining 90 meters are run with the same velocity the sprinter had after 2 seconds. a. Determine the sprinter's constant acceleration during the first 2 seconds. b. Determine the sprinters velocity after 2 seconds have elapsed. c. Determine the total time needed to run the full 100 meters. d. On the axes provided below, draw the displacement vs time curve for the sprinter. Calculator Allowed **10 minutes to solve**

a. x = 10 m vo = 0 m/s x = vot + ½ at 2 x = ½ at 2 t=2 s 10 m = ½ (a)(2 s)2 a=? a = 5 m/s 2 b. v = vo + at v = (5 m/s 2)(2 s) v = 10 m/s

c. Find the velocity for 90 m Total time = 9 s + 2 s = 11 s

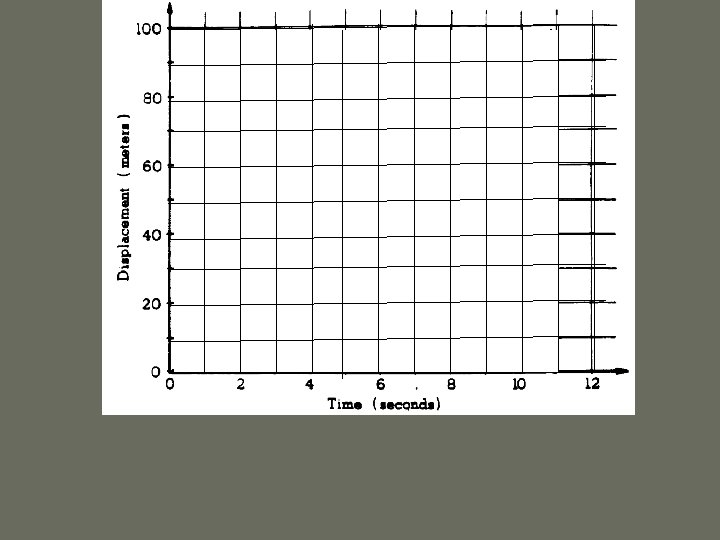
The object accelerates for the 1 st 2 s for 10 m = curved line The object maintains a const velocity for the next 9 s to 100 m = straight line

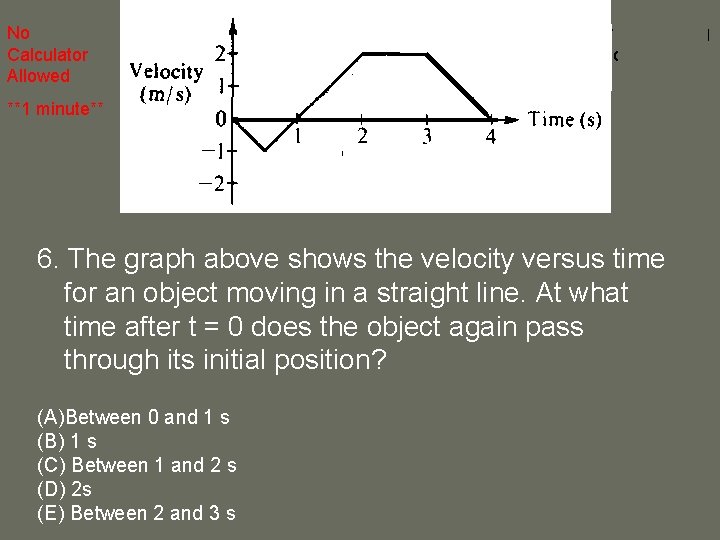
No Calculator Allowed Negative displacement A higher velocity would bring the object beyond its initial position **1 minute** This would yield 0 displacement 6. The graph above shows the velocity versus time for an object moving in a straight line. At what time after t = 0 does the object again pass through its initial position? (A)Between 0 and 1 s (B) 1 s (C) Between 1 and 2 s (D) 2 s (E) Between 2 and 3 s