Aim 4 8 What is Isometry Glide reflections

Aim 4. 8: What is Isometry, Glide reflections and point rotation? Do Now: Complete the following composition of transformations: T-3, 4 o R 90 degrees o r x-axis A ( 1, -2) B(3, -4) Homework: Packet pages 10 - 12 Test Friday

Aim 4. 8: What is Isometry, Glide reflections and point rotation? Homework Answers: Packet p. 1 1. a) (2, 4) (5, -1) (-5, -1) b) (-3, -4) (4, -3) (8, -6) Packet p. 2 5. b) A’ (-2, -2) B’ (-7, -4) C’ (-5, -6) c) A’’ (1, -6) B’’ (-4, -8) C’’ (-2, -10) 6. b) A’ (1, 3) B’ (3, 4) C’ (1, 6) c) A’’ (-3, 1) B’’ (-4, 3) C’’ (-6, 1) d) A’’’ (3, -1) B’’’ (4, -3) C’’’ (6, -1)

Aim 4. 8: What is Isometry, Glide reflections and point rotation? What is an Isometry? • Any transformation that preserves distance is a isometry • The only transformation that does NOT preserve isometry: Dilations • A direct isometry: any isometry that also preserves orientation. ▫ Translations & Dilations • An opposite isometry reverses orientation ▫ Reflections

Aim 4. 8: What is Isometry, Glide reflections and point rotation? What is a Glide Reflection? • Glide reflection: A translation and a reflection in the same composition. ▫ The line of reflection is parallel to the translation. ▫ Glide reflections are always compositions. ▫ Everything except orientation is preserved in a Glide reflection

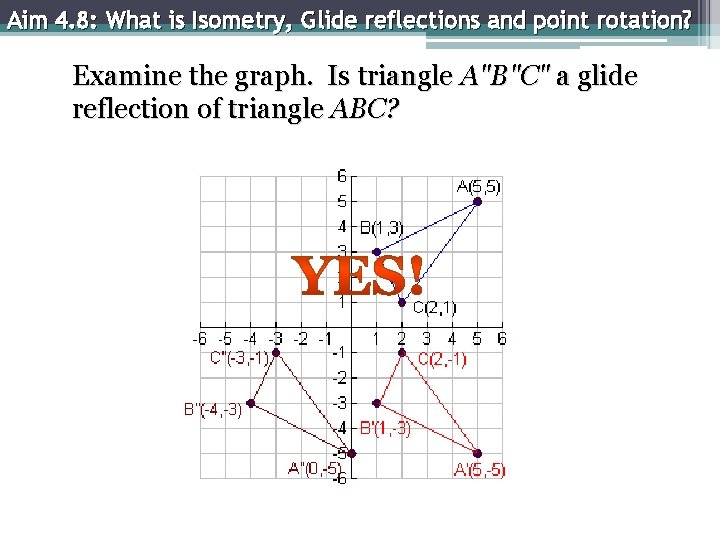
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Examine the graph. Is triangle A"B"C" a glide reflection of triangle ABC?

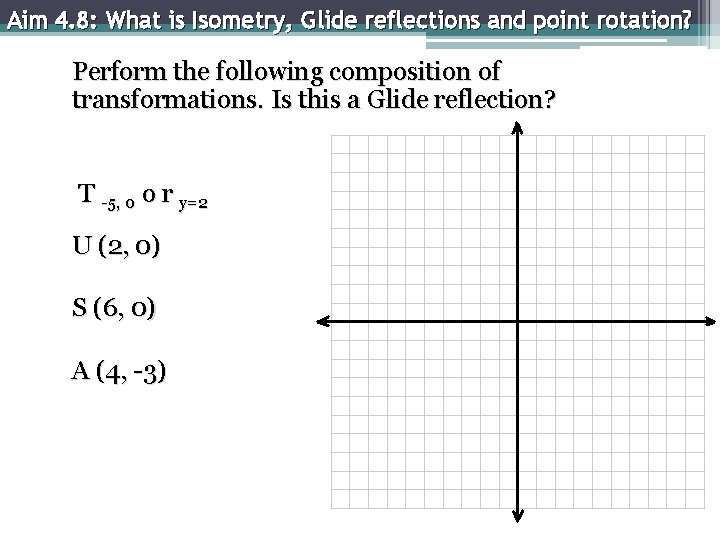
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Perform the following composition of transformations. Is this a Glide reflection? T -5, 0 o r y=2 U (2, 0) S (6, 0) A (4, -3)

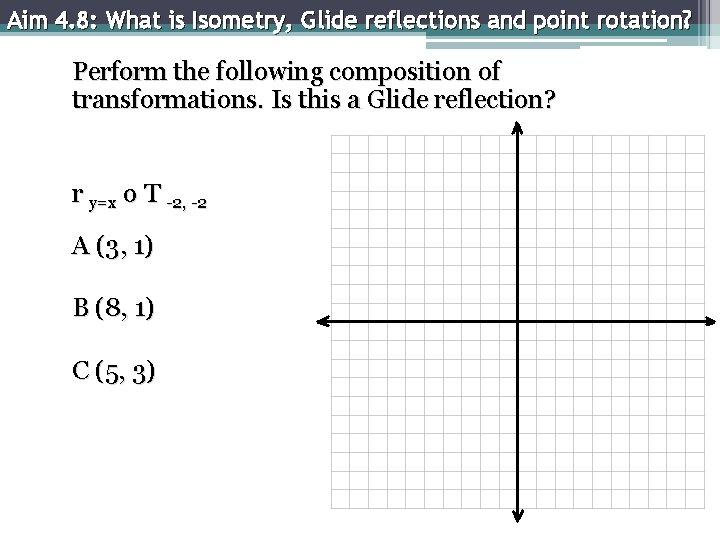
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Perform the following composition of transformations. Is this a Glide reflection? r y=x o T -2, -2 A (3, 1) B (8, 1) C (5, 3)

Aim 4. 8: What is Isometry, Glide reflections and point rotation? Work: r y=x o T -2, -2 A (3, 1) B (8, 1) C (5, 7) T -2, -2 A’ (1, -1) B’ (6, -1) C (3, 5) r y=x A’’ (-1, 1) B’’ (-1, 6) C’’ (5, 3)

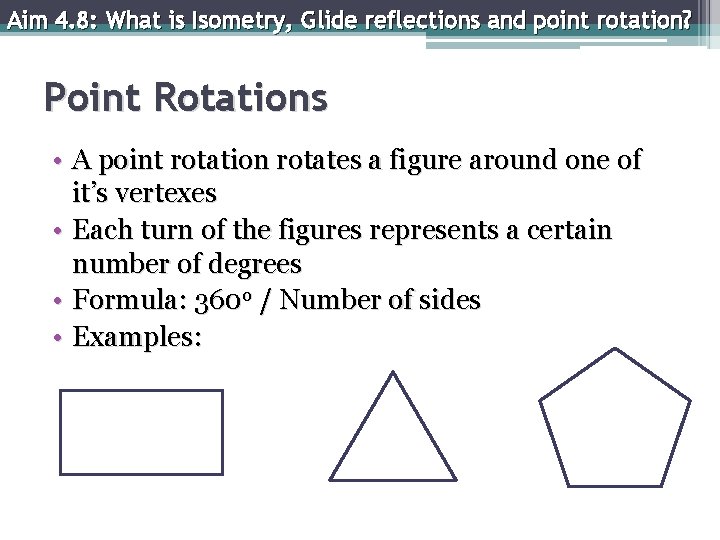
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Point Rotations • A point rotation rotates a figure around one of it’s vertexes • Each turn of the figures represents a certain number of degrees • Formula: 360 o / Number of sides • Examples:

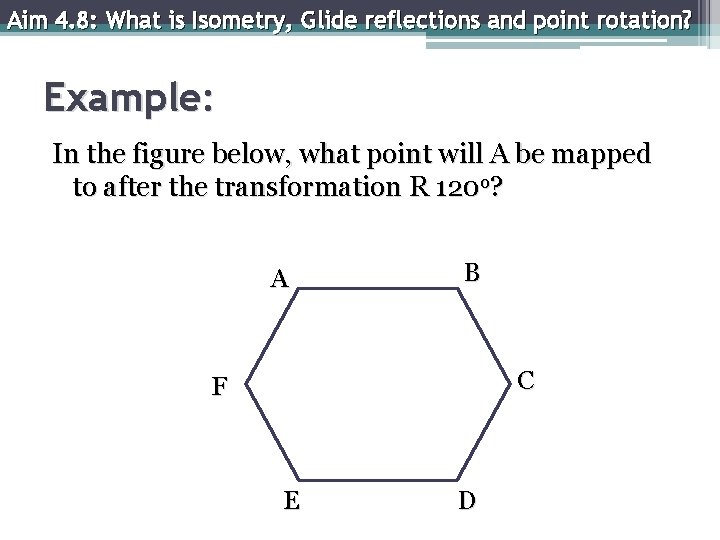
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Example: In the figure below, what point will A be mapped to after the transformation R 120 o? A B C F E D

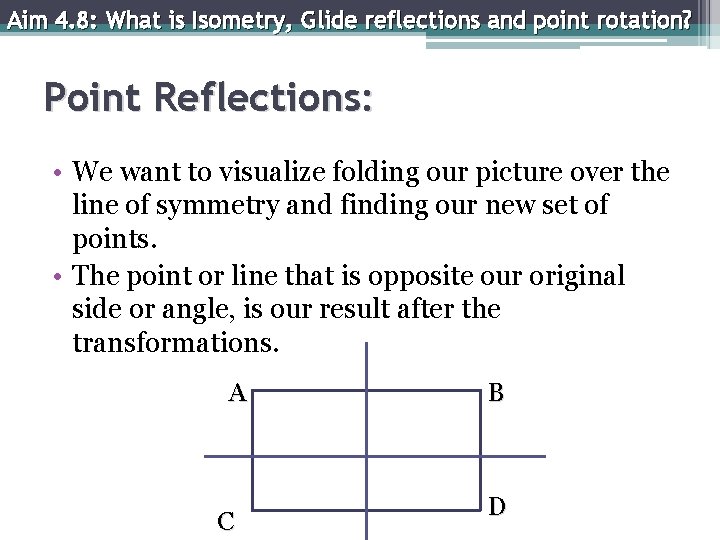
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Point Reflections: • We want to visualize folding our picture over the line of symmetry and finding our new set of points. • The point or line that is opposite our original side or angle, is our result after the transformations. A C B D

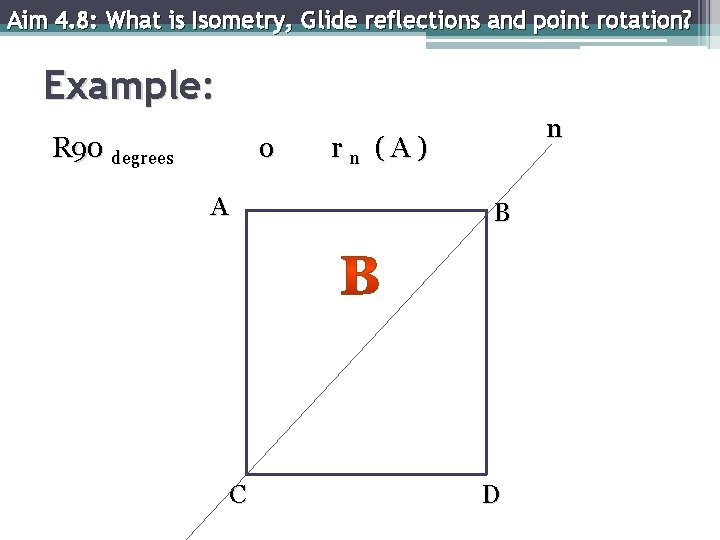
Aim 4. 8: What is Isometry, Glide reflections and point rotation? Example: R 90 degrees o A C n r n ( A ) B D

Aim 4. 8: What is Isometry, Glide reflections and point rotation? Exit Ticket: • Create an example of composition which is also a glide reflection. • Use this glide reflection on the point P (-2, 3) to determine point P’’