Aim 1 Chemistry Metrics Question How is the

Aim 1 – Chemistry Metrics Question: How is the metric system used in chem?

• Chemistry is: – the branch of science that deals with the _________ of which matter is composed; – the investigation of their properties and the ways in which they _________________ – and the use of these processes to ____________.

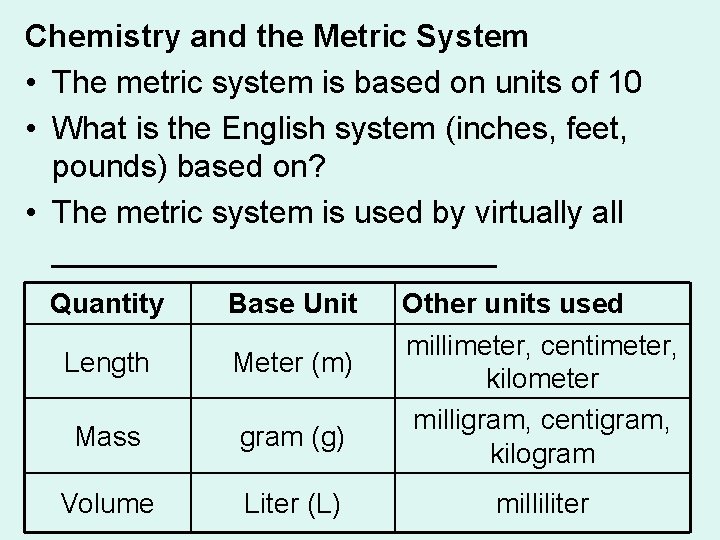
Chemistry and the Metric System • The metric system is based on units of 10 • What is the English system (inches, feet, pounds) based on? • The metric system is used by virtually all _____________ Quantity Base Unit Length Meter (m) Mass gram (g) Volume Liter (L) Other units used millimeter, centimeter, kilometer milligram, centigram, kilogram milliliter

Chemistry and the Metric System • Length – the measure of distance between two points – ____________ • Mass (def) - a measure of the _______ in an object in grams – 1 ounce = 28. 3 g and __________ • Mass is different from: – Weight (def) - the ___________ upon an object – measured in pounds – Volume (def) - the __________ an object takes up – measured in L or m. L

Converting metric units using prefixes • Why there are metric prefixes? – Measuring the volume of children’s Tylenol is easier in __________________ – Measuring the distance from NY to LA is more realistic in __________ – The dosage of acetaminophen in an aspirin tablet is easier to measure in _________________ • Prefixes simply change the size of the unit by increasing or decreasing the value by a _________________

Converting metric units using prefixes The prefixes you must memorize are as follows: • kilo = 1000 x the base unit • hecto = 100 x the base unit • deka = 10 x the base unit • base = grams, meters, liters, seconds, etc • deci = 1/10 x the base unit • centi = 1/100 x the base unit • milli = 1/1000 x the base unit • micro = 1/1, 000 x the base unit • pico = 1/1, 000, 000 x the base unit

Converting metric units using prefixes • Each prefix moves the decimal by a factor of 10 • MOVING DOWN the scale moves the decimal place to the ____________ by 10 • MOVING UP the scale moves the decimal place to the ____________ by 10 1 kilo = 10 hecto = 100 deka = 1, 000 base units 1 base unit = 10 deci = 100 centi = 1, 000 milli 1 base unit = 1, 000 (1 million) micro 1 base unit = 1, 000, 000 (1 billion) pico

Example: Convert 124 Converting metric units milligrams to grams. using prefixes 1. What is the conversion factor? The prefixes you must memorize are as follows: kilo = 1000 x hecto = 100 x deka = 10 x deci = 1/10 x centi = 1/100 x milli = 1/1000 x 2. What does the proportion look like for the conversion? 3. Solve for X:

Converting metric units using prefixes Example: Convert. 003 kilometers to meters. 1. What is the conversion factor? The prefixes you 2. What does the proportion look like for the conversion? must memorize are as follows: kilo = 1000 x hecto = 100 x deka = 10 x 3. Solve for X: deci = 1/10 x centi = 1/100 x milli = 1/1000 x

1. Convert 1. 2 kilometers to Practice in meters Metric 2. Convert 3. 4 grams to Conversion milligrams 3. Convert 1, 234 milliliters to The prefixes you liters must memorize 4. Convert 234 centimeters to are as follows: meters kilo = 1000 x 5. Convert 1. 0 deciliters to liters hecto = 100 x 6. Convert 0. 024 liters to deka = 10 x milliliters deci = 1/10 x 7. Convert 60 seconds to centi = 1/100 x milliseconds milli = 1/1000 x 8. Convert 1. 0 kilograms to milligrams

Hydrogen bomb blast over North Carolina, 1961

Aim 2 – Scientific Notation Question: How do scientists express large and small values in chemistry? 0. 00000289 = 2. 89 x 10 -11

Scientific notation - allows us to easily express large and small numbers • A number in scientific notation is written as follows: M x 10 n • M is the _______, 1< M < 10 • n is the _______– the number of 10’s we multiply or divide by – n can be an integer that is positive, negative, or 0 – If n is positive – multiply by 10’s – If n is negative – divide by 10’s – If n is zero (100) – multiply or divide by 1

Converting to scientific notation • Given the value: 6, 020 • To change this to scientific notation, we must determine the ___________ that will give us a mantissa that is 1 < M < 10 • 6. 02 is between 10 and 1 – We multiply 6. 02 by ______ – ___________ – to get 6, 020 – 1, 000 = 103 • Therefore, ________ is 6, 020 converted to scientific notation

Converting to scientific notation • Given the value: 0. 0000345 • To change this to scientific notation, we must by the number of 10’s that will give us a mantissa that is 1 < M < 10 • 3. 45 is between 10 and 1 – We divide 3. 45 by _______ or 10 x 10 to get 6, 020 – 1/100, 000 = 10 -5 • Therefore, ________ is 0. 0000345 converted to scientific notation

Converting scientific notation into numbers • For positive exponents: – Given the value: 7. 8 x 104 – To change the scientific notation into a number, simply multiply 7. 8 x 10 = _______ • For negative exponents: – Given the value: 4. 8 x 10 -4 – To change the scientific notation into a number simply divide 4. 8 / (10 x 10) = _______

Multiplying with scientific notation • When multiplying numbers: – ADD the exponents; – MULTIPLY the mantissas, – If need be, CHANGE the mantissa into a value between 0 and 1 • Examples a. (2. 0 x 105) x (8. 0 x 10 -2) = 16. 0 x 103 = 1. 60 x 103 b. (4. 0 x 104) x (5. 0 x 103) = 20 x 107 = 2. 0 x 108

Dividing with scientific notation • When dividing numbers: – SUBTRACT the exponents; – DIVIDE the mantissas, – If need be, CHANGE the mantissa into a value between 0 and 1 • Examples a. (6. 0 x 105) / (3. 0 x 10 -2) = 2. 0 x 107 b. (2. 0 x 106) / (5. 0 x 103) = 0. 4 x 103 = 4. 0 x 101

Adding and subtracting with sci notation • The exponents must be the same value • Example: – you cannot add 1. 2 x 103 and 2. 4 x 102 – You must convert the numbers so they ________________ • Examples a. (6. 0 x 102) + (3. 0 x 102) = 9. 0 x 102 b. (2. 0 x 103) + (5. 4 x 105) = (2. 0 x 103) + (540 x 103) = 542 x 103 = 5. 42 x 105

Practice in Scientific Notation 1. 2. 3. 4. 5. 6. 7. 8. Write in scientific notation: 0. 000467 Write in scientific notation: 32, 000 Express 5. 43 x 10 -3 as a number. Solve: (4. 5 x 10 -14) x (5. 2 x 103) = Solve: (6. 1 x 105)/(1. 2 x 10 -3) = Solve: (3. 74 x 10 -3) = Solve: (4. 4 x 102) + (6. 2 x 102) = Solve: (2. 4 x 103) – (8. 0 x 102) =

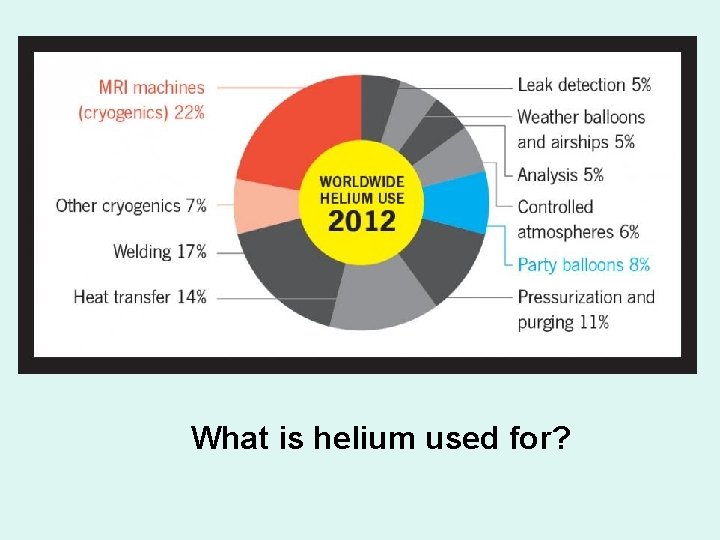
What is helium used for?

Aim 3 – Error in Chem Question: How do we determine the amount of accuracy in chemistry experiments? Hint: what makes Robin Hood the best with a bow?

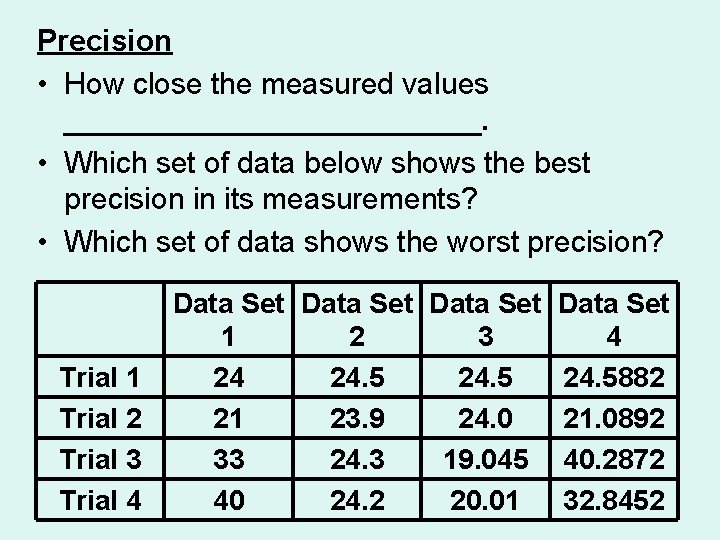
Precision • How close the measured values _____________. • Which set of data below shows the best precision in its measurements? • Which set of data shows the worst precision? Trial 1 Trial 2 Trial 3 Trial 4 Data Set 1 2 3 24 24. 5 21 23. 9 24. 0 33 24. 3 19. 045 40 24. 2 20. 01 Data Set 4 24. 5882 21. 0892 40. 2872 32. 8452

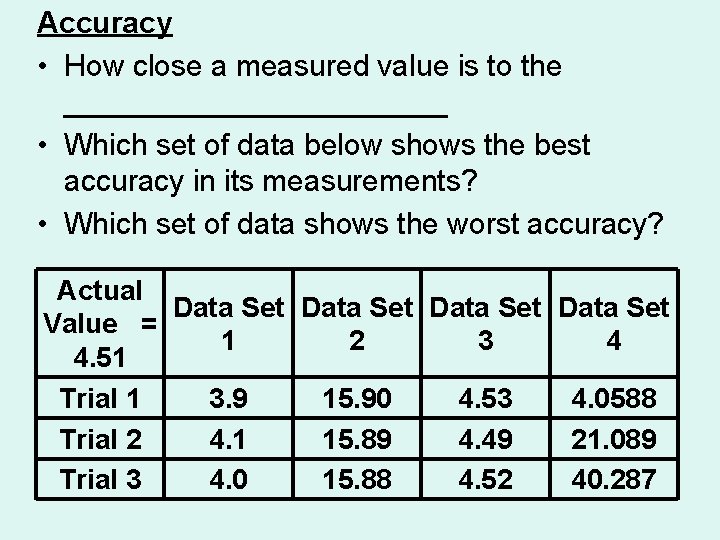
Accuracy • How close a measured value is to the ____________ • Which set of data below shows the best accuracy in its measurements? • Which set of data shows the worst accuracy? Actual Data Set Value = 1 2 3 4 4. 51 Trial 1 3. 9 15. 90 4. 53 4. 0588 Trial 2 4. 1 15. 89 4. 49 21. 089 Trial 3 4. 0 15. 88 4. 52 40. 287

Precision vs Accuracy • Chemistry measurements seek to have both _________________ • Some error does occur though; how do we determine the error in our measurements? • Table T – _____________

Percent Error in accuracy • To determine the percent error, use the following formula found on Table T: % error = Measured value – Accepted value x 100% Accepted value or % error = MV – AV x 100% AV • ___________ – what the student, scientist, or experiment determines as a value • ___________ – theoretical, actual, real, or true value

Percent Error in accuracy • Example 1: A student determines the density of a metal sample to be 3. 4 g/m. L. The accepted value for the density is 3. 0 g/m. L. What is the percent error in the student’s measurement? % error = MV – AV x 100% AV % error =

Percent Error in accuracy • Example 2: A researcher makes an error collecting a gas in his experiment. He collected only 605 m. L of gas instead of theoretical yield of 650 m. L. What is his percent error? % error = MV – AV x 100% AV % error =

Practice – Error in Measurements 1. How much error is in an experiment where the measured value is 10. 0 m. L but the accepted value is 9. 0 m. L? 2. A gum manufacturer uses his latest supply of gum ingredients to make 5, 900 pieces of gum. He was actually supposed to make 6, 000 pieces of gum. What is the percent error in his gum yield? 3. The accepted value for a chemical’s boiling point is 1, 200 o. C. A scientist determines experimentally that the boiling point is 1, 150 o. C. What is his percent error?

Aim 4 – Significant Figures Question: How can we show precision our measurements are?

Significant figures • the number of significant figures in a result is simply the number of figures that are known with some ____________. • Example: – The number 13. 2 is said to have 3 significant figures. – The number 13. 20 is said to have 4 significant figures. • Significant figures allow us to show the level of __________ in measurement

Real World examples: • A manufacturer claims each pack of their lollipops contains 20 lollipops. • Accuracy: – a sample of packets have 19, 20, 22, 18, 21, 19, 21 lollipops. – The average is 20. – _________________ • Precision: – a sample of packets have 18, 17, 17, 18, 17 lollipops. – The claim is not accurate, but the number of lollipops in each bag _________

Real World examples: • While doing an experimental test in chemistry with five trials, the end results of the five trials the test are: 35 kg, 36 kg, 33 kg, 35 kg, 36 kg. The actual value (as found in a scientific data book) is meant to be 42 kg. – From the results, __________ – _________ since the actual value should be 42 kg. – _________, since they do not vary from each other.

Rules for determining significant figures 1) ALL non-zero numbers (1, 2, 3, 4, 5, 6, 7, 8, 9) are ALWAYS significant. – 1. 456 4 significant figures – 2, 298, 356 7 significant figures – 1, 234. 58 6 significant figures 2) ALL zeroes between non-zero numbers are ALWAYS significant. – 1. 001 4 significant figures – 2, 200. 4 5 significant figures – 101 3 significant figures

Rules for determining significant figures 3) ALL zeroes which are SIMULTANEOUSLY to the right of the decimal point AND at the end of the number are ALWAYS significant. – 1. 00 3 significant figures – 1. 00400 6 significant figures 4) ALL zeroes which are to the left of a written decimal point and are in a number > 10 are ALWAYS significant. – 1, 000 1 significant figure – 410 2 significant figures

Rules for determining significant figures • A helpful way to check rules 3 and 4 is to write the number in scientific notation. • If you can/must get rid of the zeroes, then they are NOT significant. • Examples: How many significant figures are present in the following numbers? – 1, 010 3 significant figures – 0. 00040 2 significant figures – 12, 000 2 significant figures – 100. 0 4 significant figures

What is an "exact number"? • Some numbers are exact because they are known with complete certainty. • Most exact numbers are integers: – exactly _____________________ – Exact numbers are often found as conversion factors or as counts of objects. • Exact numbers can be considered to have an __________________ • The number of apparent significant figures in any exact number can be ignored as a limiting factor in determining the number of significant figures in the ________________

Reporting measured quantities In Summary 1. All non zero numbers are significant (1 -9) 2. Zeros located between non zero numbers are significant 3. Zeros used to place other numbers ARE NOT significant figures 4. Zeros at the end of a number that contains a decimal ARE significant

Aim 5: How do we calculate using significant figures? Or, why Mr. Foley does not build bridges anymore Darn it! I told Foley to round to the 1, 000 th place, not the 10 th!!!!

Calculations with Significant Figures • When calculating using multiplication and division: – Answers can only have as many significant figures as the number with the least number of significant figures • Ex 1. 4, 040 How many sig figs? 3 x 20. How many sig figs? 2 = How many in answer? 3 = How many sig figs should be in the answer? 2

Calculations with Significant Figures • Ex 2. 1, 040 How many sig figs? 3 x 10. 41 How many sig figs? 4 = How many in answer? 6 = How many sig figs should be in the answer? 3 • Ex 3. 25, 000. 0 How many sig figs? 6 125 How many sig figs? 3 = How many in answer? 1 = How many sig figs should be in the answer? 3

Calculations with Significant Figures • Addition and Subtraction: – Answer can have as many decimals as the least number in the problem. Ex 1 40. 108 + 2. 3 42. 408 42. 4 Ex 2 5, 250. 4 - 250. 355 5, 000. 545 5, 000. 5

Practice Calculations with Sig Figs a) 2. 34 x 12, 000 = 28, 000 b) 1. 5 / 678 = 0. 0022 c) 41. 25 + 0. 008 = 41. 26 d) 41. 25 – 1. 2 = 40. e) 0. 500 – 0. 23 = 0. 27 f) 125, 000 x 23 = 2, 900, 000 g) 34, 000. 0 / 23 = 1, 500 h) 1. 23 + 0. 1004 = 1. 33