AGIs EAP Curriculum Orbital Mechanics Lesson 1 Orbital

AGI’s EAP Curriculum Orbital Mechanics Lesson 1 - Orbital Elements

Introduction § This powerpoint was designed to aid professors in teaching several concepts for an introductory orbital mechanics class. The powerpoint incorporates visuals from Systems Tool Kit (STK) that help students better understand important concepts. § Any relevant parts of the powerpoint (images, videos, scenarios, etc) can be extracted and used independently. § At the end of each lesson there are optional example problems and a tutorial that further expands upon the lesson. Students can complete these as part of a lab or homework assignment. § Here is the link to download all of the supporting scenarios: EAP Scenarios – Username: anonymous Password: (leave blank)

Lesson 1: Orbital Elements § Lesson Overview – – – What is an Orbit? Kepler’s Laws 6 orbital elements Ground Tracks Coordinate Frames & Epoch

What is an Orbit? An orbit is a closed “path” around which a planet or satellite travels. In the simplest sense, orbits are a type of "racetrack" in space that a satellite "drives" around. How fast would a car have to “drive” to stay in orbit? Remember from your physics class, the centripetal acceleration of a car around a circular track is: a = v 2/r And the force of gravity is: 1) F = GMm/r 2 = ma 2) F/m=a = GM/r 2 3) GM/r 2 = v 2/r 4) v = √(GM/r) So for a “car” at a 9, 000 km altitude (as shown): G = 6. 674 x 10 -11 m 3 kg-1 s-2 Mearth = 5. 972 x 1024 kg rcar=rearth+raltitude= 6, 378. 14+9, 000 km=15, 378. 14 km v = √(GM/r) = 5. 09 km/s !!!! Lower altitude orbits travel even faster! There are many different types of orbits which are described by various orbital elements. Before jumping into specific orbits we will cover Kepler’s 3 laws of orbital motion.

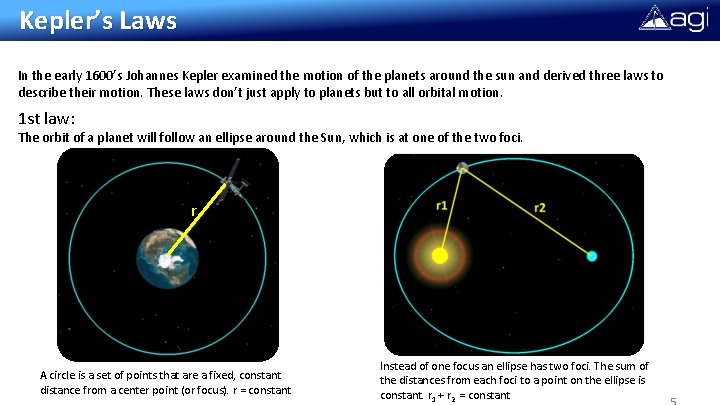
Kepler’s Laws In the early 1600’s Johannes Kepler examined the motion of the planets around the sun and derived three laws to describe their motion. These laws don’t just apply to planets but to all orbital motion. 1 st law: The orbit of a planet will follow an ellipse around the Sun, which is at one of the two foci. r A circle is a set of points that are a fixed, constant distance from a center point (or focus). r = constant Instead of one focus an ellipse has two foci. The sum of the distances from each foci to a point on the ellipse is constant. r 1 + r 2 = constant

Kepler’s Laws 2 nd law: A line joining a planet and the Sun sweeps out equal areas during equal intervals of time. The same is true for satellites around the planets. The area swept out is equal for equal time. This implies that the satellite moves faster when closer to Earth and slower when further away from Earth. A 1 A 2 A 1 = A 2 Video: Kepler’s 2 nd Law

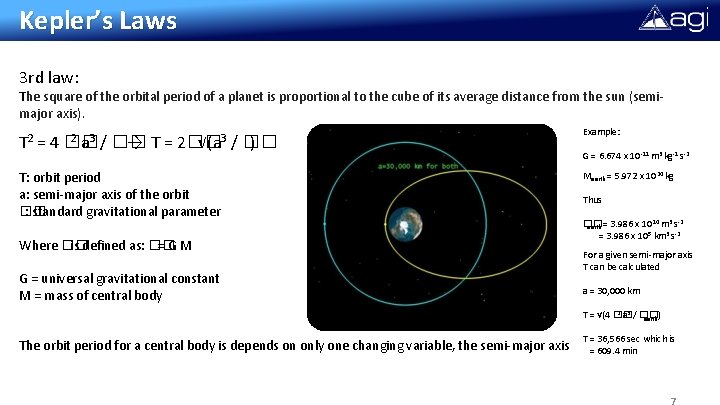
Kepler’s Laws 3 rd law: The square of the orbital period of a planet is proportional to the cube of its average distance from the sun (semimajor axis). 2 a 3 / �� T 2 = 4 �� → T = 2�� √(a 3 / �� ) T: orbit period a: semi-major axis of the orbit �� : standard gravitational parameter Where �� is defined as: �� =GM G = universal gravitational constant M = mass of central body Example: G = 6. 674 x 10 -11 m 3 kg-1 s-2 Mearth = 5. 972 x 10 24 kg Thus 14 3 -2 �� earth = 3. 986 x 10 m s 5 = 3. 986 x 10 km 3 s-2 For a given semi-major axis T can be calculated a = 30, 000 km 2 a 3 / ��) T = √(4 �� earth The orbit period for a central body is depends on only one changing variable, the semi-major axis T = 36, 566 sec which is = 609. 4 min

Coordinate System & Epoch All orbital elements need to be defined in a Coordinate System and at an epoch (specified time). Coordinate System A reference axes with a specified origin Commonly Earth Centered Inertial (ECI): The reference plane is typically the Earth’s equatorial plane. The x direction is fixed relative to the celestial sphere. The vernal equinox is used as the reference direction. The y direction is 90 degrees from the x axis within the equatorial plane. The z direction is pointed upward from the north pole. Epoch, Commonly J 2000 A reference time, or a timestamp, in which time varying celestial data is defined. A commonly used epoch is J 2000 January 1, 2000 at 11: 58: 56 GMT

Orbital Elements Now that we know what type of motion the planets follow. . . How do we define properties of an orbit? To fully define the instantaneous trajectory of a planet or satellite we need 6 parameters. In cartesian coordinates: 3 parameters for position • • • X Y Z and 3 parameters for velocity • • • Vx Vy Vz However, there is a more convenient set of parameters which allows us to utilize Kepler’s laws to predict the position and velocity of the orbiting body, both instantaneously and in the future.

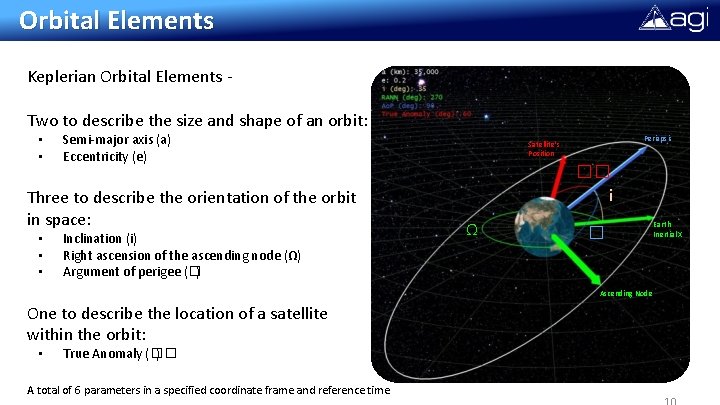
Orbital Elements Keplerian Orbital Elements Two to describe the size and shape of an orbit: • • Semi-major axis (a) Eccentricity (e) Three to describe the orientation of the orbit in space: • • • Inclination (i) Right ascension of the ascending node (Ω) Argument of perigee (�) Periapsis Satellite’s Position �� i Ω � Ascending Node One to describe the location of a satellite within the orbit: • True Anomaly (�� ) A total of 6 parameters in a specified coordinate frame and reference time Earth Inertial X

Orbital Elements Semi-major axis (a): Semi-major axis describes the size of the ellipse. It is half of the largest diameter (the major axis) of the orbit. Video: Semi-major Axis Download Scenario: Semi-major axis Username: anonymous Password: (leave blank)

Orbital Elements Semi-major axis (a): Periapsis - The point in an orbit that is closest to the central body. Apoapsis - The point in an orbit that is farthest from central body. rp is distance from center of the central body to periapsis ra is distance from center of the central body to apoapsis 2 a =(ra+rp) → a = (ra + rp) / 2 Note: Instead of the suffix -apsis, the suffix -gee is used for objects specifically orbiting the Earth. Thus they are known as Perigee and Apogee. ra Center of Central Body rp

Orbital Elements Eccentricity (e): Eccentricity describes the “roundness” of an orbit. It is a ratio between the semi-minor axis and semi-major axis of an orbit. A “perfect” circular orbit has an eccentricity value of 0. The more eccentric the orbit (as e↑), the less circular the orbit. Video: Eccentricity Download Scenario: Eccentricity

Orbital Elements Eccentricity (e): An orbit is a trajectory with an e value less than 1 because an orbit is a closed path around a central body. A trajectory with an eccentricity greater than or equal to 1 is an open trajectory, and the “orbiting” body will constantly move away from the central body. For orbits or closed trajectories: 0 ≤ e < 1 • Circle: e = 0 • Ellipse: 0 < e < 1 For open trajectories: e ≥ 1 • Parabola: e = 1 • Hyperbola: e > 1

Orbital Elements Inclination (i): Inclination is the angle between the Earth’s equatorial plane and the plane of the orbit. It describes the “tilt” of the orbit. A higher inclination will cover higher latitude values. To the right is a ground track. It is the projection of the satellite’s orbit onto Earth's surface. Ground tracks vary based on the satellite’s orbital elements which define its motion. The inclination can be determined by observing the satellite’s ground track. The latitude of the point furthest from the equator determines the satellite’s inclination. Download Scenario: Inclination Video: Inclination

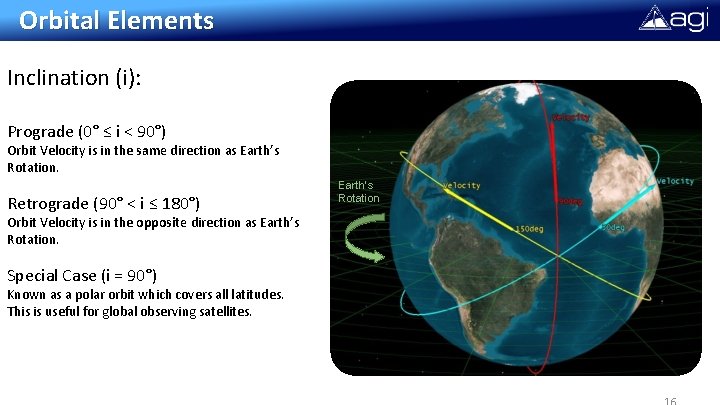
Orbital Elements Inclination (i): Prograde (0° ≤ i < 90°) Orbit Velocity is in the same direction as Earth’s Rotation. Retrograde (90° < i ≤ 180°) Orbit Velocity is in the opposite direction as Earth’s Rotation. Special Case (i = 90°) Known as a polar orbit which covers all latitudes. This is useful for global observing satellites. Earth’s Rotation

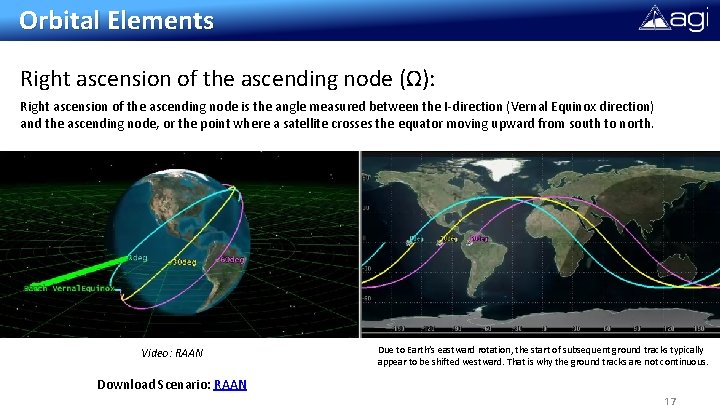
Orbital Elements Right ascension of the ascending node (Ω): Right ascension of the ascending node is the angle measured between the I-direction (Vernal Equinox direction) and the ascending node, or the point where a satellite crosses the equator moving upward from south to north. Video: RAAN Download Scenario: RAAN Due to Earth’s eastward rotation, the start of subsequent ground tracks typically appear to be shifted westward. That is why the ground tracks are not continuous.

Orbital Elements Argument of perigee (ω): The argument of perigee is the angle between the ascending node and the periapsis point of the orbit. Video: Argument of Perigee Download Scenario: Argument of Perigee

Orbital Elements True Anomaly (�� ): True Anomaly is the angle between periapsis and the satellite’s current position measured from the center of the central body. This is the only orbital element that changes with respect to time. Video: True Anomaly Download Scenario: True Anomaly

Orbital Elements Summary of Orbital Elements: Name Symbol Describes Semi-major axis a Orbit size Eccentricity e Orbit shape Inclination i Tilt of orbit plane relative to the equator Right ascension of the Ascending Node Ω Twist of ascending node from the reference direction Argument of Perigee ω Location of periapsis relative to the ascending node True Anomaly �� Periapsis Satellite’s Position �� i Ω � Earth Inertial X Ascending Node Location of satellite relative to periapsis Download Scenario: Orbital Elements 20

End Lesson 1 - Tutorial Orbit Wizard: The Orbit Wizard is an excellent plugin tool that can be used to quickly adjust and visualize orbital elements. This plugin works with STK 11 and can be downloaded here for free. Download tutorial to further explore using Orbit Wizard: Lesson 1 Tutorial Video: Orbit Wizard

End Lesson 1 - Exercises True or False: 1. T / F Perigee describes the point in an orbit closest to earth. 2. T / F A circular orbit has an apogee exactly twice the altitude of its perigee. 3. T / F The right ascension of the ascending node is defined from the point where a satellite crosses the prime meridian. Short Answer: 4. How many parameters does the Keplerian element set consist of? What are they? 5. What eccentricity value does a perfect circle have? 6. What is/are the orbital element(s) which constantly change throughout a satellite’s orbit? 7. A satellite designed to take images to monitor the polar ice caps would have an inclination close to what value(deg )?

End Lesson 1 - Answers True or False: 1. T / F Perigee describes the point in an orbit closest to earth. 2. T / F A circular orbit has an apogee exactly twice the altitude of its perigee. 3. T / F The right ascension of the ascending node is defined from the point where a satellite crosses the prime meridian. Short Answer: 4. How many parameters does the Keplerian element set consist of? What are they? Six - They are semi-major axis, eccentricity, inclination, argument of perigee, RAAN, and true anomaly. 5. What eccentricity value does a perfect circle have? e=0 6. What is/are the orbital element(s) which constantly change throughout a satellite’s orbit? True anomaly 7. A satellite designed to take images to monitor the polar ice caps would have an inclination close to what value(deg )? 90 degrees

Additional Resources § STK Data Federate link for scenario vdf’s: EAP Scenarios – Username: anonymous Password: (leave blank) § Check out related additional scenarios: – Flight Path Angle – Eccentric Anomaly – Mean Anomaly § Visit AGI. com/edu to learn more about the available curriculum and the Educational Alliance Program (EAP) § To learn more about STK: – Beginner-level video tutorials – Complete STK Certification § Questions / Comments: – Education@agi. com