Aggregate Function Computation and Iceberg Querying in Vertical

Aggregate Function Computation and Iceberg Querying in Vertical Databases Yue (Jenny) Cui and William Perrizo North Dakota State University

Outline o Introduction n n o Algorithms of Aggregate Function Computation Using P-trees n n o o Review of Aggregate Functions Review P-tree vertical, compressed dataminingready data structures SUM, COUNT, and AVERAGE. MAX, MIN, MEDIAN, RANK, and TOP-K. Performance Analysis Conclusion

Introduction o o o Commonly used aggregation functions include COUNT, SUM, AVERAGE, MIN, MAX, MEDIAN, RANK, and TOP-K. Iceberg queries perform aggregate functions across attributes and then eliminate aggregate values that are below some specified threshold. example iceberg query. SELECT FROM GROUPBY HAVING Location, Product Type, Sum (# Product) Relation Sales Location, Product Type Sum (# Product) >= T

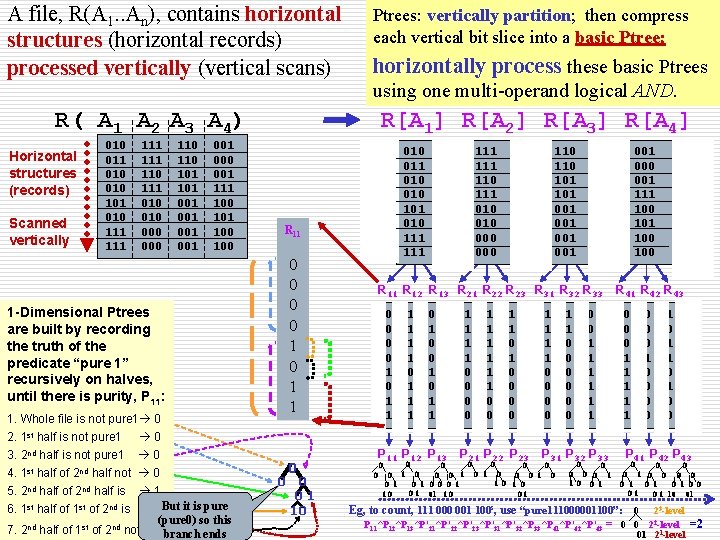
A file, R(A 1. . An), contains horizontal structures (horizontal records) processed vertically (vertical scans) Ptrees: vertically partition; then compress each vertical bit slice into a basic Ptree; horizontally process these basic Ptrees using one multi-operand logical AND. R( A 1 A 2 A 3 A 4) Horizontal structures (records) Scanned vertically 010 011 010 101 010 111 111 110 111 010 000 110 101 001 001 001 000 001 111 100 100 R[A 1] R[A 2] R[A 3] R[A 4] R 11 0 0 1 0 1 1 1 -Dimensional Ptrees are built by recording the truth of the predicate “pure 1” recursively on halves, until there is purity, P 11: 1. Whole file is not pure 1 0 2. 1 st half is not pure 1 0 3. 2 nd half is not pure 1 0 4. 1 st half of 2 nd half not 0 5. 2 nd half of 2 nd half is 1 6. 1 st half of 1 st of 2 nd is 1 But it is pure (pure 0) so this 7. 2 nd half of 1 st of 2 nd not 0 branch ends 010 011 010 101 010 111 0 01 1 10 111 110 111 010 000 110 101 001 001 001 000 001 111 100 100 R 11 R 12 R 13 R 21 R 22 R 23 R 31 R 32 R 33 0 0 1 0 1 1 1 0 0 1 1 1 0 0 1 1 0 0 0 0 1 1 1 R 41 R 42 R 43 0 0 0 1 1 1 0 0 0 0 1 1 0 0 P 11 P 12 P 13 P 21 P 22 P 23 P 31 P 32 P 33 P 41 P 42 P 43 0 0 0 0 1 0 0 01 0 0 0 10 10 10 01 01 0001 0100 01 01 10 Eg, to count, 111 000 001 100 s, use “pure 111000001100”: 0 23 -level P 11^P 12^P 13^P’ 21^P’ 22^P’ 23^P’ 31^P’ 32^P 33^P 41^P’ 42^P’ 43 = 0 0 22 -level =2 01 21 -level

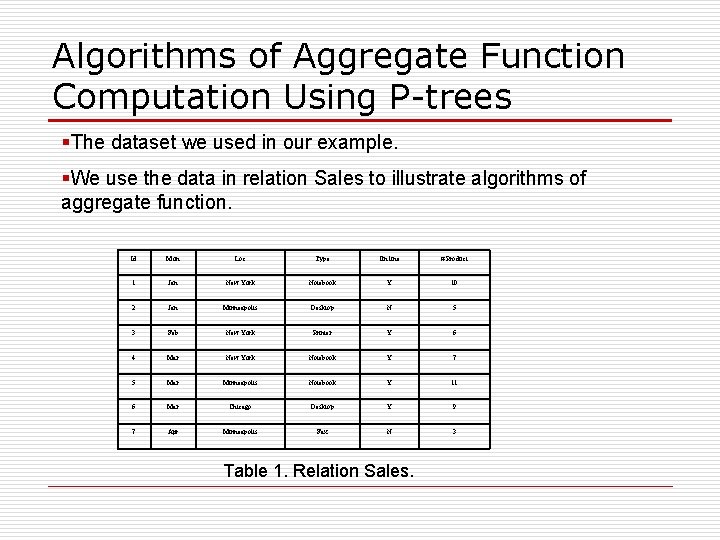
Algorithms of Aggregate Function Computation Using P-trees §The dataset we used in our example. §We use the data in relation Sales to illustrate algorithms of aggregate function. Id Mon Loc Type On line # Product 1 Jan New York Notebook Y 10 2 Jan Minneapolis Desktop N 5 3 Feb New York Printer Y 6 4 Mar New York Notebook Y 7 5 Mar Minneapolis Notebook Y 11 6 Mar Chicago Desktop Y 9 7 Apr Minneapolis Fax N 3 Table 1. Relation Sales.

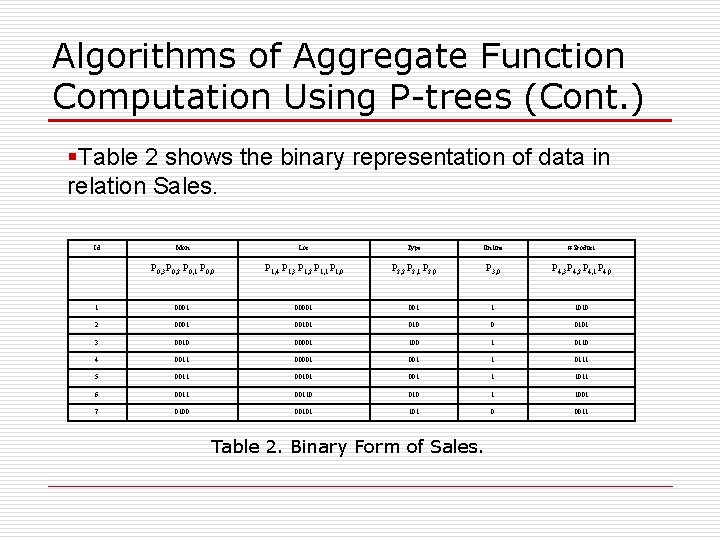
Algorithms of Aggregate Function Computation Using P-trees (Cont. ) §Table 2 shows the binary representation of data in relation Sales. Id Mon Loc Type On line # Product P 0, 3 P 0, 2 P 0, 1 P 0, 0 P 1, 4 P 1, 3 P 1, 2 P 1, 1 P 1, 0 P 2, 2 P 2, 1 P 2, 0 P 3, 0 P 4, 3 P 4, 2 P 4, 1 P 4, 0 1 00001 001 1 1010 2 0001 00101 010 0 0101 3 0010 00001 100 1 0110 4 0011 00001 1 0111 5 0011 00101 001 1 1011 6 00110 010 1 1001 7 0100 00101 0 0011 Table 2. Binary Form of Sales.

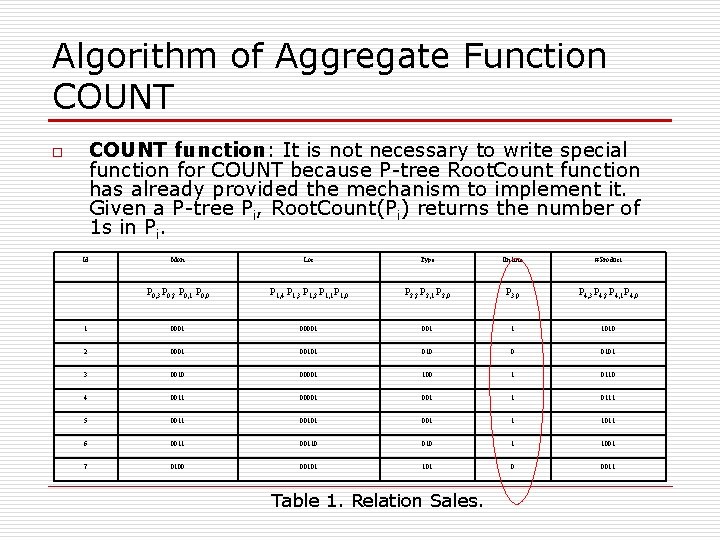
Algorithm of Aggregate Function COUNT function: It is not necessary to write special function for COUNT because P-tree Root. Count function has already provided the mechanism to implement it. Given a P-tree Pi, Root. Count(Pi) returns the number of 1 s in Pi. o Id Mon Loc Type On line # Product P 0, 3 P 0, 2 P 0, 1 P 0, 0 P 1, 4 P 1, 3 P 1, 2 P 1, 1 P 1, 0 P 2, 2 P 2, 1 P 2, 0 P 3, 0 P 4, 3 P 4, 2 P 4, 1 P 4, 0 1 00001 001 1 1010 2 0001 00101 010 0 0101 3 0010 00001 100 1 0110 4 0011 00001 1 0111 5 0011 00101 001 1 1011 6 00110 010 1 1001 7 0100 00101 0 0011 Table 1. Relation Sales.

Algorithm of Aggregate Function SUM o SUM function: Sum function can total a field of numerical values. Algorithm 4. 1 Evaluating sum () with P-tree. total = 0. 00; For i = 0 to n { total = total + 2 i * Root. Count (Pi); } Return total Algorithm 4. 1. Sum Aggregate

Algorithm of Aggregate Function SUM P 4, 3 P 4, 2 P 4, 1 P 4, 0 10 1 0 5 0 1 6 0 1 1 0 7 0 1 11 1 0 1 1 9 1 0 0 1 3 0 0 1 1 {3} {5} 23 * + 22 * + 21 * + 20 * §For example, if we want to know the total number of products which were sold out in relation Sales, the procedure is showed on left = 51

Algorithm of Aggregate Function AVERAGE o Average function: Average function will show the average value in a field. It can be calculated from function COUNT and SUM. Average () = Sum ()/Count ().

Algorithm of Aggregate Function MAX o Max function: Max function returns the largest value in a field. Algorithm 4. 2 Evaluating max () with P-tree. max = 0. 00; c = 0; Pc is set all 1 s For i = n to 0 { c = Root. Count (Pc AND Pi); If (c >= 1) Pc = Pc AND Pi; max = max + 2 i; } Return max; Algorithm 4. 2. Max Aggregate.

Algorithm of Aggregate Function MAX P 4, 3 P 4, 2 P 4, 1 P 4, 0 10 1 0 5 0 1 6 0 1 1 0 7 0 1 11 1 0 1 1 9 1 0 0 1 3 0 0 1 1 Steps IF Pos Bits >= 1 {1} 1 {0} 1 {1} 4. Root. Count (Pc AND P 4, 0 ) = 1 >= 1 {1} 1. Pc = P 4, 3 Root. Count (Pc) = 3 2. Root. Count (Pc AND P 4, 2) = 0 < Pc = Pc AND P’ 4, 2 3. Root. Count (Pc AND P 4, 1 ) = 2 >= Pc AND P 4, 1 23 * {1}+ 22 *{0}+ 21 * {1}+ 20 * {1} = 11

Algorithm of Aggregate Function MIN o Min function: Min function returns the smallest value in a field. Algorithm 4. 3. Evaluating Min () with P-tree. min = 0. 00; c = 0; Pc is set all 1 s For i = n to 0 { c = Root. Count (Pc AND NOT (Pi)); If (c >= 1) Pc = Pc AND NOT (Pi); Else min = min + 2 i; } Return min; Algorithm 4. 2. Max Aggregate.

Algorithm of Aggregate Function MIN P 4, 3 P 4, 2 P 4, 1 P 4, 0 10 1 0 5 0 1 6 0 1 1 0 7 0 1 11 1 0 1 1 9 1 0 0 1 3 0 0 1 1 Steps IF Pos Bits 1. Pc = P’ 4, 3 >= 1 {0} 2. Root. Count (Pc AND P’ 4, 2) = 1 >= 1 {0} Root. Count (Pc) = 4 Pc = Pc AND P’ 4, 2 3. Root. Count (Pc AND P’ 4, 1 ) = 0 < 1 {1} Pc = Pc AND P 4, 1 4. Root. Count (Pc AND P’ 4, 0 ) = 0 < 1 23 * {0}+ 22 *{0}+ 21 * {1}+ 20 * {1} = 3 {1}

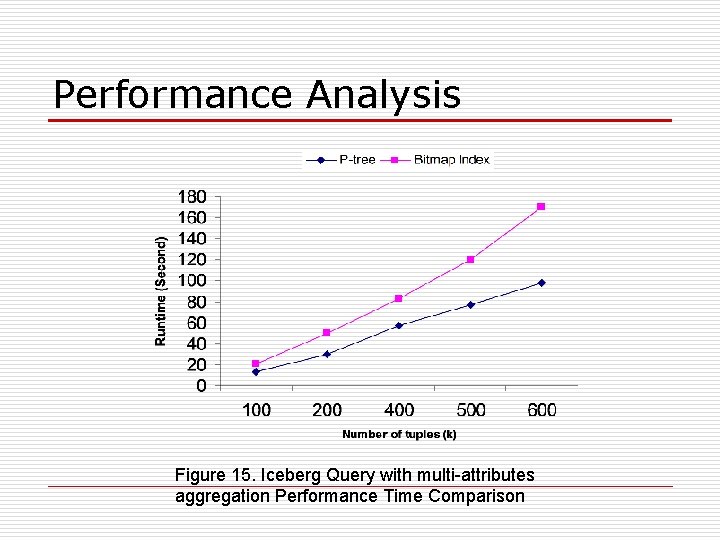
Performance Analysis Figure 15. Iceberg Query with multi-attributes aggregation Performance Time Comparison

Performance Analysis o o Our experiments are implemented in the C++ language on a 1 GHz Pentium PC machine with 1 GB main memory running on Red Hat Linux. In figure 15, we compare the running time of P -tree method and bitmap method on calculating multi-attribute iceberg query. In this case Ptrees are proved to be substantially faster.

Conclusion o o we believe our study confirms that the P-tree approach is superior to the bitmap approach for aggregation of all types and multi-attribute iceberg queries. It also proves that the advantages of basic P-tree representations of files are: n n First, there is no need for redundant, auxiliary structures. Second basic P-trees are good at calculating multiattribute aggregations, numeric value, and fair to all attributes.